Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью.

В4.3 изложен общий способ построения линии пересече­ния двух плоскостей с помощью вспомогательных секущих плос­костей (см. рис. 4.11). Но для построения линии пересечения двух плоскостей общего положения можно использовать точки пересечения двух прямых, принадлежащих одной из плоско­стей, с другой плоскостью. Построение же точек пересечения прямой линии с плоскостью общего положения изложено в 4.2.

Например (рис. 4.12), одна из плоскостей задана пересека­ющимися прямыми AB и АС. Для построения линии пересече­ния ее с плоскостью Q строят точки М и N пересечения прямых AB и АС с этой плоскостью и через них проводят линию MN пересечения двух заданных плоскостей.

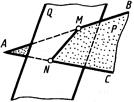
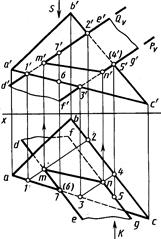
Рис. 4.12 Рис. 4.13

Таким образом, для построения линии пересечения плоско­стей строят точки пересечения прямых одной плоскости с другой и через них проводят искомую линию.

Пример такого построения на чертеже приведен на рисун­ке 4.13. Одна из плоскостей задана треугольником с проекциями a'b'c', abc.Вторая – параллельными прямыми с проекциями d'e', de и fg', fg.

Для построения проекций линии пересечения определены проекции m',m и n', n двух ее точек пересечения прямых с проекциями d'e', de и f'g', fg с плоскостью треугольника. Про­екции m', m, n', n точек пересечения построены с помощью фронтально-проецирующих плоскостей, заданных следами Q_v и P_v.Плоскость Q проходит через прямую DE и пересекает плоскость треугольника по линии с проекциями 1'–2', 1–2.Пере­сечение горизонтальных проекций 1–2 и de является горизонталь­ной проекцией m искомой точки. По ней построена фронтальная про­екция т' на фронтальной проек­ции d'e'.

Аналогично с помощью плос­кости P (P_v) построены проекции n', n второй точки. Через пост­роенные проекции m', n' и m, n проведены проекции m'n', mn отрезка, по которому пересекают­ся заданные пластины.

Анализ видимости участков пластин на фронтальной проек­ции выполнен с помощью точек с проекциями 4', 4 и 5', 5, ле­жащих на скрещивающихся пря­мых с проекциями b'c', bc и g'f', gf.Их фронтальные проекции 4' и 5' совпадают. На горизонтальной проекции вид­но, что при взгляде по стрелке К точка S закрывает точку 4.Видимость участков пластин на горизонтальной проекции оп­ределена с помощью точек с проекциями 6', 6 и 7', 7, лежа­щих на скрещивающихся прямых с проекциями a'c', ас и d'e', de.Их горизонтальные проекции 6 и 7 совпадают. Из фронтальной проекции видно, что при взгляде по стрелке S точ­ка 7 закрывает точку 6.

Построение взаимно параллельных прямой линии и плоскости, двух плоскостей.

17.Построение взаимно параллельных прямой линии и плос­кости, двух плоскостей.

Известно, что если прямая линия (AB,рис. 4.14) параллельна прямой KL,лежащей в плоскости, то она па­раллельна этой плоскости.

Для построения прямой, проходящей через заданную точку про­странства параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой, принадлежащей плоскости.

При этом возможно бесчисленное множество решений. Допол­нительные требования могут обусловить единственное решение.

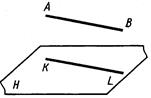
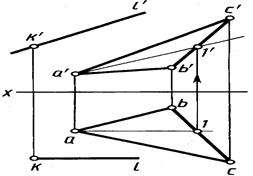
Рис. 4.14 Рис.4.15

В качестве примера на рисунке 4.15 показано построение проекций прямой линии, проходящей через точку с проекци­ями k', k,параллельной плоскости треугольника с проекция­ми a'b'c', abc и параллельной плоскости V – дополнительное требование. В плоскос-ти треугольника проведена фронталь с проекциями а'1', а –1.Проекции искомой прямой проведе­ны через проекции k', k точки параллельно проекциям фронтали k'l'║ а'1', kl║а–1.

Для того чтобы проверить, параллельна ли прямая задан­ной плоскости, можно попробовать провести в этой плоскости прямую, параллельную заданной. Если такую прямую в плос­кости построить не удается, то заданные прямая и плоскость не параллельны между собой. Можно также попытаться найти точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плос­кость взаимно параллельны.

Построение взаимно параллельных плоскостей.Для такого построения ис­пользуют известное свойство: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пе­ресекающимся прямым другой плоско­сти, то плоскости параллельны.Так, например, на рисунке 4.16, а построе­на плоскость, проходящая через точ­ку с проекциями k', k, параллельная плоскости, заданной проекциями a'b' ab и a'c', ас пересекающихся прямых. Для этого через фронтальную проекцию k' проведены фронтальные проекции d'k' || a'c', e'k' || а'b' и че­рез горизонтальную проекцию k – горизонтальные проекции dk || ас, ek || ab.Построенная плоскость, оп­ределяемая проекциями k'd', k'e' и kd, ke, будет параллельна заданной плоскости.

Построение параллельных плоскостей на чертеже удобно выполнять с помощью главных линий плоскости – горизонталей и фронталей. На рисунке 4.16, б плоскость P задана проекциями a'b', c'd' и ab, cd параллельных прямых. Параллельная ей плоскость T должна проходить через точку с проекциями k', k.Проекции плоскости T построены с помощью фронтальных проекций k'f' фронтали и k'g' горизонтали и горизонтальных проекций kg горизонтали и kf фронтали. При этом k'f' || 1'3', kg || 1–2.

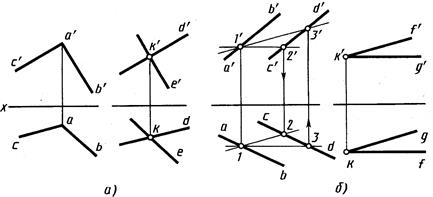
Рис.4.16