Проверка гипотезы о значимости коэффициента регрессии.

1. Определяем гипотезы H₀ и H₁:

H₀: 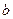=0 (между величинами нет линейной зависимости),

H₁: 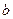≠0.

2. Зададим уровень значимости 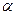=0,05.

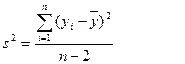
3. 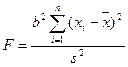Статистика критерия.

, где

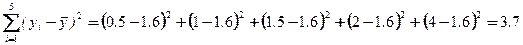
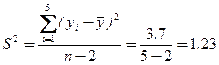
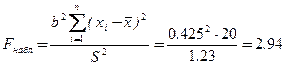
4. Критические точки и критическая область. Статистика F имеет распределение Фишера с 1 и (n-2) степенями свободы. F_α,1,n-2. .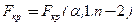

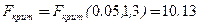
5. 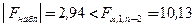, то H₀ отвергается, т.е. можно сделать вывод, что линейная зависимость значима.

2) график

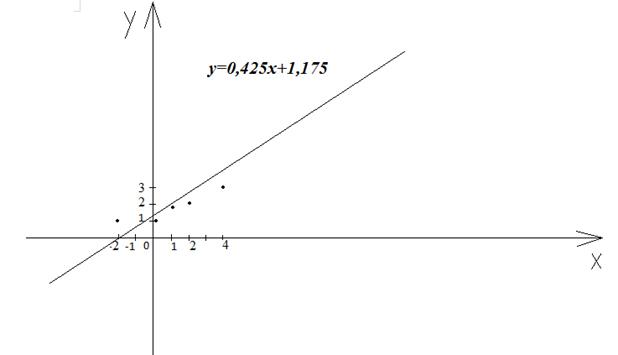
3) Выборочный коэффициент корреляции

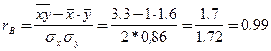
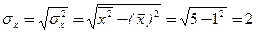
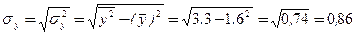
или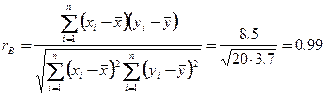

4) Так как 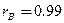, то корреляционная связь по своему характеру прямая,а по силе – сильная.

Проверка гипотезы о значимости коэффициента корреляции.

1. Сформулируем гипотезы H₀ и H₁:

H₀: r =0 (корреляции нет),

H₁: r ≠0.

2. Зададим уровень значимости α=0,05.

3. Статистика критерия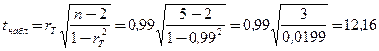

4. 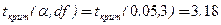-t-статистика, имеющая распределение Стьюдента с (n-2) степенями свободы.

6. 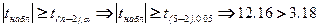, то H₀ отвергается. Это значит, что между параметрами существует значимая корреляция.

ЗАДАЧА

на применение рангового метода

Задание: методом корреляции рангов установить направление и силу связи между стажем работы в годах и числом травм, если получены следующие данные:

Стаж работы в годах	Число травм
До 1 года
1-2
3-4
5-6
7 и более

Обоснования выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, так как первый ряд признака «стаж работы в годах» имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод - метод квадратов.

РЕШЕНИЕ ЗАДАЧИ

Стаж работы в годах	Число травм	Порядковые номера (ранги)	Разность рангов	Квадрат разности рангов
x	y	d=x-y	d2
До 1 года				-4
1-2				-2
3-4			2,5	0,5	0,25
5-6			2,5	1,5	2,25
7 и более
					Σd2 = 38,5

Произведем расчет коэффициента ранговой корреляции по формуле:

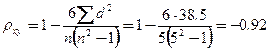
Определим достоверность коэффициента ранговой корреляции.

1-й способ. Определить ошибку (mρxy) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:

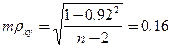
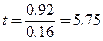
Полученный критерий t = 5,75 соответствует вероятности безошибочного прогноза (р) больше 99,9%.

ρ_xy = - 0,92 ; mρ_xy = ±0,16 ; t = 5,75 ; р> 99,9 %

2-й способ. По таблице «Стандартных коэффициентов корреляции»: при числе степеней свободы (n — 2) = 5 — 2 = 3 наш расчетный коэффициент корреляции ρxy = –0,92 больше табличного 0,878 и меньше 0,933, что соответствует вероятности безошибочного прогноза больше 95% и меньше 98%. Это позволяет считать полученный коэффициент ранговой корреляции достоверным.

Вывод: с вероятностью безошибочного прогноза (р) больше 95% установлена обратная, сильнаякорреляционная связь между стажем работы и числом травм, т.е. чем меньше стаж работы, тем больше травм.

Задания.

1. Даны показатели охвата населения прививками Х (%) и заболеваемости брюшным тифом 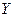(в %).

Районы	A	B	C	D	E	F	G	H	I
X	14,7	13,4	9,6	8,1	5,5	5,2	4,4	4,4	4,0
Y	1,4	1,4	2,3	2,1	6,2	6,9	8,6	10,8	11,0

Проведите корреляционно-регрессионный анализ полученных данных.