ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ № 1
Вариант 1.
1. Найти производные функций
А)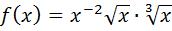 
Б)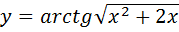 
2. Составить уравнения касательной к кривой
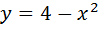в точке с абсциссой x=-1
Выполнить чертеж.
3. А) Найти следующий интеграл
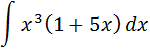
Б) Вычислить определённый интеграл
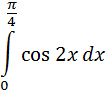
4. Найти общие решения уравнения
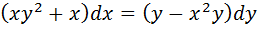
5. А) Вычислить:
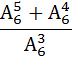
Б) Группа учащихся изучает 8 различных дисциплин. Сколькими способами можно составить расписание занятий в субботу, если в этот день недели должно быть три различных урока?
Вариант 2.
1. Найти производные функций
А)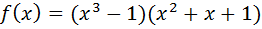 
Б)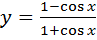 
2. Найти дифференциал следующей функции
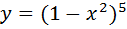
3. А) Найти следующий интеграл
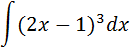
Б) Вычислить определённый интеграл
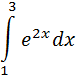
4. Найти общие решения уравнения
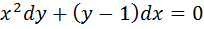
5. А) Вычислить:
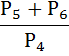
Б) Сколькими способами восемь различных книг можно расставить на одной полке так чтобы две определённые книги оказались рядом.
Вариант 3.
1. Найти производные функций
А)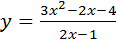 
Б)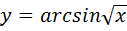 
2. Тело движется прямолинейно по закону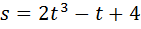 
. Найти скорость тела в моменты t1=0, t2=2.
3. А) Найти следующий интеграл
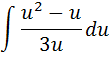
Б) Вычислить определённый интеграл
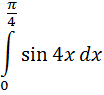
4. Найти общие решения уравнения
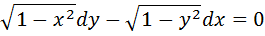
5. А) Вычислить:
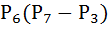
Б) Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, не повторяя цифр в числе?
Вариант 4.
1. Найти производные функций
А)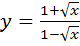 
Б)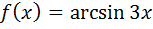 
Найти значение производной функции
при х=0.
2. Найти скорость движения тела в момент времени t=2, если закон движения задан формулой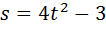 
.
3. А) Найти следующий интеграл
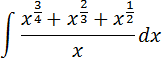
Б) Вычислить определённый интеграл
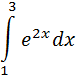
4. Найти общие решения уравнения
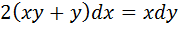
5. А) Вычислить:
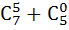
Б) В урне 10 белых и 5 чёрных шаров. Сколькими способами из урны можно вынимать наугад 3 шара, чтобы:
1) все три шара оказались белыми;
2) два шара оказались белыми, а один чёрным ?
Вариант 5.
1. Найти производные функций
А)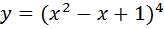 
Б)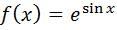 
2. 
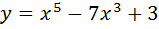Найти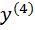 
3. А) Найти следующий интеграл
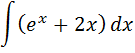
Б) Вычислить определённый интеграл
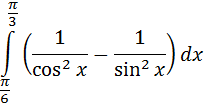
4. Найти общие решения уравнения
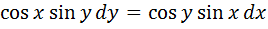
5. А) Вычислить:
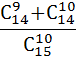
Б)В розыгрыше личного первенства техникума по шахматам было сыграно 120 игр. Сколько было участников, если каждые два участника встречались между собой один раз?
Вариант 6.
1. Найти производные функций
А)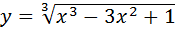 
Б)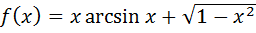 
2. Исследовать на монотонность и экстремумы функцию:
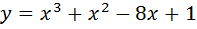
3. А) Найти следующий интеграл
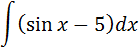
Б) Вычислить определённый интеграл
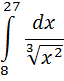
4. Найти частные решения уравнения
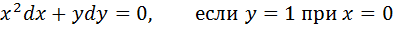
5. А) Найти n, если:
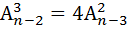
Б) В группе 20 юношей и 10 девушек. Сколькими способами можно избрать трёх юношей и двух девушек для участия в слёте студентов?
Вариант 7.
1. Найти производные функций
А)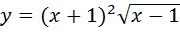 
Б)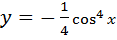 
2. Исследовать на монотонность и экстремумы функцию:
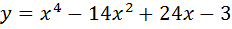
3. А) Найти следующий интеграл
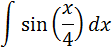
Б) Вычислить площадь фигуры, ограниченной линиями:
у=9-х2 и у=0.
Выполнить чертеж.
4. Найти частные решения уравнения
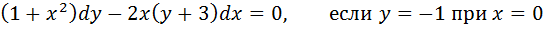
5. А) Найти n, если:
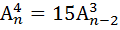
Б) В урне 9 белых и 6 чёрных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
Вариант 8.
1. Найти производные функций
А)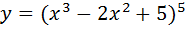 
Б)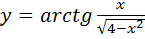 
2. Найти наименьшее и наибольшее значения следующей функции:
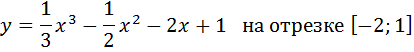
3. А) Найти следующий интеграл
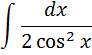
Б) Вычислить площадь фигуры, ограниченной линиями:
у=0,25х2 и у= -0,5х2+3х
Выполнить чертеж.
4. Найти частные решения уравнения
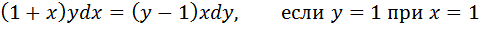
5. А) Найти n, если:
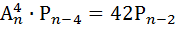
Б) В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что среди пяти взятых наугад деталей ровно три стандартных.
Вариант 9.
1. Найти производные функций
А)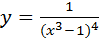 
Б)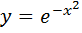 
2. Найти наименьшее и наибольшее значения следующей функции:
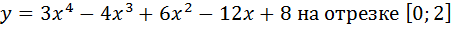
3. А) Найти следующий интеграл
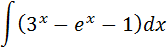
Б) Вычислить площадь фигуры, ограниченной линиями:
у= -х2+6 и у=2х+3
Выполнить чертеж.
4. Найти частные решения уравнения
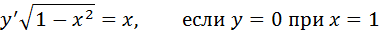
5. А) Найти n, если:
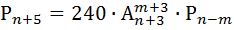
Б) Восемь различных книг расставляют наугад на одной полке. Найти вероятность того, что две определённые книги окажутся поставленными рядом.
Вариант 10.
1.Найти производные функций
А)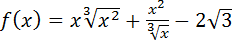 
Б)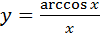 
2.Составить уравнения касательной к кривой
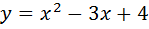в точке с абсциссой x=1
Выполнить чертеж.
3.А)Найти следующий интеграл
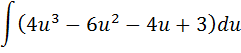
Б) Вычислить определённый интеграл
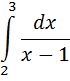
4.Найти общие решения уравнения
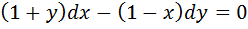
5.А) Вычислить:
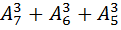
Б) Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что в каждом числе нет одинаковых цифр?
ДЕМО - вариант итоговой письменной контрольной работы
(классной)
-
СОДЕРЖАНИЕ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
Вопросы для подготовки к дифференцированному зачету
1. Функции одной независимой переменной. Способы задания функции. Пределы.
2. Непрерывность функций. Асимптоты кривой.
3. Определение производной.
4. Таблица основных формул дифференцирования. Правила дифференцирования. Практические задания.
5. Механический смысл производной. Практические задания.
6. Геометрический смысл производной. Уравнение касательной к графику функции. Практические задания.
7. Монотонность функции. Признаки возрастания и убывания функции. Практические задания.
8. Экстремумы функции. Достаточные условия существования экстремума. Практические задания.
9. Выпуклость графика функции. Точки перегиба.
10. Общая схема исследования функций. Практические задания.
11. Дифференциал функции. Практические задания.
12. Первообразная функции. Неопределенный интеграл. Таблица основных интегралов. Свойства
13. неопределенного интеграла. Практические задания.
14. Методы интегрирования.
15. Определенный интеграл. Геометрический смысл определенного интеграла. Формула Ньютона- Лейбница. Свойства определенного интеграла. Практические задания.
16. Применение определенного интеграла. Практические задания.
17. Дифференциальные уравнения 1 порядка. Практические задания.
18. Дифференциальные уравнения 2 порядка. Практические задания.
19. Числовые ряды. Сходимость и расходимость числовых рядов. Практические задания.
20. Знакопеременные ряды.
21. Степенные ряды.
22. Множество и его элементы. Пустое множество, подмножество.
23. Операции над множествами. Числовые множества. Практические задания.
24. Определение графа, виды графов. Элементы графа.
25. Связанные графы. Ориентированный граф.
26. Понятие события и вероятности события. Достоверные и невозможные события.
27. Элементы комбинаторики. Размещения. Практические задания.
28. .Сочетания. Практические задания.
29. Перестановки. Практические задания.
30. Классическое определение вероятности. Практические задания.
31. Теоремы сложения и умножения вероятности. Практические задания.
32. Случайная величина, ее характеристики.
33. Понятие о численном дифференцировании.
34. Понятие о численном интегрировании.