Частные случаи нормального закона распределения. 4 страница

	X						Y
P	0,2	0,2	0,5	0,1		P	0,1	0,5	0,3	0,1

	X						Y
P	0,2	0,4	0,3	0,1		P	0,1	0,5	0,2	0,2

	X						Y
P	0,1	0,2	0,5	0,2		P	0,1	0,4	0,2	0,3

	X						Y
P	0,1	0,3	0,4	0,2		P	0,2	0,4	0,3	0,1

	X						Y
P	0,2	0,3	0,1	0,4		P	0,2	0,3	0,4	0,1

	X						Y
P	0,2	0,3	0,1	0,4		P	0,2	0,1	0,5	0,2

	X						Y
P	0,1	0,2	0,4	0,3		P	0,2	0,3	0,4	0,1

	X						Y
P	0,3	0,5	0,1	0,1		P	0,1	0,4	0,3	0,2

	X						Y
P	0,1	0,2	0,2	0,5		P	0,1	0,3	0,2	0,4

ЗАДАЧА 11 (№ 1–10)

Пусть всхожесть семян ржи составляет а%. Случайная величина Х – количество взошедших семян ржи из п посеянных семян. Составить закон распределения случайной величины Х, построить полигон распределения и вычислить его числовые характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение.

(№ 11-20)

В среднем по а% договоров страховая компания выплачивает страховую сумму. Случайная величина Х – число договоров, связанных с выплатой страховой суммы из п рассмотренных договоров с наступлением страхового случая. Составить закон распределения случайной величины Х, построить полигон распределения и вычислить его числовые характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение.

(№ 21-40)

Пусть а% изделий данного предприятия – это продукция высшего сорта. Некто приобрел п изделий, изготовленных на этом предприятии. Случайная величина Х – число изделий высшего сорта из п приобретенных изделий. Составить закон распределения случайной величины Х, построить полигон распределения и вычислить его числовые характеристики: математическое ожидание, дисперсию и среднее квадратическое отклонение.

№	а	п		№	а	п

Решение типового примера. Заданы законы распределения двух случайных величин и .

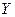X	–5
P	0,5	0,3	0,1	0,2

Y
P	0,2	0,8

Найти математическое ожидание и дисперсию для случайной величины

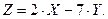
Решение. Найдем математические ожидания и дисперсию для случайных величин и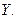

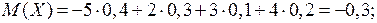
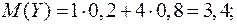
Напишем законы распределения для случайных величин 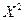и :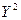

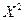P	0,4	0,3	0,1	0,2

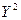P	0,2	0,8

Найдем математическое ожидание для случайных величин 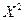и :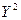

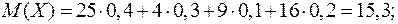
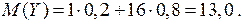
Отсюда,

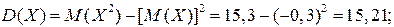
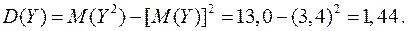
Наконец, пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин и 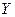, получаем:

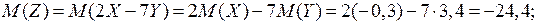
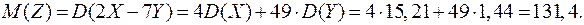
ЗАДАЧА 12

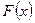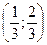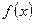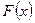Случайная величина задана функцией распределения вероятностей .Найти: 1) вероятность попадания случайной величины в интервал ; 2) плотность распределения вероятностей случайной величины (т.е ); 3) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины ; 4) Построить графики функций и .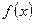

1.

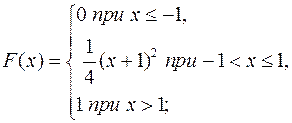
2.

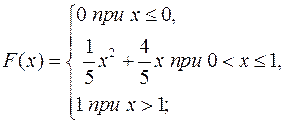
3.

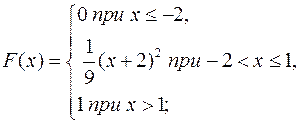
4.

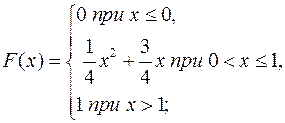
5.

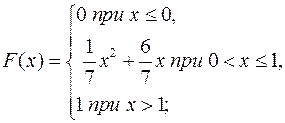
6.

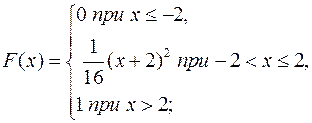
7.

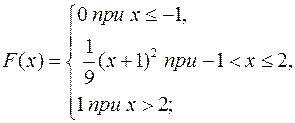
8.

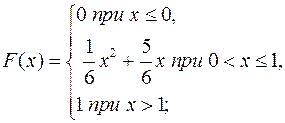
9.

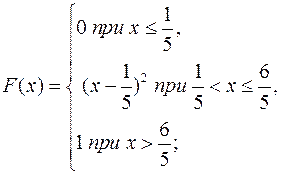
10.

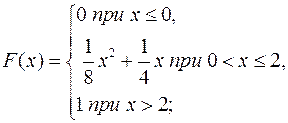
11.

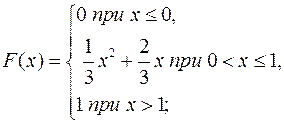
12.

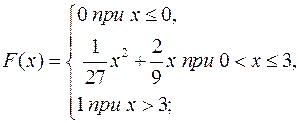
13.

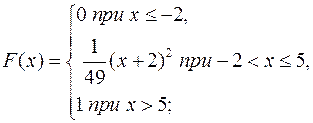
14.

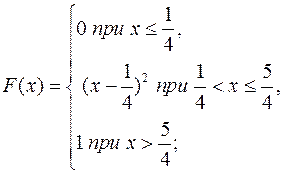
15.

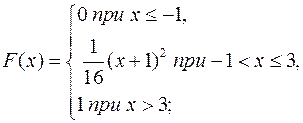
16.

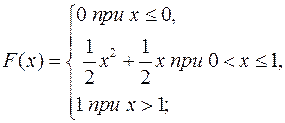
17.

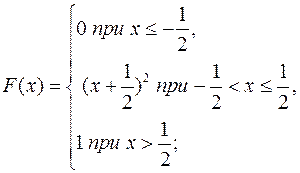
18.

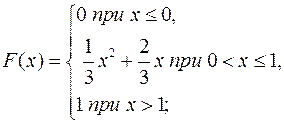
19.

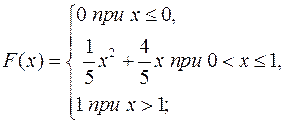
20.

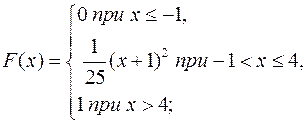
21.

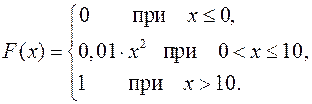
22.

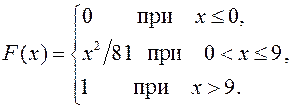
23.

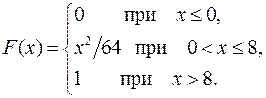
24.

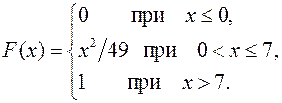
25.

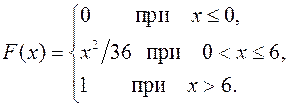
26.

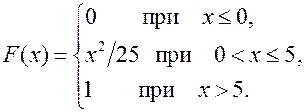
27.

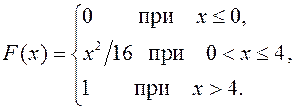
28.

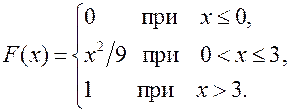
29.

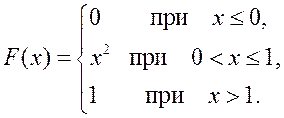
30.

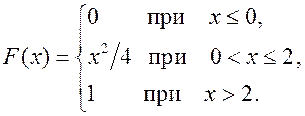
31.

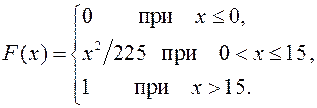
32.

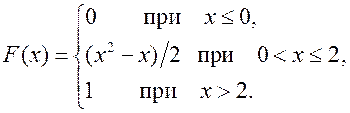
33.

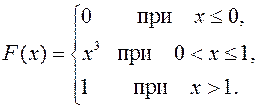
34.

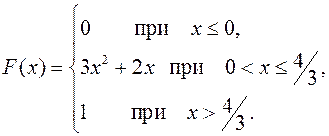
35.

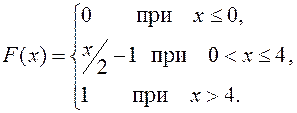
36.

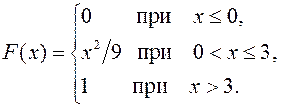
37.

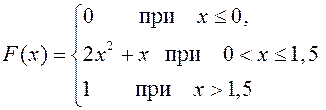
38.

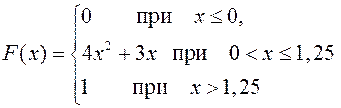
39.

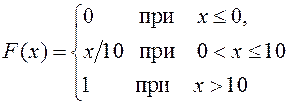
40.

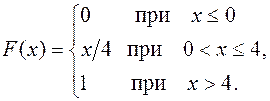
Решение типового примера.Случайная величина задана функцией распределения вероятностей

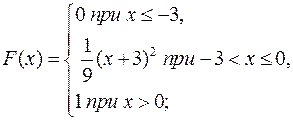
Найти: 1) вероятность попадания случайной величины в интервал ;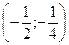
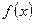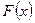2) плотность распределения вероятностей случайной величины (т.е ); 3) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины ; 4) Построить графики функций и .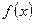

Решение. 1) Вероятность того, что случайная величина примет значение, заключенное в интервале 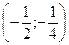, равна приращению функции распределения на этом интервале:

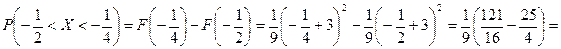
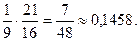
2) Найдем плотность распределения вероятностей случайной величины по формуле

.

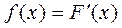Получаем

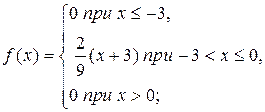
3) Математическое ожидание случайной величины находим по формуле

.

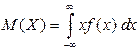Имеем

.

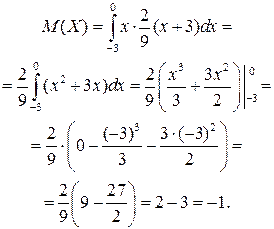Дисперсию находим по формуле

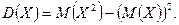
Имеем

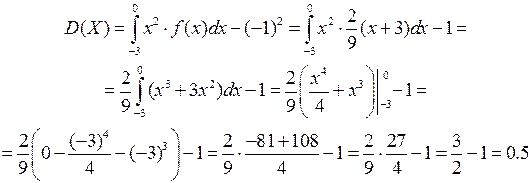
Отсюда .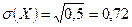

4) Построим график функции .

x	-4	-3	-2	-1
F(x)	0,1		0,1	0,44

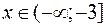при – графиком является часть прямой, совпадающая с осью абсцисс (рис. 1).

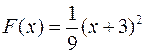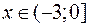при – графиком является часть параболы, с вершиной в точке (-3; 0).

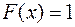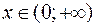при – графиком является часть прямой, параллельная оси абсцисс.

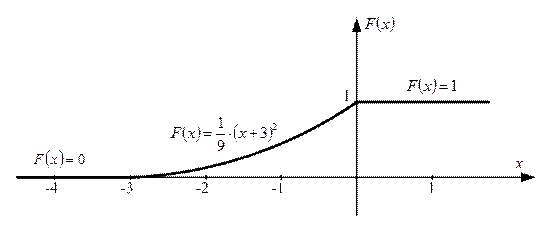
Рис. 1

Построим график функции плотности .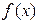

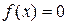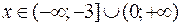при – графиком является часть прямой, совпадающей с осью абсцисс (рис. 2). 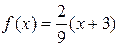при 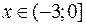– графиком является часть прямой .

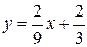x	-3
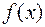		0.66

Рис. 2

Литература

1. Кремер, Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер. - М.: ЮНИТИ, 2001, - 543 с.

2. Зайцев, И.А. Высшая математика / И.А. Зайцев. - М.: Высш. шк., 1998. – 409 с.

3. Созутов, А.И. Теория вероятностей / А.И. Созутов, В.П. Сакулин. - Красноярск: Изд-во КрасГАСА 2001. - 74 с.

4. Чубарев, А.М. Невероятная вероятность / А.М. Чубарев, В.С. Холодный. - М.: Знание, 1976. - 126 с.

5. Федорова, Е.Н. Теория вероятностей. Обучающая и контролирующая программа по теме «Нормальное распределение» / Е.Н. Федорова. - М.: Изд-во ВСХИЗО, 1988. - 31 с.

6. Федорова, Е.Н. Высшая математика. Обучающая и контролирующая программа по теме «Биноминальное распределение» / Е.Н. Федорова. - М.: Изд-во ВСХИЗО, 1990. - 27 с.

7. Федорова, Е.Н. Высшая математика. Обучающая и контролирующая программа по теме «Приближенные формулы биноминального распределения» / Е.Н. Федорова. - М.: Изд-во ВСХИЗО, 1991. - 26 с.

8. Малышева, О.Г. Основы теории вероятностей / О.Г. Малышева. - Красноярск: Изд-во КрасГАУ, 1998. - 64 с.

9. Раскин, В.Г. Высшая математика и математические модели в расчетах на ЭВМ / В.Г. Раскин, С.Н. Дементьев. - М.: Изд-во ВСХИЗО, 1990. - 124 с.

10. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. - М.: Высш. шк., 2001. - 400 с.

11. Гурский, Е.И. Теория вероятностей с элементами математической статистики / Е.И. Гурский. - М.: Высш. шк., 1971. - 328 с.