Постановка задачи интерполирования. Существование и единственность ОИМ

Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.

В вычислительной математике, как правило, рассматривается реш. корректно поставленных задач. Это значит, что исходная задача имеет ! реш., кот. в некоторой обл. непрерывно зависит от исходных данных задачи. На практике значения почти всех величин задаются и определяются приближенно. Из-за этого получается погрешность. Провести реш. задачи нужно так, чтобы погрешность полученного реш. не превышала допустимую.

При этом заданы значения угла и гипотенузы , полученные в результате измерения. Точные знач. исходных величин обозначим соответственно и . Таким образом, точное значение площади выражается формулой

Знач. площади через заданные знач. исходных величин определ. выражением . Разность наз. неустранимой погрешн. Эта погрешн. обусловлена неточным заданием исходных данных. Для вычисления значений тригонометр. функций воспользуемся их разложен. в ряд Тэйлора, тогда придем к равенству Разность наз. погрешн. метода. Погрешн. метода можно сделать достаточно малой. В нашем примере математику для этого нужно взять в разложениях достаточно большое значение . Фактически вычисленное знач. площади обозначим . Разность наз. вычислительной погрешн. Уменьшить вычислит. погрешн. можно за счет использования ЭВМ с большей разрядной сеткой, а также за счет программирования операций над числами с большой разрядностью. Полная погрешн. складыв. из трех указанных видов погрешн.: .

Неустраним. погрешность. Обозначим – приближ. знач. величины, - ее точное знач. Погрешн. приближ. величины опред. равенством .

Абсолют. погрешн. определяется неравенством .

Величину наз. относительной погрешн. приближ. числа . Если , то в качестве относител. погрешн. можно взять число .

Значащими цифрами числа наз. все его ненулевые цифры и нули, кот. находятся между значащими цифрами или явл. представителями сохраненного десятичного разряда.

Значащая цифра приближ. числа наз. верной, если абсолют. погрешн. числа не превосходит половины единицы разряда, в котором эта цифра находится.

Зам.Абсолют. и относит. погрешн. записывают с точностью до одной или двух значащих цифр.

Зам.. Абсолют. и относит. погрешности округляют только с избытком.

Постановка задачи интерполирования. Существование и единственность ОИМ.

Интерполиров. или интерпол. – один из наиболее часто применяемых на практике методов приближ. ф. Задача интерполиров. ставится след. образом.

Рассм. пр. и фун. , определ. на отр[a;b]. Задана последов. линейно независимых ф. . Образуем линейную комбинацию (1)

Линейную комбинацию вида (1) наз. ОМ(обобщ. многоч) по сист. ф. .

Сист. ф. наз. сист. Чебышева на отр. 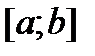, если любой нетривиальный ОМ по этой сист. обращается в нуль на отр. 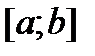не более чем в n точках.

В задаче интерполиров. ф. нужно приблизить ОМ (1) так, чтобы знач. ф. и ОМ совпадали в задан. точках: .(2)

ОМ , удовлетв. условиям (2), наз. ИОМ. При этом ф. 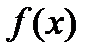, для кот. строится ИОМ., наз. интерполир. ф., а точки наз. узлами интерполяции. Равенства (2) будем наз. интерполяц. условиями.

Теорема и ! ИОМ. Для того чтобы для ф. при наборах попарно неравных узлов существ. ИОМ. по сист. ф. , необх. и достат., чтобы эта сист. ф. была сист. Чебышева на отр. . При этом ИОМ будет единственным.

ИМ Лагранжа.

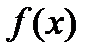Сист. ф. , (1) в силу основн. теоремы алгебры, явл. сист. Чебышева на любом отр. Для любой ф. по этой сист. ф. при любом наборе попарно неравных узлов ! ИОМ, кот. может быть записан в виде (2) где ОМ не зависят от ф. .Зафикс. j и рассм. ф. , приним. в узлах значения Для этой ф. имеем ИОМ . Т.к. выполн. интерполяц. услов., то . Т.о., для ОМ имеет место свойств. (3) Если построить ОМ , удовл. свойств. (3), то тем самым будет построен ИОМ (2). Для сист. ф. (1),очевидно, многочл. облад. свойств. (3). Т.о., по сист. ф. (3) ИМ получается в виде (4). (4) наз. ИМ Лагранжа для ф. 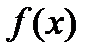по . Обозн. имеем и .С использ. многочл. ИМ Лагранжа примет вид .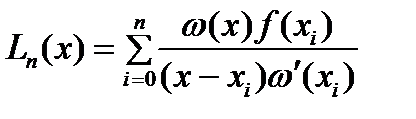

Схема Эйткина

Обозначим через интерполяционный многочлен, построенный для функции по узлам

В схеме Эйткена сначала для заданного значения аргумента выбирается ближайший табличный узел среди всех табличных узлов Пусть это будет табличный узел . Этот табличный узел берется в качестве узла интерполяции . Соответствующее табличное значение функции обозначим через . Это табличное значение можно считать начальным приближением к искомому значению функции в точке .

Далее из оставшихся табличных узлов снова выбирается ближайший к . Это будет или или Найденный очередной ближайший узел обозначается ,а соответствующее табличное значение обозначается Затем проводятся вычисления по формуле (2) Здесь в числителе дроби находится определитель квадратной матрицы второго порядка.

Определяемый формулой (2) многочлен имеет первую степень и является интерполяционным для с узлами интерполяции и .

Проверьте самостоятельно, что действительно выполняются условия интерполяции .

Будем считать тождественными обозначения и Тогда формула (2) может быть переписана в виде

.

Вычисленное значение является вторым приближением к искомому значению . Это значение получается линейной интерполяцией по формуле (2).

На следующем шаге схемы Эйткена из оставшихся табличных узлов находится ближайший к заданному значению и обозначается через (берется в качестве) . Новое приближение к искомому значению вычисляется по формуле

(3)

Перед этим предварительно должно быть вычислено , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции , .

Докажите самостоятельно, что для многочлена второй степени , определяемого формулой (3) выполняются интерполяционные условия

, , .

Если значения и совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение .

В противном случае выбирается еще один узел интерполяции и проводятся вычисления по формуле (4)при i=3 и =1,2,3.

Формула (4) является основной вычислительной формулой схемы Эйткена. Формула (2) получается из нее при i=k=1. Формула (3) получается из (4) при i=k=2.