Задачи на увеличение числа на несколько единиц
Математика
1.Вычитание— это действие, обратное сложению.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Результат вычитания называют разностью.
Законы сложения
Переместительный закон сложения
От перемены мест слагаемых значение суммы не меняется.
a + b = b + a (4 + 2 = 2 + 4)
Сочетательный закон сложения
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
3.Умножение— это сложение одинаковых слагаемых.
2 + 2 + 2 = 2 · 3 = 6
2 — слагаемое;
3 — число, которое показывает, сколько раз повторяется слагаемое 2.
Особые случаи умножения
a ∙ 1 = a 1 ∙ a = a 0 ∙ a = 0 a ∙ 0 = 0
4 ∙ 1 = 4 1 ∙ 4 = 4 0 ∙ 6 = 0 6 ∙ 0 = 0
Законы умножения
Переместительный закон умножения
От перестановки множителей произведение не меняется.
a · b = b · a 2 · 5 = 5 · 2
Сочетательный закон умножения
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. (a · b) · c = a · (b · c) = (a · c) · b
(2 · 5) · 3 = 2 · (5 · 3) = (2 · 3) · 5
Распределительный закон умноженияотносительно сложения
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) · d = a · d + b · d + c · d
Относительно вычитания
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
(a – b) · c = a · c – b · c
4.Деление— это действие, обратное умножению.
6:2=3 делимое делитель частное
Особые случаи деления
a : 1 = a 0 : a = 0 a : a = 1
8 : 1 = 8 0 : 8 = 0 8 : 8 = 1
На нуль делить нельзя!
Свойства деления
Чтобы разделить сумму на число,достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
(a + b) : c = a : c + b : c
Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.
(a – b) : c = a : c – b : c
Частное от деления произведения двух множителей на числоравно произведению одного из множителей на частное от деления второго множителя на это число.
(a · b) : c = (a : c) · b = a · (b : c)
Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.
a : (b : c) = (a : b) · c
Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат. Можно так же разделить делимое на это число, а полученный результат разделить на делитель.
(a : b) : c = a : (b · c) или (a : b) : c = (a : c) : b
5.Уравнения:
5.1.Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель
Х*3=6 х=6:3
5.2.Чтобы найти неизвестный делитель, нужно делимое разделить на частное. 6 : х= 2 х= 6 : 2
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
х: 2 = 3 х= 3 · 2
5.3.Чтобы найти неизвестное слагаемое, надо из суммы вычесть другое слагаемое
Х+2=6 х=6-2
5.4.Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое
Х-2=6 х=6+2
5.5.Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
3+х=9 х=9-3
5.6.Правило оформления уравнения:
6 : х = 2
х = 6 : 2
х=3
6:3=2
Ответ: х=3
Единицы измерения
Единицы измерения длины
1 см = 10 мм
1 дм = 10 см
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м = 10 000 дм = 100 000 см
Единицы измерения массы
1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг
Единицы измерения времени
1 мин = 60 с 1 ч = 60 мин = 3600 с
1 сутки = 24 часа
1 неделя = 7 дней
1 месяц = 30 или 31 день(в феврале 28 или 29 дней)
1 год = 12 месяцев = 52 недели = 365 или 366 дней
1 век (столетие) = 100 лет
Порядок действий в выражениях
7.1.В выражениях без скобок, где выполняются только сложениеи вычитание, действия выполняют в том порядке, в котором они записаны (то есть слева направо).
1 2
70 – 26 + 10 = 54
7.2.В выражениях без скобок, где выполняются только умножениеи деление, действия выполняют в том порядке, в котором они записаны.
1 2
36 : 9 · 3 = 12
7.3.В выражениях со скобкамипервым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание.
2 1
80 – (46 – 14) = 48
2 1
6 · (30 – 20) = 60
2 1
90 : (2 · 5) = 9
7.4.В выражениях, где есть действия первой и второй ступеней (то есть +, –,·, :), сначала выполняются по порядку умножение и деление, а затем по порядку сложение и вычитание.
1 3 1
6 · 5 + 40 : 2 = 50
2 1 3
72 – 24 : 6 + 2 = 70
Задачи
8.1.Задачи на нахождение суммы двух чисел 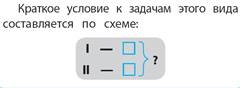 | 8.2.Задачи на нахождение остатка 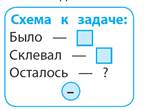 |
Задачи на увеличение числа на несколько единиц