Решить размерную цепь – рассчитать параметры составляющих звеньев так, чтобы при сборке обеспечить заданные параметры замыкающего звена.

Размер замыкающего звена обеспечивается за счет размеров и предельных отклонений составляющих звеньев.

АD

А1 А2

А1 А2

А3

А3

Геометрическая схема размерной цепи (размеры представлены в виде векторов одного направления):

АΔ

Если при увеличении размеров составляющих звеньев: 1. Замыкающее звено увеличивается, составляющие звенья называются увеличивающими; (А3) 2. Замыкающее звено уменьшается, составляющие звенья называются уменьшающими; (А1, А2) 3.

Решить размерную цепь – рассчитать параметры составляющих звеньев так, чтобы при сборке обеспечить заданные параметры замыкающего звена.

Уравнения размерных цепей отражают зависимость между параметрами замыкающего звена и параметрами составляющих звеньев:

Уравнение номинальных размеров:

Согласно расположению размеров на схеме, А_Δ = А₃ – А₁ – А₂ , из уравнения следует: размеры со знаком плюс – увеличивающие, со знаком минус – уменьшающие, т.е. А_Δ = А_ув. – А_ум.

Передаточное отношение – ξ_i – коэффициент приведения составляющего звена на направление замыкающего звена.

Для линейных размерных цепе с параллельными звеньями передаточные отношения равны:

для увеличивающих составляющих звеньев ξ_i = +1;

для уменьшающих составляющих звеньев ξ_i = –1;

тогда окончательный вид уравнения номинальных размеров:

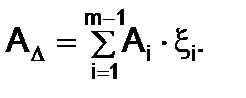(1)

Уравнение допусков (точности)

по методу max-min: по теоретико-вероятностному методу:

(метод полной взаимозаменяемости) (метод неполной взаимозаменяемости)

(2) 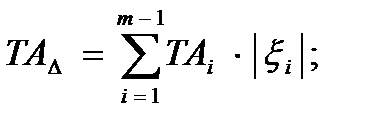(3)

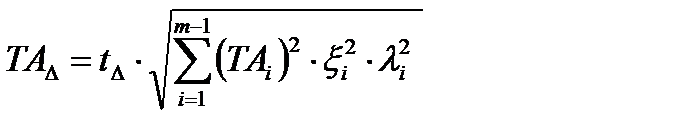
Уравнение координаты середины поля допуска:

по методу max-minи по теоретико-вероятностному методу:

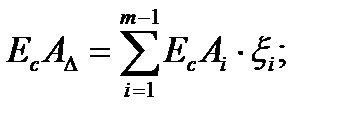(4)

Уравнения предельных отклонений замыкающего звена:

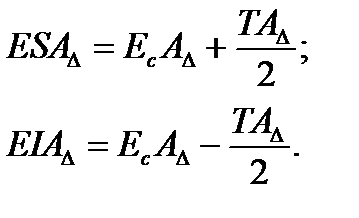(5)

Прямая задача – когда известны параметры замыкающего звена, необходимо найти параметры составляющих звеньев;

для решения прямой задачи в курсовой работе используется способ равных квалитетов.

Обратная задача – когда известны параметры составляющих звеньев, необходимо найти параметры замыкающего звена; для решения обратной задачи используются уравнения 1 – 5 .

С помощью уравнений размерных цепей производят все расчеты (в соответствии с поставленными задачами) параметров замыкающего и составляющих звеньев.

Существует два метода расчета параметров звеньев размерных цепей:

Метод максимума-минимума (используется при достижении точности размеров замыкающего звена методом полной взаимозаменяемости) и метод теоретико-вероятностный (используется при неполной взаимозаменяемости).

Вопросы для защиты курсовой:

1. Определения. Что называется: размерной цепью, замыкающим, исходным звеном, составляющими звеньями, увеличивающими, уменьшающими, специальными, компенсирующими звеньями.

Как обозначаются? Построение геометрической схемы р.ц.

2. Что значит – решить размерную цепь? Прямая, обратная задачи.

3. Основные параметры размерных цепей.

4. Методы расчета // р.ц. (2 метода), основные уравнения р.ц. для каждого метода расчета (5).

5. Физический смысл коэффициента риска (t_Δ), относительного средне-квадратического отклонения (λ_i)

6. Способы решения прямой задачи (2).

7. Методы достижения точности р.ц. (5 методов)

8. Уметь объяснить решение р.ц. в вашей курсовой, для любого из трех способов, указать где прямая и обратная задача.

9. Уметь объяснить назначение предельных отклонений на составляющие звенья после назначения на них допусков. В каждом из трех способов.