Упражнение. Измерение мощности рассеиваемой на различных нагрузках и определение характеристик цепи переменного тока
Порядок выполнения
1. Собрать цепь по схеме, изображенной на рис.4. В качестве источника переменного тока промышленной частоты использовать блок КОЛ-45 (гнезда 110 В подключать с помощью прилагающейся вилки с двумя наконечниками на другом конце). В качестве вольтметра взять цифровой прибор на пределе 1000 В по переменному току и амперметр с пределами на 2,5 и 5 А (прибор рекомендуется использовать на последнем пределе, и лишь тогда, когда токи в цепи меньше 2 А, использовать первый).
В качестве сопротивления r взять реостат, который при включении схемы должен быть ВВЕДЕН (сопротивление максимально), а при выполнении измерения – ПОЛНОСТЬЮ ВЫВЕДЕН. После окончания измерения его следует ВВЕСТИ СНОВА. Такая мера предостерегает приборы от порчи в момент включения напряжения в том случае, когда окажется нарушенной изоляция витков катушки индуктивности или диэлектрика конденсатора.
2. Выполните измерения Р, Iэфф и Uэфф для различных сопротивлений нагрузки Z, которые приведены в таблице 1.
Таблица 1.
| 1) | 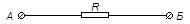 | Реостат без ползунка. |
| 2) | 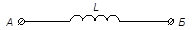 | Катушка индуктивности на 220 В, надетая на сердечник. |
| 3) | 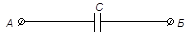 | Одна из возможных ёмкостей батареи конденсаторов. |
| 4) |  | Комбинации перечисленных сопротивлений нагрузки. |
| 5) |  | |
| 6) | 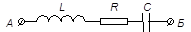 | |
| 7) |  |
Для удобства подключения и смены нагрузок Z рекомендуется использовать специальную панель, выводы которой подсоединять к точкам А и В схемы по рис.3.
ВНИМАНИЕ! Все переключения в схеме производить только под контролем преподавателя или лаборанта, выключив из сети КОЛ-45 .
3. Применив закон Ома для переменного тока, произведите соответствующие вычисления и запишите результаты в таблицу 2.
Таблица 2
| № схемы | компоненты | Iэфф А | Uэфф В | S ВА | P Вт | Q ВАр | cosj | Z Ом | R1 Ом | L Гн | С Ф |
ПРИМЕЧАНИЕ: Сильный ток (более 3 А) должен включаться на короткое время, т.к. нагревание катушки самоиндукции и реостата будет вызывать изменение их активных сопротивлений.
4. Используя в качестве нагрузки Z катушку школьного трансформатора на 220 В, изучить зависимость изменения cosj от глубины насадки железного сердечника, т.е. от величины индуктивного сопротивления цепи при включении в нее переменной индуктивности. Для этого следует сердечник школьного трансформатора положить на стол таким образом, чтобы стала видна миллиметровая шкала, укрепленная на нем, одеть на него катушку и произвести измерения мощности и cosj в том порядке, как написано в п.2. Затем следует сдвинуть катушку на 1 см вдоль сердечника и снова произвести измерение. Таким образом сделать 5...8 измерений. При нахождении катушки на краю сердечника ее следует слегка придерживать рукой, чтобы исключить перемещение катушки за счет его магнитного поля.
5. Определить для каждого случая величину индуктивного сопротивления wL. Результаты занести в таблицу 3.
Таблица 3
| Смещение катушки (см) | Iэфф | Uэфф | Р | S | cosj | wL |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите закон Ома для переменного тока.
2. Чему равна средняя мощность в цепи переменного тока?
3. Что такое ваттная, безваттная и полная мощности?
4. Объясните поведение величины cosj в зависимости от вида использованных сопротивлений нагрузки.
5. Как меняется индуктивность катушки в зависимости от глубины насадки железного сердечника?
6. Объясните принцип действия ваттметра.
Лабораторная работа №9
Измерение напряженности магнитного поля соленоида на его оси
Цель работы: Экспериментальное определение величины напряженности магнитного поля на оси соленоидов различной длины и сравнение полученных результатов с теоретическими расчётами.
Приборы и принадлежности: лабораторный стенд, включающий соленоиды и измерительную катушку, звуковой генератор, осциллограф, соединительные проводники.
КРАТКАЯ ТЕОРИЯ
Напряженность магнитного поля на оси кругового тока определяется, как известно, по формуле:
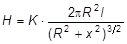 , (1)
, (1)
где К – коэффициент пропорциональности, величина и размерность которой определяется выбором системы измерения единиц (в системе СИ K = 1/4p); R – радиус кругового тока; I – сила тока; x – расстояние от плоскости контура до той точки на оси, где определяется напряженность.
Соленоид состоит из провода, намотанного на цилиндрическую поверхность. Если витки соленоида расположены вплотную друг к другу, то соленоид эквивалентен системе круговых токов одинаковых радиусов, имеющих общую ось. Отсюда напряженность магнитного поля на оси соленоида может быть получена суммированием напряжённостей от отдельных круговых токов.
Найдём напряжённость магнитного поля на оси соленоида в точке A (рис.1). Обозначим плотность витков соленоида n = N/L, где N – полное число витков, L – длина соленоида. На элементарный участок длины соленоида dx приходится dN = n×dx витков. Обозначая силу тока в каждом витке через I, можно участок соленоида рассматривать как круговой ток величиной I×dN.
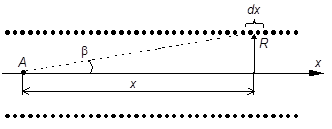 Рис.1. Рис.1. |
Тогда напряженность магнитного поля в точке А на оси соленоида, создаваемая этим участком (dx), в соответствии с (1) будет равна (в системе СИ):
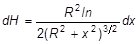 . (2)
. (2)
Вводя в рассмотрение угол b между осью соленоида и радиусом-вектором, проведенным из рассматриваемой точки к участку dx, получим x = RЧctgb. Отсюда
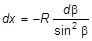 .
.
Кроме того,
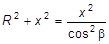 .
.
Подставляя значение |dx| и (R2 + x2) в выражение (2), получим:
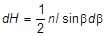 . (3)
. (3)
Так как в точке А вектор напряженности от любого участка направлен вдоль оси соленоида, то для получения результирующего значения Н в точке А следует проинтегрировать выражение (3) по всем значениям b. Если обозначить через b1 и b2 значения углов, соответствующих концам соленоида, то в результате интегрирования получим:
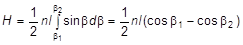 . (4)
. (4)
Для бесконечно длинного соленоида имеем b1 = 0 и b2 = p, откуда
H = n×I.(5)
Направление вектора напряженности магнитного поля на оси определяется согласно правилу правого винта при его вращении по направлению протекания тока по виткам соленоида. Единицей напряженности магнитного поля в системе СИ является А/м (Ампер на метр).
Для всякого конечного соленоида напряженность поля будет меньше, чем для бесконечно длинного. Для соленоида конечной длины наибольшее значение напряженности будет в точке, равноудаленной от концов соленоида. Для точки, находящейся у конца соленоида, напряженность определяется по формуле (4), если в ней положить один угол, например, b2 = p/2, тогда
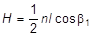 .
.
Если соленоид очень длинный, то b1 » 0, и тогда
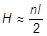 . (6)
. (6)
Из сравнения (6) и (5) видно, что у конца длинного соленоида поле вдвое меньше, чем в середине.
У короткого соленоида даже в его средней части напряженность поля может не достигать величины, определяемой (5), так как углы b1 и b2, под которыми из данной точки видны радиусы концов соленоида, не равны 0 и p. Следовательно, поле в таком соленоиде будет неоднородным по всей длине. Таким образом можно считать, что степень неоднородности поля зависит от относительной длины соленоида l = L/2R, т.е. отношения его длины к диаметру.
На графике (рис.2) дано примерное распределение величины напряженности поля вдоль оси соленоида при различных относительных величинах l.
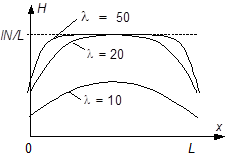 Рис. 2. Рис. 2. |
Из рисунка видно, что, чем больше l, тем более однородным является поле внутри соленоида, и наоборот.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Схема установки, используемой в данной работе, приведена на рис. 3. Для измерения напряженности магнитного поля на оси соленоида L используется катушка Lизм, длина которой много меньше длины исследуемых соленоидов. Это сделано для уменьшения искажений результатов измерений. Измерительная катушка может перемещаться внутри соленоида вдоль его оси.
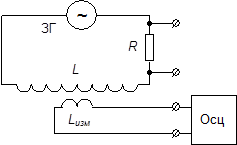 Рис. 3. Рис. 3. |
На соленоид L подаётся переменное напряжение частотой f с генератора ЗГ, в результате чего в соленоиде возникнет переменное магнитное поле, и на катушке Lизм будет наводиться переменная э.д.с., амплитуда которой пропорциональна амплитуде изменения напряженности магнитного поля. Величина э.д.с. на катушке Lизм измеряется с помощью осциллографа.
Для определения амплитуды напряженности магнитного поля воспользуемся следующими простыми соображениями. Э.д.с. индукции, возникающей в измерительной катушке, равна
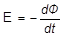 . (7)
. (7)
В свою очередь, магнитный поток
Ф = m0H(t)SNизм,
где H(t) = H0sinwt, w = 2pf, S – площадь сечения одного витка измерительной катушки, Nизм – число витков измерительной катушки.
Пренебрегая магнитным полем самоиндукции измерительной катушки, можно записать величину напряжения UL на выводах Lизм:
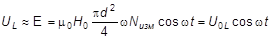 ,
,
где d – диаметр витка измерительной катушки. Таким образом,
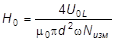 . (8)
. (8)
