Имитационное моделирование детерминированного конечного автомата.

Моделирование нелинейной нестационарной модели средствами SciLab

Цель работы –построение и исследование математической модели нелинейной нестационарной системы.

Постановка задачи

Рассмотрим нелинейную нестационарную систему дифференциальных уравнений (1.1).

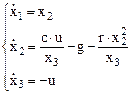;	(1.1)
;

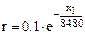Система (1.1) является нестационарной поскольку имеет параметр – 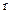, изменяющейся во времени и зависящий от переменной состояния 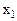. Физической интерпретацией данной системы может являться полет ракетоносителя в атмосфере. В таком случае переменная 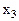описывает массу ЛА изменяющуюся в следствии выгорания топлива, 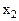– описывает вертикальную составляющую скорости, 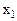– высота полета, а нестационарный параметр 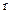– описывает плотность атмосферы зависящую от высоты полета.

Порядок выполнения работы

1. Реализовать в системе SciLab модель нестационарной системы и получить решение при заданных начальных условиях и параметрах, определяемых вариантом (табл.1.).

2. Рассчитать процесс до .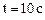

3. Проанализировать зависимость точности и трудоемкости от шага вычислений.

4. Выбрать шаг при заданной точности определения – .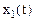

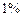Содержание отчета

1. Уравнения описывающие математическую модель нестационарной системы.

2. Начальные условия и параметры системы соответствующие варианту.

3. Решение системы в виде графических зависимостей , , .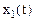

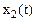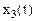4. График зависимости относительной погрешности вычислений от шага вычислений – .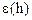

5. Текст программы на языке SciLab.

Условия моделирования

Начальные условия – , .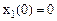

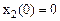Метод численного решения – Кунге-Кутта 4-го порядка.

Шаг вычислений – не более 0.1 с.

.

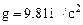Табл.1.

Вариант

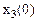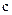Лабораторная работа № 2

Построение имитационной модели нелинейной нестационарной системы средствами Scicos

Цель работы –построение и исследование имитационной нелинейной нестационарной системы.

Рассмотренная в лабораторной работе №1 нелинейная нестационарная система дифференциальных уравнений, может быть преобразована к структурному виду (Рис 1.).

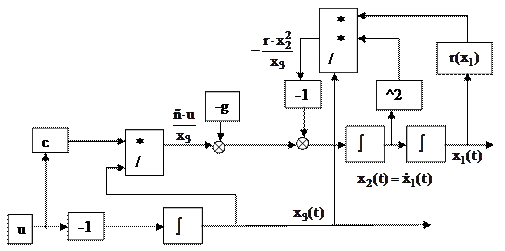Рис.1 – Структурная схема нелинейной нестационарной системы

Порядок выполнения работы

1. Реализовать в системе SciCos модель нестационарной системы и получить решение при заданных начальных условиях и параметрах, определяемых вариантом (табл.2.).

2. Рассчитать процесс до .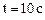

3. Проанализировать зависимость точности и трудоемкости от шага вычислений.

4. Сравнить полученные результаты с результатами лабораторной работы №1.

Содержание отчета

5. Структурная схему нестационарной системы, выполненная в системе SciCos.

6. Начальные условия и параметры системы соответствующие варианту.

7. Решение системы в виде графических зависимостей , , .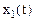

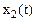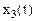8. График зависимости относительной погрешности вычислений от шага вычислений – .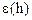

Условия моделирования

Начальные условия – , .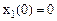

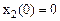Метод численного решения – Кунге-Кутта 4-го порядка.

Шаг вычислений – не более 0.1 с.

.

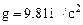Табл.2.

Вариант

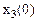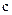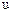Лабораторная работа № 3

Имитационное моделирование детерминированного конечного автомата.

Цель работы –построение исследование модели детерминированного конечного автомата.

Постановка задачи

Теория автоматов получила свое первоначальное развитие в тесной связи с разработкой логических схем цифровой вычислительной техники. Для ее применения при построении моделей систем управления целесообразно уточнить смысл некоторых терминов.

Рассмотрим простейшие и наиболее широко используемые виды конечных автоматов.

1. Автомат Мили (автомат I рода) имеет функции переходов и выходов следующего вида:

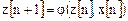;	(3.1)
.

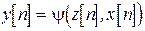где n=0,1,2,... - номер такта. Таким образом, в автомате Мили новое состояние и выходной сигнал выбираются в зависимости от сочетаний текущего состояния и входного сигнала.

2. У автомата Мура (автомата II рода) функции переходов и выходов имеют вид:

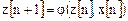;	(3.2)
.

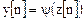Таким образом, здесь новое состояние определяется аналогично автомату Мили, а выходной сигнал зависит только от текущего состояния автомата. Способы задания автомата Мура также рассмотрим на примере.

3. В автономном автомате отсутствуют входные сигналы:

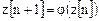;	(3.3)
.

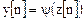Следует отметить, что в любом конечном автономном автомате состояния и выходные сигналы неизбежно начнут периодически повторяться, начиная с некоторого такта. Длина такого периода не превышает количества состояний автомата, а начальное состояние влияет только на номер такта, начиная с которого наступает периодический процесс.

4. Автомат без памяти обеспечивает однозначное отображение входного алфавита X в выходной Y :

;

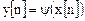(3.4)

5. В автомате без выхода отсутствуют выходные сигналы:

;

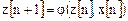(3.5)

Порядок выполнения

1. Построить имитационную модель детерминированного конечного автомата в соответствии с заданным вариантом (табл.3).

2. Разработать тестовый вариант работы автомата.

3. Проверить правильность работы детерминированного конечного автомата в соответствии с тестовым вариантом.

Содержание отчета

1. Модель детерминированного конечного автомата.

2. Тестовый вариант работы автомата, представленный в виде таблицы, матрицы и графа.

3. Результаты работы математической модели автомата.

4. Текст программы на языке SciLab.

Условия моделирования

Табл.3.

Номер варианта	Тип автомата	Количество входов	Количество состояний	Количество Выходов
	Мили
	Мура
	Мили
	Автономный	--
	Без памяти		--
	Мили
	Мура
	Автономный	--
	Мура
	Без памяти		--
	Мили
	Мура
	Мили
	Без выхода			--
	Автономный	--
	Мура
	Мили
	Мили
	Мура

Лабораторная работа № 4