Задачи для решения в аудитории. Дифференциальные уравнения 1-го порядка (3)

Занятие № 3

Дифференциальные уравнения 1-го порядка (3).

Необходимые сведения.

1. Уравнения Бернулли и уравнения Риккати.

• Уравнение Бернулли – это уравнение вида:

Оно сводится к линейному заменой: .

• Метод Бернулли решения линейного уравнения :

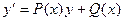ищем решение уравнения в виде .

Тогда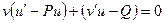

Выберем функцию любую так, чтобы первая скобка =0, т.е. .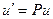

Подставляем её в уравнение и находим .

Перемножая две найденные функции, находим общее решение линейного уравнения.

Таким же методом можно решить и уравнение Бернулли.

• Уравнение Риккати – это уравнение вида:

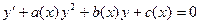
Оно сводится к уравнению Бернулли заменой , где 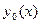- какое-то решение уравнения Риккати

1. Уравнения в полных дифференциалах.

• Уравнение вида 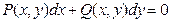, заданное в области D, называется уравнением в полных дифференциалах, если такая непрерывная в D функция 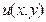, что левая часть уравнения есть полный дифференциал этой функции

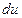( ).Тогда решение .

• Достаточным условием того, что уравнение является уравнением в полных дифференциалах, служит равенство:

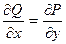
Задачи для решения в аудитории.

1. Т.Р. Задача № 4. Найти общее решение линейного уравнения двумя способами (Методом Лагранжа и методом Бернулли); найти частное решение, удовлетворяющее заданному начальному условию (НУ):

Н.У.: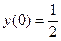

2. Решить уравнение методом Бернулли и сравнить с решением, полученным методом Лагранжа (см.занятие №2) :

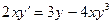
3. Решить уравнения Риккати:

3.1. Указание: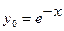

3.2 Указание: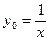

4. Установить, что уравнение является уравнением в полных дифференциалах и найти

его общее решение:

4.1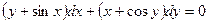

4.2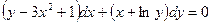

4.3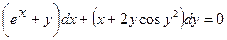

Дифференциальные уравнения 2 курс 3-ий семестр.

5. Т.Р. Задание № 3.Текстовые задачи

5.1 Сила тока в цепи с сопротивлением , индуктивностью и напряжением удовлетворяет уравнению .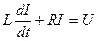

Найти силу тока в момент времени , если

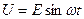а) б) и 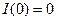( 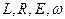- постоянные)

5.2 Количество света, поглощаемого при прохождении через тонкий слой воды, пропорционально количеству падающего на слой света и толщине этого слоя. Зная, что при прохождении слоя воды толщиной 2 м поглощается треть первоначального светового потока, найти какая часть света дойдёт до глубины 12 м.

5.3 Пуля, двигаясь со скоростью , пробивает стену толщиной и вылетает, имея скорость 100 м/c . Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, найти время прохождения пули через стену.

5.4 В помещении вместимостью 10 800 кубических метров воздух содержит 0,12% углекислоты. Вентиляторы доставляют свежий воздух, содержащий 0,04% углекислоты, со скоростью 1500 куб.м/мин. Предполагая, что углекислота распределяется по помещению равномерно в каждый момент времени, найти объёмную долю углекислоты через 10 мин. После начала работы вентиляторов.

5.5 Найти уравнения кривых, у которых длина отрезка нормали постоянна и равна .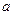

Домашнее задание.

1. Сб.задач Ефимов-Поспелов т.2: №№ 10.86 – 10.95 , 10.96 – 10.105, 10.189, 10.193, 10.195, 10.166, 10.169

Дополнительно: Задачи для подготовки к контрольной работе, защите т.р., экзамену:

1.Сб.задач по ДУ Филиппова: №№ 71-100, 173-176

2.Сб.задач по ДУ Романко: №№ 1-95 (стр.20-23), №№ 1-18 (стр.28-29)