Два подхода к построению моделей

Способов построения моделей существует великое множество, ибо, пытаясь разобраться в сложившемся положении вещей, можно совершенно по-разному упрощать его в надежде вскрыть суть явления, а затем и разрешить.

Правда, не стоит забывать, что нередко упрощенческие подходы к сложным явлениям несут в себе значительную долю опасности.

Можно выделить два подхода к построению моделей (моделированию) тех или иных явлений, событий, обстоятельств, называя один из них западным, а другой восточным.

Западный. В небогатой философами Америке жил в XIX в своеобычный человек по имени Генри Торо (наиболее известная его работа «Уолден или жизнь в лесу» переведена на русский язык). Ему принадлежат слова: «Мы часто принимаем полутораумных людей как полоумных, потому что нам доступна лишь треть их ума».

Весьма нетривиальное высказывание, декларирующее по сути бесконечное уважение ко всякому человеку. А вот – математическая формула, навеянная этим высказыванием и в известном смысле точно его передающая: .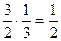

Выписанное равенство определяется сформулированной сентенцией, оно абсолютно правильно, но способно заменить это высказывание в очень малой степени – формула отражает лишь количественную сторону высказывания, но почти абстрагируется от его смысла.

Восточный. Однажды шах, отличавшийся крутым нравом, пожелал иметь свой парадный портрет. Это пожелание шаха само по себе ничего страшного не таило, однако художник, которому была оказана столь высокая честь, впал в отчаяние. И было отчего: шах был кривым на один глаз.

Конечно, можно было бы написать портрет шаха с двумя глазами. Но такой портрет вряд ли понравился бы заказчику – слишком явной была бы неправда. Можно было бы изобразить шаха, как есть – одноглазым. Но это вызвало бы шахский гнев (в этом чувства шаха вполне понятны и нам – неудачная фотография если и сохраняется, то на почетном месте обычно не вывешивается).

Казнь, как неизбежное следствие шахского гнева, казалась неминуемой. Однако жизнелюбивый художник после мучительных размышлений выход все же нашел.

Шах был изображен на охоте – восседая на великолепном коне, он целился из лука в не менее великолепного оленя. Один глаз был зажмурен.

Нужно ли объяснять, какой именно?

Во всех случаях портрет передает лишь часть того, что можно было бы рассказать о человеке. Отбор этой части определяется целью. У художника их было две – написать парадный портрет шаха и остаться живым.

Три типа моделей

Различают три типа моделей – физические, аналоговые и математические модели.

Физические модели. Так называют увеличенное или уменьшенное описание объекта или системы. Отличительная характеристика физической модели состоит в том, что в некотором смысле она выглядит как моделируемая целостность. Примером физической модели может служить игрушечная машинка, кукла, всем известны из астрономии модель солнечной системы, а из химии – модель атома или молекулы и т.п.

Применяются физические модели в машиностроении, самолетостроении, архитектуре и т.д.

Например, на одном из этапов разработки самолета новой конструкции возникает необходимость проверить его основные аэродинамические параметры. С этой целью подготовленную копию (модель) продувают в специальной (аэродинамической) трубе, а полученные показания затем тщательно исследуют. Выгода такого подхода очевидна. И потому все ведущие самолетостроительные компании используют физические модели подобного рода при разработке каждого нового летательного аппарата.

Аналоговые модели. Так называют модели, представляющие исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой.

Примерами аналоговых моделей являются графики, таблицы, диаграммы, карты (местности).

Например, нужно найти наиболее экономичный способ для регулярных известных поставок товаров в три города, построив для этого только один склад. Основное требование: место для склада должно быть таким, чтобы полные транспортные расходы были наименьшими (считается, что стоимость каждой перевозки равна произведению расстояния от склада до пункта назначения на общий вес перевозимых товаров и измеряется в тонно-километрах).

Наклеим карту местности на лист фанеры. Затем в месте нахождения каждого города просверлим сквозные отверстия, пропустим через них нити и привяжем к ним грузики, пропорциональные запросам товаров в этот город. Свяжем свободные концы нитей в один узел и отпустим. Под действием силы тяжести система придет в состояние равновесия. То место, которое при этом займет узел, и будет соответствовать оптимальному расположению склада.

Математические модели. Так называют модели, использующие для описания свойств и/или характеристик объекта или события математические символы и методы.

Если некоторую проблему удается перенести на язык формул, то она сильно упрощается. Математический подход прост еще и потому, что он подчиняется вполне определенным жестким правилам, которые нельзя отменить указом или иным способом.

Сложность нашей жизни как раз и состоит в том, что многое, что в ней случается, нередко свободно от пут каких бы то ни было условностей.

Математика имеет дело с упрощенным описанием явлений. По-существу, любая формула (или совокупность формул) представляет собой определенный этап в построении математической модели.

Опыт показывает, что построить модель (написать уравнение, неравенство или систему уравнений или неравенств) довольно легко. Трудно в этой модельной и, следовательно, упрощенной форме суметь передать суть изучаемого явления.

«Для нахождения приемлемого или оптимального решения задачи полезно знать, в чем она состоит. Как ни просто и прозрачно данное утверждение, чересчур многие … игнорируют очевидное» ( Р. Шеннон).

7.3 Что такое математическое моделирование?

С середины ХХ в. В самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как «математическая экономика», «математическая химия», «математическая лингвистика» и т.д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Математическая модель – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования – исследовать эти объекты и предсказать результаты будущих наблюдений. Однако, моделирование – это еще и метод познания окружающего мира, дающий возможность управлять им.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории. Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

В рассказе знаменитого польского фантаста С. Лема «Путешествие второе или какую услугу оказали Трурль и Клапауций царю Жестокусу» из цикла «Кибериада» так описывается процесс математического моделирования ситуации:

«И друзья засели за эксперимент. Он состоял в том, что конструкторы смоделировали царя Жестокуса и чудовище, но лишь на бумаге, математическим методом; Трурль управлял первой моделью, а Клапауций – второй. Вот и сшиблись модели-враги на огромных белых листах, покрывающих стол, с такой силой, что лопнули графитовые стержни в карандашах. Неопределенным интегралом яростно извивался монстр под ударами царевых уравнений и повергался, рассыпанный в несчетное множество неизвестных, и восставал вновь, возведенный в высшую степень, а царь поражал его дифференциалами, да так, что лишь клочья функциональных операторов летели в разные стороны, и возник в результате такой нелинейно-алгебраический хаос, что конструкторы не могли уж разобраться, что стало с царем, а что – с чудовищем, и тот и другое исчезли во мгле перечеркнутых знаков. Встали друзья из-за стола и для подкрепления сил хлебнули из огромной лейденской амфоры, вновь уселись и снова начали бой, стремительный бой, спустив с цепи весь Высший Анализ; прах заклубился на бумаге, и чад пошел от раскаленных графитов. Мчался царь во весь опор свирепых своих коэффициентов, блуждал по лесу символов шестииндексных, возвращался по собственному следу, атаковал монстра до седьмого пота и восьмой равнодействующей, а чудовище распалось на сто многочленов, потеряв один икс и два ипсилона, забралось в знаменатель, вылупилось из кокона, взмахнуло корнями и как ударит математизированную царскую особу по боку, так что содрогнулось все царево уравнение, словно ударом наотмашь пораженное. Но тут Жестокус броней нелинейной прикрылся, бесконечно удаленной точки достиг, мигом вернулся и как ударит чудовище по голове сквозь все скобки, так что логарифм отвалился у монстра спереди, а степень – сзади. Втянуло чудовище щупальца внутрь и ковариантно – лишь карандашики мелькали – бац! Бац! – нанесло удар за ударом и еще один – по спине трансформаторной – и вот уже царь, упрощенный, зашатался от числителя и до всех знаменателей, и вытянулся во весь рост, а конструкторы, вскочив из-за стола, стали смеяться и рвать в клочья исписанные листы на глазах у соглядатаев, которые тщетно пытались подсматривать за ними…, но с высшей математикой незнакомые, поняли лишь, что конструкторы кричат один другому: “Победа! Победа!”»