Раздел 3. Аналитическая геометрия на плоскости.

Лекция 3.1. Прямая на плоскости.

Краткое содержание: Различные виды уравнений прямой на плоскости. Взаимное расположение двух прямых. Угол между прямыми на плоскости. Расстояние от точки до прямой.

Из школьного курса геометрии нам хорошо известно, что такое прямая. Попробуем определить прямую на языке векторов. Зафиксируем некоторую точку 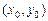на плоскости и зададим вектор 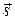(так называемый направляющий вектор). Если откладывать от точки 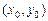всевозможные векторы, коллинеарные данному вектору 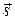, то концы этих векторов составят множество точек, которое и является прямой. Построенная прямая проходит через точку 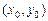в направлении 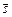.Обозначим через 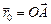радиус-вектор точки 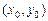, а через 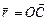- радиус-вектор произвольной точки (х, у) на прямой (рис. 1). Тогда по построению вектор 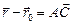коллинеарен направляющему вектору 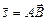. Это значит, что найдется действительное число 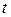, такое, что 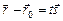или . 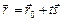Перебирая все возможные значения параметра 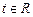, мы получим радиусы-векторы всех точек данной прямой. Итак, построено векторное уравнение прямой .

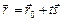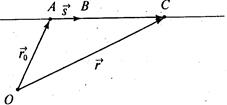Рис. 1

Если 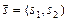, легко записать параметрические уравнения прямой:

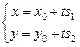, где .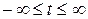

Исключим параметр 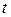. Для этого можно, например, первое равенство умножить на 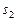, а второе - на 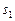: 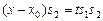и 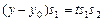. Тогда 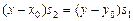откуда, раскрыв скобки, получим 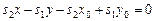Обозначим 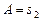, , 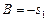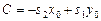. Тогда получается общее уравнение прямой .

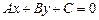Мы проверили, что координаты точки, которая лежит на прямой, проходящей через точку 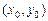в направлении вектора 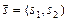, удовлетворяют этому уравнению. Нетрудно проверить и обратное утверждение. Итак, данное уравнение действительно является общим уравнением прямой. Прямая, заданная своим общим уравнением, имеет направляющий вектор 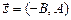, в общее уравнение входят только первые степени х и у (в отличие, скажем, от уравнения окружности). Поэтому прямая на плоскости есть линия первого порядка.

Пусть задан вектор 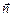, перпендикулярный направляющему вектору s (рис. 2). Вектор 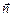- это так называемая нормаль. Тогда 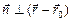и по свойству скалярного произведения справедливо равенство 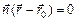, которое называется нормальным уравнением прямой.

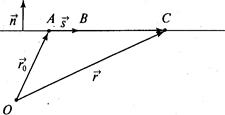Рис. 2

Поскольку точка 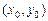лежит на прямой, ее координаты удовлетворяют общему уравнению 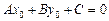. Вычитая это равенство из общего уравнения, получаем равенство 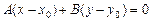, которое совпадает с нормальным уравнением при 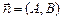. Итак, .если задано общее уравнение прямой, то нормаль к ней имеет коор-|динаты 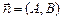. При этом очевидно, что 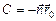. Пусть задано общее уравнение прямой и 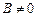. Тогда уравнение можно разделить на В и, обозначив 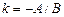, , 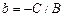получить хорошо знакомое «школьное» уравнение прямой .

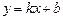Другими словами, при 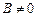прямая представляет собой график линейной функции. Коэффициент k равен тангенсу угла наклона прямой к оси х и называется угловым коэффициентом прямой. Число b — это ордината точки пересечения прямой с осью у: говорят, что прямая отсекает отрезок b на оси у (рис. 3).

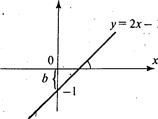Рис. 3

Предположим теперь, что все коэффициенты общего уравнения не равны нулю. Если разделить общее уравнение на С, получится равенство 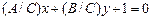, которое можно записать в виде 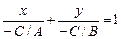, или, обозначив 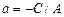, , 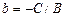в виде: 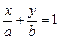. Такое уравнение называется «уравнением прямой в отрезках». В самом деле, .при 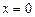имеем 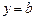, а при 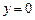соответственно 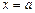. Таким образом, числа а и b есть отрезки, отсекаемые прямой на осях координат (рис. 4).

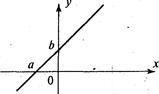Рис. 4

В итоге получено шесть различных уравнении прямой:

Векторное: .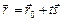

Параметрические: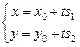

Общее: ,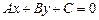

Нормальное: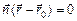

Уравнение прямой с угловым коэффициентом: .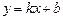

В отрезках .

Пр: Рассмотрим прямую, заданную общим уравнением 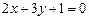с коэффициентами 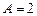, , 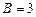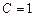(рис. 5). Ее направляющий вектор 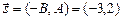, вектор нормали 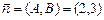. В качестве начального вектора 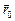можно взять радиус-вектор любой точки, лежащей на прямой, например 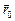= 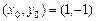. В самом деле, 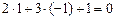, значит, данная точка принадлежит прямой. Проверим, например, что : .

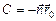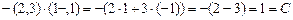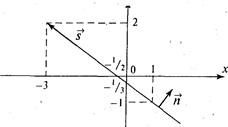Рис. 5

Убедимся, что тот же результат получится, если в качестве 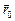взять любую другую точку на прямой. Для этого выразим у через х, т.е. выпишем уравнение прямой с угловым коэффициентом уравнение прямой 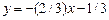Из него, кстати, видно, что прямая наклонена к оси х под тупым углом 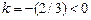и пересекает ось ординат в точке 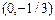. Пусть произвольная точка прямой имеет абсциссу 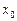. Тогда ее ордината равна 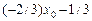. Посчитаем в этом случае величину :

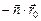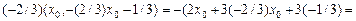
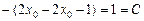
Таким образом, неважно, какую именно точкувзять за начальную.

Найденные векторы 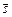и 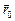дают следующие параметрические уравнения прямой:

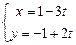. Выведем еще уравнение в отрезках. Для этого коэффициенты общего уравнения разделим на 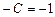: 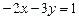или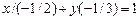

Из уравнения видно, что прямая пересекает ось абсцисс в точке 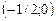. Точку пересечения ординат 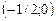мы уже нашли.