Совершенные нормальные формы

Определение 5. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ее ДНФ, обладающая следующими свойствами:

1. Она не содержит двух одинаковых слагаемых.

2. Ни одно слагаемое не содержит одновременно двух одинаковых сомножителей.

3. Ни одно слагаемое не содержит одновременно некоторого высказывания и его отрицания.

4. Каждое слагаемое содержит в качестве сомножителя либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.

Это определение является конструктивным, т.е. позволяет для каждой формулы алгебры высказываний, приведенной к ДНФ, построить ее СДНФ.

Упражнение

.

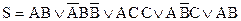Задана ДНФ. Приведем ее к СДНФ.

1. Первое и последние слагаемые одинаковы. На основании свойства операции дизъюнкции АÚА=А одно из одинаковых слагаемых можно отбросить.

2. АСС=АС.

3. .

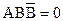Получим .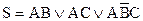

Теперь выполнили условия 1 - 3. Чтобы выполнить условие 4, поступим следующим образом:

;

.

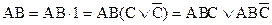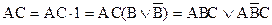Следовательно, .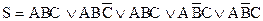

Теперь условие 4 выполнено, но появились одинаковые слагаемые. Исключив их получим:

.

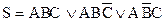Определение 6. Совершенной конъюнктивной нормальной формой данной формулы алгебры высказываний (СКНФ) называется такая ее КНФ, которая удовлетворяет следующим свойствам:

1. Она не содержит двух одинаковых сомножителей.

2. Ни один из сомножителей не содержит одновременно двух одинаковых слагаемых.

3. Ни один из сомножителей не содержит одновременно некоторого высказывания и его отрицания.

4. Каждый сомножитель СКНФ содержит в качестве слагаемого либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.

Определение СКНФ также является конструктивным.

Упражнение

Дана КНФ: .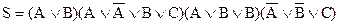

Построить СКНФ.

Совершенные нормальные формы могут быть применены для установления равносильности двух заданных формул алгебры высказываний. Для этого нужно обе формулы привести к СКНФ или СДНФ и убедить в их совпадении. Например, формулы

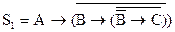и 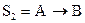равносильны:

.

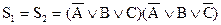Полной элементарной конъюнкцией называется конъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 5. Аналогично, полной элементарной суммой называется элементарная дизъюнкция, удовлетворяющая свойствам 2, 3,4 определения 6.

Поэтому совершенные нормальные формы можно определить так:

Определение 7. Совершенной дизъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией различных полных элементарных конъюнкций.

Определение 8. Совершенной конъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией различных полных элементарных дизъюнкций.

Каждая полная элементарная конъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 1: переменное высказывание, входящее без знака отрицания, принимает значение 1, а со знаком отрицания - 0. Этот набор значений элементарных составляющих называется единицей данной полной элементарной конъюнкции. Так единицей полной элементарной конъюнкции 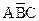является (1, 0,1).

Аналогично. Каждая полная элементарная дизъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 0: переменное высказывание, входящее без знака отрицания, принимает значение 0, а со знаком отрицания - 1. Этот набор значений элементарных составляющих называется нулем данной полной элементарной дизъюнкции. Так нулем полной элементарной дизъюнкции 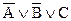является (1, 1,0).