Формула определения бета - коэффициента

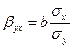
Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину среднего квадратического отклонения.

Пример

По представленным данным о спросе и доходе населения за ряд текущих лет построить уравнение регрессии.

Год	Доход, Х	Спрос, Y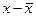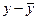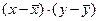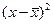
			-5	-3,3	16,5
			-3	-1,3	3,9
			-1	-1,3	1,3
		10,3
		10,5		1,2	3,6
				3,7	18,5
Итого		55,8			44,80	70,00
Среднее		9,3			7,47	11,67

Уравнение парной регрессии имеет вид:

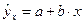
Параметры модели определим по формулам:

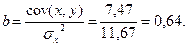
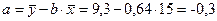
Коэффициент b показывает, что с увеличением дохода на 1 у.е., спрос возрастёт на 0,64 у.е.

Уравнение парной регрессии примет вид:

.

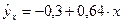Построим на диаграмме зависимость Y от Х и добавим линию тренда, используя линейную модель для описания данных:

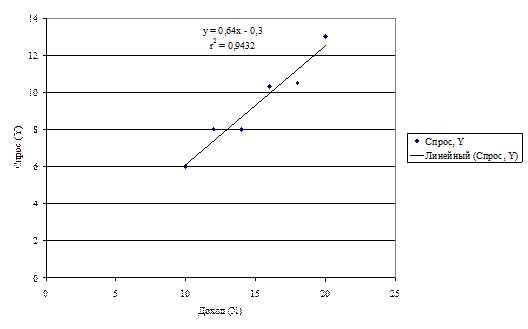
Проверка модели на адекватность

Понятие адекватности, в какой-то мере, условно, так как полного соответствия модели реальному объекту быть не может, иначе это был уже сам объект. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые для исследования считаются существенными.

Проверка значимости коэффициентов регрессии по t-критерию Стьюдента

Выдвигается гипотеза о случайной природе показателей a и b, т.е. о незначимом их отличии от нуля. Сопоставляем величину случайной ошибки со значением t-критерия:

; ,

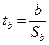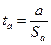где 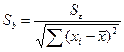; 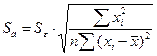, где .

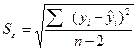Если 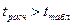, то гипотеза отклоняется, т.е. a и b не случайно отличаются от нуля и сформировались под влиянием фактора х.

Определение доверительных интервалов

Рассчитываем предельную ошибку каждого показателя:

,

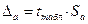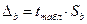
и доверительные интервалы для значений параметров линейной регресси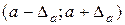и:

и .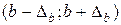

Проверка значимости уравнения регрессии по F-критерию Фишера

Для проверки значимости уравнения регрессии в целом, используют F- критерий Фишера. В случае парной регрессии значимость модели определяется по формуле:

.

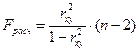Если F_расч > F_табл, то модель считается значимой. Гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надёжность.

Проверка модели на наличия или отсутствия систематической ошибки

Установление наличия или отсутствия систематической ошибки на основе ряда остатков (отклонений расчетных значений результативного признака от фактических значений) 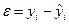происходит на основании пяти требований:

1. Уровни ряда остатков должны иметь случайный характер;

2. M[ε] = 0.

3. D[ε] = const, свойство гомоскедастичности;

4. Значения уровней ряда остатков независимы друг от друга (отсутствует автокорреляция);

5. Уровни ряда остатков распределены по нормальному закону.