Застосування схеми Горнера.

1. Розкладання полінома за степенями бінома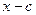

Задача

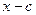Розкласти поліном за степенями біному , тобто подати поліном у вигляді

Розв’язання.

Звернемо увагу, що в комірках другого стовпчика з першої до передостанньої стоять коефіцієнти неповної частки . Це поліном із степенем на 1 меншим, ніж у вихідного полінома. Його теж можна розділити на 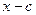, використовуючи схему Горнера. Процес ділення на 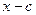можна подати так:

, (5)

- неповна частка, - остача від ділення на 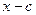. Коефіцієнти для беруть із відповідної схеми Горнера.

Підставимо (5) у (3):

.

Процес розкладання проводиться до полінома . Розкладання кожного разу підставляється до 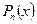. На кінцевому етапі будемо мати розкладання

(6),

Тобто коефіцієнти розкладання будуть такі:

Приклад 2

Розкласти за степенями бінома поліном .

Розв’язання.

Складемо схему Горнера ділення на біном :

		-2		-5
2i		-2+2i	-3-4i	3-6i	19+6i

Отже, .

Застосуємо схему Горнера для .

		-2+2i	-3-4i	3-6i
2i		-2+4i	-11-8i	19-28i

Отже, .

Підставимо розкладання до :

Застосуємо схему Горнера для :

		-2+4i	-11-8i
2i		-2+6i	-23-12i

Підставимо розкладання до :

Застосуємо схему Горнера для :

		-2+6i
2i		-2+8i

Підставимо розкладання до :

Отримали розкладання поліном за степенями бінома :

Коефіцієнти розкладання:

Процес розкладання можна позбавити громіздких викладок, якщо помітити, що коефіцієнтами розкладання є залишки у кожному розкладанні поліномів за схемою Горнеоа.

Для наочності процесу доцільно усі схеми об’єднати в одну.

Об’єднана схема Горнера.

		-2		-5
2i		-2+2i	-3-4i	3-6i	19+6i
2i		-2+4i	-11-8i	19-28i
2i		-2+6i	-23-12i
2i		-2+8i
2i

З останньої схеми видно, що коефіцієнти розкладання полінома за степенями розташовані в останніх комірках кожного рядка, і є коефіцієнтами біля степенів розташованих в порядку зростання з гори до низу.

Обчислення похідних полінома в даній точці .

Задача.

Обчислити значення похідних полінома до n-ї включно в точці .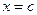

Розв’язання.

З попередньої задачі маємо розкладання полінома 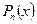за степенями бінома 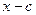(6):

.

Для отримання значень похідних полінома до n-ї включно в точці 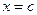запишемо розкладання функції в ряд Тейлора в околі точки 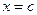і порівняємо два розкладання.

Ряд Тейлора для будь якої безкінечно диференційованої функції в околі точки 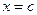має такий вигляд:

- значення функції та її похідних у точці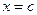

В нашому випадку 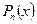є функція, диференційована n раз, отже для неї ряд Тейлора прийме вигляд:

, (7)

Де - значення полінома та його похідних у точці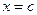

Порівняємо (6) і (7).

З порівняння можна записати таке:

Приклад 3

Обчислити значення похідних полінома з попереднього прикладу до 4-ї включно в точці .

Розв’язання.

Розглянемо об’єднану схему Горнера з попереднього прикладу. В останній комірці кожного рядка маємо значення .