Примеры применения теоремы Гаусса
1. Электростатическое поле бесконечной равномерно заряжен-ной плоскости.
Бесконечная плоскость заряжена с постоянной поверхностной
плотностью + (рис. 1.6.1). Из соображений симметрии следует, что
вектор E направлен перпендикулярно плоскости. Так как заряженная плоскость бесконечная, то числовое значение напряженности Е ее по-ля будет одинаковым во всех точках пространства, расположенных на одинаковых расстояниях слева и справа от плоскости. В качестве замкнутой поверхности выберем цилиндрическую поверхность, осно-вания которой параллельны плоскости, а ось перпендикулярна ей. То-гда в точках левого и правого оснований проекция En = E = const, а в
точках боковой поверхности Еn = 0, т. к. вектор E перпендикулярен
нормали n к боковой поверхности. Поток вектора E через замкнутую цилиндрическую поверхность будет равен:
| En dSEn dSE n dS | En dSEn dSEn dS | ||||
| S | S1 | S 2 | S бок | S1 | S2 |
| EdS EdS 2 E dS 2 ES. | (1.6.1) | ||||
| S | S | S |
Заряд, заключенный внутри построенной цилиндрической по-верхности, равен: q = S. Согласно теореме Гаусса получаем:
| E n dS | q | 2ES | S | E | . | (1.6.2) | |||||||||||||||
| 0 | 0 | ||||||||||||||||||||
| S | 2 0 | ||||||||||||||||||||
| + > 0 | E | ||||||||||||||||||||
| E | |||||||||||||||||||||
| l | l | dS | |||||||||||||||||||
| n | |||||||||||||||||||||
| n | dS | + + | S | E | n | ||||||||||||||||
| + + + + | |||||||||||||||||||||
| + + + + | q = S | ||||||||||||||||||||
| E | + + | E | |||||||||||||||||||
| S2 | S1 | ||||||||||||||||||||
| E | |||||||||||||||||||||
| E |
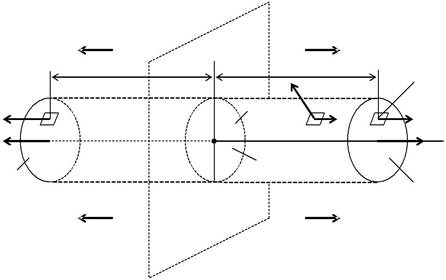
Рис. 1.6.1
Напряженность электростатического поля бесконечной равно-мерно заряженной плоскости определяется выражением
| E | . | (1.6.3) | ||
| 2 0 | ||||
Из формулы (1.6.3) следует, что напряженность не зависит от рас-стояния до плоскости, а следовательно, она одинакова по модулю во всех точках поля. Это означает, что поле равномерно заряженной плоскости однородно.
2. Электростатическое поле бесконечной равномерно заряжен-ной нити.
Найдем поле бесконечной равномерно заряженной нити с ли-нейной плотностью заряда (рис. 1.6.2). Из соображений симмет-рии следует, что вектор напряженности E электрического поля на-
правлен радиально, т. е. перпендикулярно к оси заряженной нити. Причем во всех точках, равноудаленных от оси нити, численные значения напряженности Е поля одинаковы. Поэтому в качестве замкнутой выберем цилиндрическую поверхность, основания кото-рой перпендикулярны нити, а ось совпадет с ней. Тогда во всех точ-ках верхнего и нижнего оснований проекция вектора напряженно-сти на нормаль Еn = 0, а в точках на боковой поверхности En = E =
= const, т. к. вектор E совпадает с нормалью n к боковой поверхно-
сти. Поток вектора E через замкнутую цилиндрическую поверх-ность будет равен:
| En dSEn dS | En dSEndS | |||||
| S | S1 | S бок | S2 | |||
| En dS E dS ESбок E 2 rl. | (1.6.4) | |||||
| S бок | Sбок | |||||
| n | > 0 | |||||
| S | ||||||
| r | ||||||
| l | dS | |||||
| n |
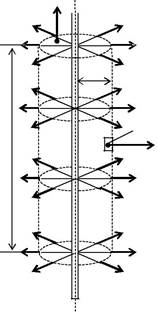
n 
Рис. 1.6.2
Заряд, заключенный внутри построенной цилиндрической по-верхности, равен: q = l. Согласно теореме Гаусса получаем:
| EndS | q | E 2 rl | lE | . | (1.6.5) | ||||
| 0 | 0 | 2 0r | |||||||
| S |
То есть получаем, что напряженность электрического поля, созда-ваемого бесконечной равномерно заряженной нитью, равна:
| E | . | (1.6.6) | ||
| 2 0r | ||||
3. Электростатическое поле равномерно заряженной сферы.
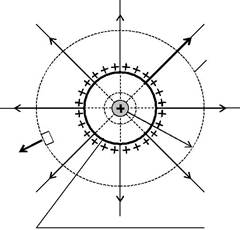
Сферическая поверхность радиуса R с общим зарядом q заря-жена равномерно с поверхностной плотностью + . Благодаря рав-номерному распределению заряда по поверхности поле, создавае-мое им, обладает сферической симметрией. Линии напряженности будут направлены радиально. Поэтому выберем замкнутую по-верхность в виде сферы S радиуса r, имеющей общий центр с заря-
женной сферой. В этом случае вектор E , направленный по радиаль-ным линиям, в любой точке выбранной сферической поверхности будет перпендикулярным поверхности и одинаковым по модулю:
En = E = const (рис. 1.6.3).
| E | ||
| S1 | ||
| Sсф | q > 0 | |
| S2 | ||
| dS | r | |
| n | ||
Сфера радиуса R
Рис. 1.6.3
1) рассмотрим поле вне сферы (r > R). Внутрь выбранной поверх-ности S1 попадает весь заряд q сферы:
| q Sсф4 R2 . | (1.6.7) | ||||||||||
| Применим теорему Гаусса: | |||||||||||
| E dS | q | E 4 r2 | q | E | q | . | (1.6.8) | ||||
| 0 | 0 | ||||||||||
| S | 4 0 r | ||||||||||
С учетом формулы (2.16) получаем:
| E | R2 | ; | (1.6.9) | |
| 0r2 | ||||
2) рассмотрим поле внутри сферы (r < R). Замкнутая сферическая поверхность S2 не содержит внутри зарядов, поэтому
| E n dS 0 | EdS 0 | E dS 0E 0. (1.6.10) |
| S 2 | S 2 | S2 |
То есть внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).
E
 E 1
E 1 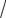 r2
r2
0 E = 0
R r
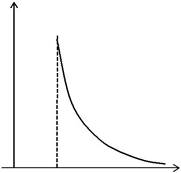
Рис. 1.6.4
Графическая зависимость напряженности Е электростатического поля равномерно заряженной сферы от расстояния r представлена на рис. 1.6.4.
