Методы одномерной оптимизации.

Практика 1

1. Метод сканирования.

Метод сканирования заключается в последовательном переборе всех значений a≤x≤b с шагом ε (погрешность решения) с вычислением критерия оптимальности R в каждой точке. Путем выбора наибольшего из всех вычисленных значений R и находится решение задачи x*.

Достоинство метода сканирования состоит в том, что можно найти глобальный максимум критерия, если R(x) – многоэкстремальная функция.

К недостаткам данного метода относится значительное число повторных вычислений R(x), что в случае сложной функции R(x) требует существенных затрат времени.

На практике можно реализовать одну из основных модификаций метода:

1) последовательное уточнение решения (сканирование с постоянным шагом);

2) сканирование с переменным шагом.

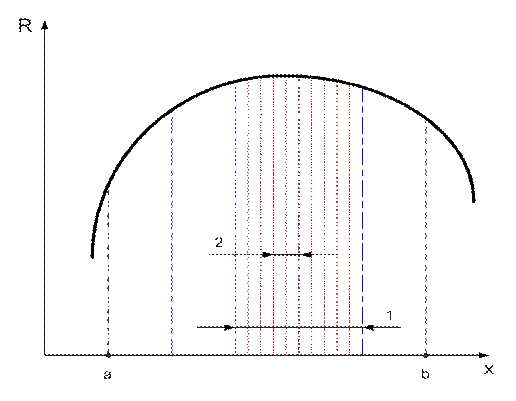
Рис. Модифицированный метод сканирования:

1 – интервал, включающий в себя искомый максимум функции после первого этапа сканирования (исходный участок разбит на 5 участков );

2 – то же, после второго этапа.

На первом этапе сканирование осуществляется с крупным шагом, затем отрезок, внутри которого получено наибольшее значение R(x), разбивается на более мелкие отрезки, ищется новый отрезок, внутри которого находится уточнённое значение максимума.

Новый отрезок опять делится на более мелкие отрезки и так далее до тех пор, пока величина отрезка, содержащего максимальное значение R(x), не будет меньше заданной погрешности. Главный недостаток этого варианта метода – возможность пропуска строгого глобального максимума.

1. Метод деления отрезка пополам.

Метод основан на делении текущего отрезка [a,b], где содержится искомый экстремум, на две равные части; с последующим выбором в качестве следующего текущего отрезка одной из половин, в которой локализуется максимум,. Экстремум локализуется путём сравнения двух значений критерия оптимальности в точках, отстоящих от середины отрезка на Е/2, где Е – погрешность решения задачи оптимизации.

Если R (х+Е/2)>R(x-Е/2), то максимум располагается на правой половине текущего отрезка [a,b], в противном случае – на левой. Процесс поиска завершается при достижении отрезка [a,b] величины заданной погрешности Е. К недостаткам метода относится его работоспособность только для одноэкстремальных функций R(x). (Функция R(x) называется одноэкстремальной, если содержит один экстремум того типа, который мы ищем в задаче). В других случаях, при сравнении двух критериев оптимальности в соседних точках, невозможно правильно выбрать следующий интервал, где находится максимум.

Существует и другой вариант алгоритма, заключающийся в следующем. После нахождения середины отрезка в одной из половин, находят среднюю точку и, сравнивая значения функций в этих точках, распределяют, в какой из половинок находиться экстремум. Если R(C₁)<R(C₂), то в качестве следующего отрезка выбираем отрезок [a,c₁], если R(C₁)>R(C₂), то берут новую точку в середине правой половины и в ней вычисляют функцию. В зависимости от сравнения значений функций в точках С₃ и С₁ и выбирают новый отрезок [с₁,b] или [c₂, c₃] и т.д.

Второй вариант метода не имеет с точки зрения эффективности принципиального отличия от первого, так как эффективность принято оценивать по наихудшему варианту.

Малое отклонение от текущей точки обеспечивают в процессе поиска отсутствие шатаний, сопровождающихся резкими отклонениями состояния системы.

Пример: Дана функция R(x)=DSin(Ax+C), где коэффициенты имеют следующие значения: А=1,0; В=1,0; С=1,0; D=1,0. Найти максимум функции на следующем интервале: [-1;2]. Ошибка задается по х: Е=0,05

Результаты расчетов:

Середина отрезка х₀ = 0,5

Значения критерия R₀=0.9975

Значение R(0.5-Е/2)=R(0.475)=0.97922273

Значение R(0.5+Е/2)=R(0.525)=0.9989513

Следовательно, искомый максимум лежит в правой половине отрезка, то есть теперь отрезком является [0.5;2].

Далее приведем координаты середины отрезков с номером итерации, значение критерия в них и указывается новый отрезок (правый или левый).

№ итерации	х	R/x	отрезок
	X1=1.25	R1=0.77807320	Левый
	X2=0.875	R2=0.95408578	Левый
	X3=0.6875	R3=0.993193785	Левый
	X4=0.59375	R4=0.99973658	Левый
	X5=0.546875	R5=0.997139

(х₄-х₅)<E, поэтому решение находиться в области найденных значений или середину между ними. Всего 8 раз (4*2=8) вычислялся критерий оптимальности.

1. Метод золотого сечения.

Метод основан на делении отрезка [a,b], где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для определения следующего отрезка, содержащего максимум. Золотое сечение определяется по правилу: отношение всего отрезка к большей его части равно отношению большей части отрезка к меньшей.

Ему удовлетворяют две точки с, d, расположенные симметрично относительно середины отрезка. Термин «Золотое сечение» ввел Леонардо да Винчи, его применяли при композиционном построении многих произведений мирового искусства, в том числе в античной архитектуре и в эпоху Возрождения.

Рассмотрим k–й шаг последовательного поиска.

Выбираем на отрезке [a,b] две точки с, d, причём такие, которые удовлетворяют равенству: ab – ad = ac = db. При этом с<d, и эти точки выбраны симметрично относительно середины отрезка [a,b].

В этом случае выполняется следующее соотношение:

.

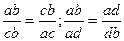При этом, отношение длин отрезков сохраняется от шага к шагу, т.е.:

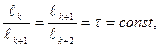(1.1)

где 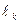, , 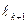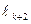- длины отрезков соответственно на k-ом, (k +1)-ом и (k +2)-ом шаге соответственно.

Число 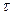называется отношением золотого сечения. Выясним, чему оно равно.

Предположим, что на k-ом шаге выбран отрезок [a,d]. Тогда на (k +1)-ом шаге одной из точек деления, а именно правой будет точка c. Значит длина отрезка 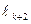, выбираемого на (k +1)-ом шаге, совпадает с длиной отрезка [a,c] и верно следующее равенство:

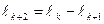. (1.2)

Подставим выражение (1.2) в (1.1), получим:

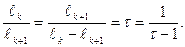. (1.3)

Преобразуем это соотношение, придём к квадратному уравнению:

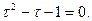
Это уравнение имеет единственное положительное решение: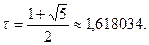

Точки c и d определяем следующим образом:

.

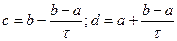Путем сравнения R(c) и R(d), определяют следующий отрезок, где содержится максимум.

Если R(c)<R(d), то в качестве следующего отрезка выбираем отрезок [a,d]. В противном случае выбираем [с,b].

Новый отрезок снова делим на неравные части по правилу золотого сечения:

.

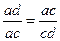Следует отметить, что точка d является и точкой золотого сечения отрезка [c,b]:

т.е. .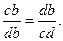

Поэтому, на каждой следующей итерации нужно вычислять только одно значение критерия оптимальности.

Условие окончания поиска: величина отрезка, содержащего максимальное значение R(x), должно быть меньше заданной погрешности ε.