Булева алгебра. алгебра логики

Зная определения логических операций отрицания, конъюнкции и дизъюнкции, легко убедиться в следующих их свойствах.

1. Коммутативность дизъюнкции и конъюнкции:

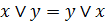, (6.1д)

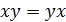. (6.1к)

2. Ассоциативность дизъюнкции и конъюнкции:

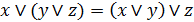; (6.2д)

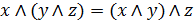. (6.2к)

3. Дистрибутивность дизъюнкции относительно конъюнкции и конъюнкции относительно дизъюнкции:

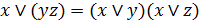; (6.3д)

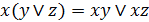. (6.3к)

4. Законы действий с константами:

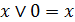; (6.4д)

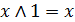; (6.4к)

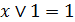; (6.5д)

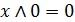. (6.5к)

5. Законы действий с отрицанием:

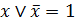;. (6.6д)

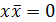. (6.6к)

Из этих свойств можно получить все остальные свойства операций тождественными преобразованиями логических формул.

6. Законы де Моргана:

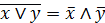; (6.7д)

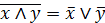. (6.7к)

7. Законы поглощения:

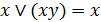; (6.8д)

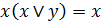. (6.8к)

8. Законы идемпотентности:

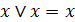; (6.9д)

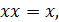(6.9к)

которые дают возможность записывать логические формулы без коэффициентов и показателей степени.

Множество 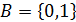, на котором определены операции отрицания, дизъюнкции и конъюнкции со свойствами (6.1 ― 6.6), называется булевой двухэлементной алгеброй.

Алгеброй логики называется двухэлементная булева алгебра, дополненная операциями импликации ( 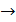) и эквивалентности (~).

Для преобразования формул в формулы булевой двухэлементной алгебры (в дальнейшем, просто булевой алгебры) необходимо использовать равенства:

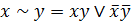; (6.10)

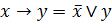; (6.11)

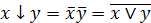; (6.12)

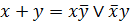; (6.13)

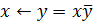; (6.14)

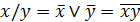. (6.15)

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3

Упражнение 1. Преобразовать логическую формулу

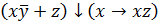
в формулу булевой алгебры и упростить ее. Результат проверить, сравнивая таблицы истинности заданной формулы и полученной формулы.

Выполнение.

,

,

=

,

,

,

= .

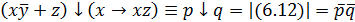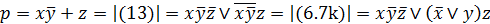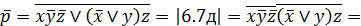
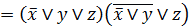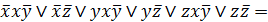
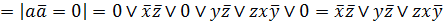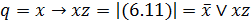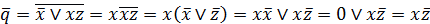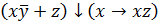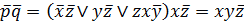Таблицы истинности.

Заданная формула.

.

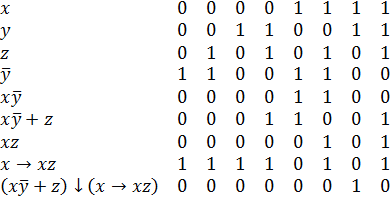Полученная формула булевой алгебры:

.

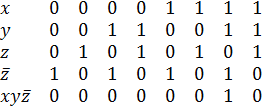ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Вариант	Логическое выражение
1.	.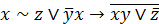
2.	.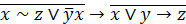
3.	.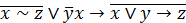
4.	.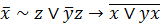
5.	.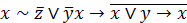
6.	.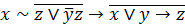
7.	.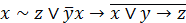
8.	.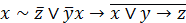
9.	.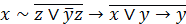
10.	.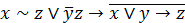
11.	.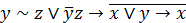
12.	.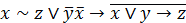
13.	.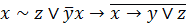
14.	.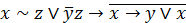
15.	.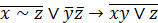
16.	.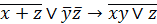
17.	.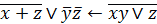
18.	.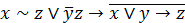
19.	.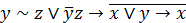
20.	.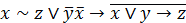
21.	.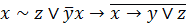
22.	.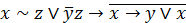
23.	.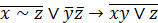
24.	.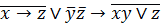
25.	.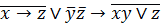

7. АЛГЕБРА ЖЕГАЛКИНА

Из определения операции сложения по модулю 2 можно убедиться в таких ее свойствах, легко доказуемых с помощью таблиц истинности:

– коммутативность:

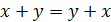, (7.1)

– ассоциативность:

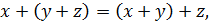(7.2)

– приведение подобных слагаемых:

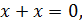(7.3)

– законы действий с константой 0:

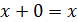, (7.4)

– дистрибутивность конъюнкции относительно сложение по модулю 2:

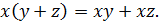(7.5)

Множество 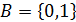, на котором определены операции конъюнкции со свойствами (6.1к – 6.6к) и сложение по модулю 2 со свойствами (7.1 ― 7.5) называется алгеброй Жегалкина.

В алгебре Жегалкина аддитивной операцией является операция сложения по модулю 2, мультипликативной ― операция конъюнкции. Алгебра Жегалкина ― абелево кольцо з единицей. Нейтральный элемент относительно сложения по модулю 2 ― константа 0, а симметричный элемент к элементу x ― сам элемент х. Нейтральный элемент относительно конъюнкции ― константа 1, симметричного элемента к элементу х не существует

Существование обратного элемента относительно сложения по модулю 2 дает возможность просто решать уравнения сложением по модулю 2 одинаковых элементов к обеим частям уравнений.

/*Пример 7.1

Уравнение 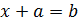(х ―неизвестное, a, b ―заданы) решается так:

,

,

. */

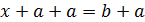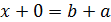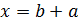Возможность решения таких уравнений, которая отсутствует в булевой алгебре, обусловило широкое применение операции сложения по модулю 2, например, для кодирования данных.

Любая булева функция может быть задана формулой булевой двухэлементной алгебры (в такие формулы могут содержать операции отрицание, конъюнкции и дизъюнкции). Аналогично, любая булева функция может быть задана формулой алгебры Жегалкина. Для преобразования формулы булевой алгебры в формулу алгебры Жегалкина можно использовать такие тождества

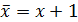, (7.6)

которое доказывается с помощью таблицы истинности, и

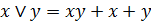, (7.7)

которое можно доказать аналитически:

.

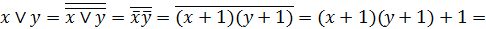
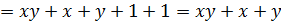/*Пример 7.2

Преобразовать формулу булевой алгебры

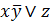
в формулу алгебры Жегалкина.

Выполнение.

.

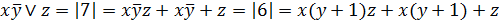Окончательно:

. */

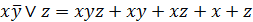ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4

Упражнение 1. Преобразовать логическую формулу

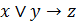
в формулу алгебры Жегалкина.

Выполнение.Преобразуем исходную логическую формулу в формулу булевой алгебры:

.

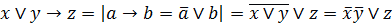А теперь в формулу алгебры Жегалкина:

.

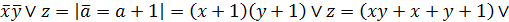
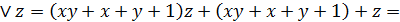
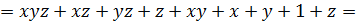
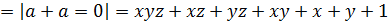Окончательно:

.

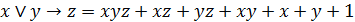ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ