Примеры решения задач к контрольной работе

1. Задание. Определить постоянную времени апериодического звена с коэффициентом передачи 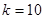, если частота среза его ЛАЧХ .

.

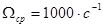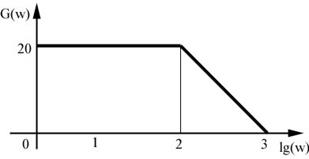
Решение

Коэффициент передачи звена в децибелах 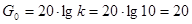. Частота среза в декадах 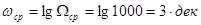. Так как ЛАЧХ апериодического звена имеет наклон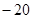 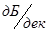,то частота сопряжения 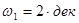. Следовательно постоянная времени апериодического звена .

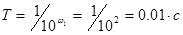Ответ: 0,01.

2. Задание. Указать величину наклона ЛАЧХ с передаточной функцией 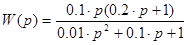при частоте .

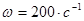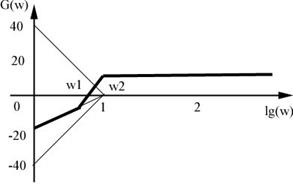
Решение:

САУ содержит следующие типовые звенья: дифференци­рующее с коэффициентом пере­дачи 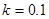, форсирующее с по­стоянной времени 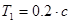и колебательное с постоянной времени 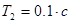с и коэффици­ентом демпфирования .

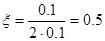Определим частоты сопряжения для построения асимптотической ЛАЧХ САУ.

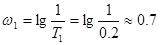и .

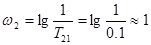При 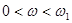ЛАЧХ (рис. ) имеет наклон 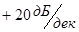, обусловленный дифференцирующим звеном. При 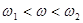наклон ЛАЧХ равен сумме наклонов ЛАЧХ дифференцирующего ( 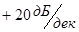) и форсирующего ( 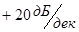) звеньев, то есть 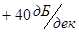. При 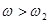“включается” колебательное звено, коэффициент наклона ЛАЧХ для которого равен 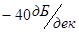при 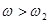. Суммарный наклон ЛАЧХ при частоте 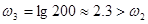будет равен .

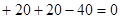Ответ: 0.

2. Задание. Определить значение 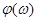при фиксированном значении частоты 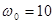для САУ, заданной передаточной функцией 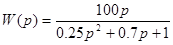(ответ привести в градусах с точностью до десятых).

Решение:

САУ состоит из двух типовых звеньев: дифференцирующего ( 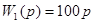), для которого фаза 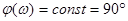, и колебательного 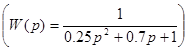с постоянной времени 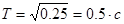и коэффициентом демпфирования 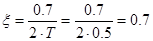, для которого фазовая характеристика рассчитывается по выражению .

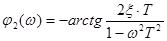При 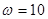получим:

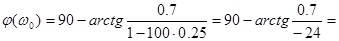
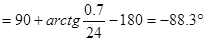
Ответ: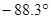

3. Задание. Задание последовательность наклонов ЛАЧХ: 0 на уровне 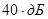при ,

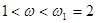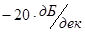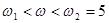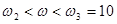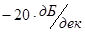при , при , при 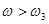. Восстановить передаточную функцию САУ по этим данным, представив ответ в виде дроби с полиномами в числителе и знаменателе, записанным в порядке убывания степени оператора Лапласса .

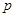Решение:

В соответствии заданными наклонами ЛАЧХ и частотами сопряжения, САУ содержит следующие последовательно соединенные звенья: пропорциональное (усилительное, безинерционное) с коэффициентом передачи 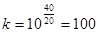; апериодическое (инерционное) с постоянной времени 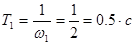; форсирующее с постоянной времени 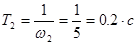; апериодическое (инерционное) с постоянной времени .

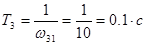Передаточная функция САУ будет иметь вид:

.

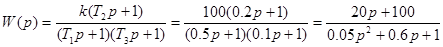Ответ: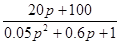

4. Задание.Определить граничное значение коэффициента коэффициента передачи САУ,

заданной структурной схемы рис.

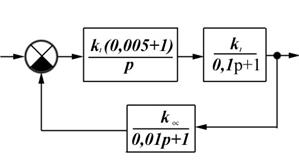
Решение:

Граничный коэффициент передачи заданной САУ наиболее целесообразно рассчитывать по критерию устойчивости Гурвица или Михайлова. Для этого необходимо определить передаточную функцию замкнутой САУ.

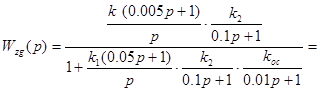
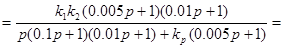
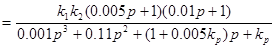
, где 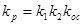– коэффициенты передачи разомкнутой САУ.

Характеристический полином САУ .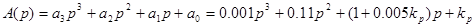

Определить граничное значение 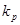по критерию Гурвица, в соответствии с которым на границе устойчивости для САУ 3–го порядка должно выполняться равенство: 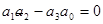, или 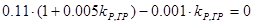, отсюда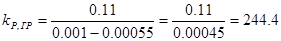

Ответ: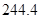

1. Задание. Апериодическое звено с параметрам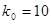и и 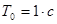охвачено положительной обратной связью 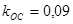. Определить коэффициент передачи 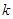и постоянную времени 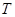эквивалентного апериодического звена.

Решение:

Передаточная функция звена, охваченного положительной обратной связью, имеет вид:

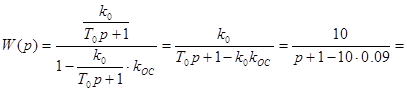
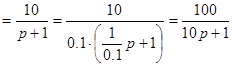, то есть , .

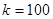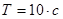Ответ: 100,10.

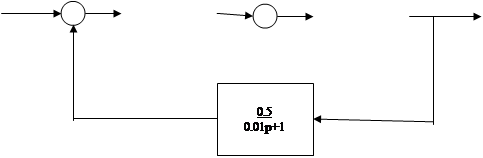
6. Задание. Определить величину выходного напряжения Uвых в установившемся режиме при возмущающем воздействии 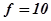и неизменном задающем воздействии Uвх=20 В в САУ, структурная схема которой приведена на рис. 4.7.

f

5 0.1p+1

10(0,005p+1) p+1

U_вх U_вых

Решение:

Определим передаточные функции САУ:

а) разомкнутой по задающему воздействию

;

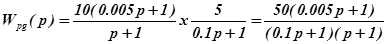б) разомкнутой по возмущающему воздействию ;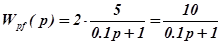

в) замкнутой по задающему воздействию

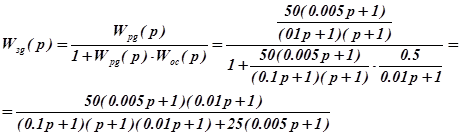
г) замкнутой по возмущающему воздействию

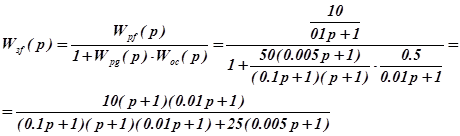
В установившемся (статическом) режиме при :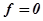

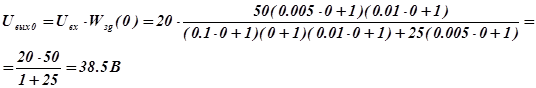
В установившемся (статическом) режиме при :

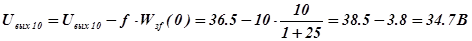
Ответ: 34,7

.

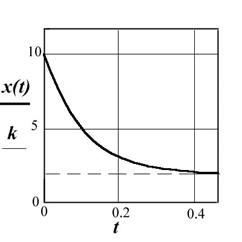
7. Задание. По ЛАЧХ звена, приведенной на рис. ,определить вид переходной чарактеристики на выходе этого звена.

Решение:

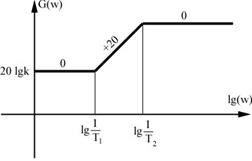
ЛАЧХ, приведенная на рис. Соответствует инерционному форсирующему звену с передаточной функцией 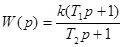, причем 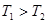. При подаче на вход звена единичного ступенчатого воздействия изображение выходной величины 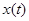будет .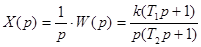

Найдем оригинал от этого изображения, воспользовавшись формулой разложения [ ] для нулевого и одного простого полюса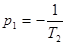

.

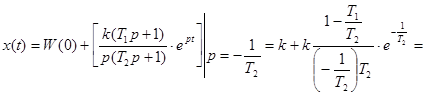
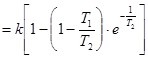На рис. приведен график 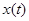, рассчитанный пр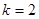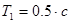и , и 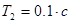. Зависимость 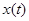имеет вид падающей экспоненты, начинающейся со значения 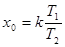и стремящейся к значению 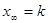. Аналогичную зависимость необходимо выбрать из предлагаемы вариантов.

Иванова Ирина Александровна