Матрицы. Действия над матрицами
Определители.
Пусть 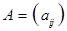 квадратная матрица порядка
квадратная матрица порядка 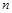 . Всякой такой матрице можно поставить в соответствие число
. Всякой такой матрице можно поставить в соответствие число 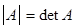 , называемое определителем этой матрицы, которое удовлетворяет следующим условиям:
, называемое определителем этой матрицы, которое удовлетворяет следующим условиям:
1) 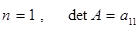 ; 2)
; 2) 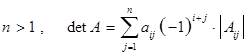 ,
,
где 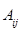 – квадратная матрица порядка
– квадратная матрица порядка 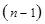 , получающаяся из матрицы
, получающаяся из матрицы 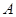 вычеркиванием
вычеркиванием 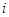 –й строки и
–й строки и 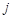 –го столбца. Определитель
–го столбца. Определитель 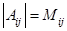 называется минором порядка
называется минором порядка 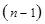 матрицы
матрицы 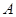 . Условия 1, 2 дают рекуррентное определение определителя матрицы.
. Условия 1, 2 дают рекуррентное определение определителя матрицы.
Определитель обладает следующими свойствами:
1) 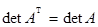 ;
;
2) при перестановке двух столбцов (строк) меняется знак определителя;
3) определитель матрицы, имеющей два одинаковых столбца (две одинаковые строки), равен нулю;
4) общий множитель столбца (строки) можно вынести за знак определителя (отсюда следует, что если один из столбцов (одна из строк) матрицы 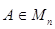 состоит из нулей, то
состоит из нулей, то 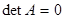 );
);
5) если к элементам некоторого столбца (строки) матрицы А прибавить соответствующие элементы другого столбца (другой строки), предварительно умноженные на одно и то же число, то определитель новой матрицы В будет равен 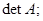
6) если какой-либо столбец (какая-либо строка) является линейной комбинацией других столбцов (других строк) матрицы А, то 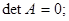
7) обозначим через 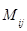 определитель матрицы порядка
определитель матрицы порядка 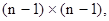 получающейся из матрицы
получающейся из матрицы 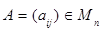 путем зачеркивания i-й строки и j-го столбца; число
путем зачеркивания i-й строки и j-го столбца; число 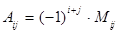 называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента 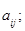 для любого k,
для любого k, 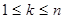 справедливы равенства:
справедливы равенства:
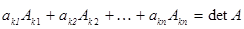 ,
, 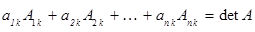
(разложение определителя по k-му столбцу);
8) 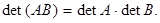
Пользуются и другим обозначением определителя матрицы 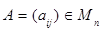 :
:
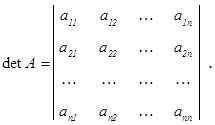
Определитель второго порядка вычисляется по формуле
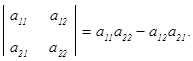
Определитель третьего порядка вычисляется по формуле
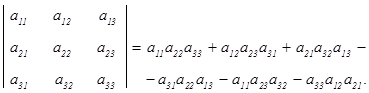
Для вычисления определителя третьего порядка лучше пользоваться правилом Саррюса или правилом «3  5».
5».
+ – 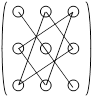 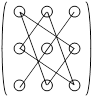 а б Рис. 1 а б Рис. 1 |  Рис. 2 Рис. 2 |
Правило Саррюса использует схему, изображенную на рис. 1. Правило состоит в том, что девять чисел, составляющих определитель, разбиваются на шесть троек по схеме (каждый элемент участвует дважды). Каждой тройке придается знак «+», если элементы, входящие в нее, расположены на главной диагонали или в вершинах равнобедренного треугольника с основанием, параллельным главной диагонали (рис.1, а), или «–», если элементы, входящие в тройку, расположены на побочной диагонали или в вершинах равнобедренного треугольника с основанием, параллельным побочной диагонали (рис.1, б) (побочная диагональ тянется справа-сверху-влево-вниз). Затем берется сумма произведений элементов троек с учетом их знаков.
Правило «3 ´ 5» использует следующую схему (к матрице  добавлены первые два столбца). Элементы матрицы соединены шестью отрезками, как показано на рис.2. Произведению элементов, составляющих тройку и лежащих на одном отрезке, придается знак «+», если отрезок параллелен главной диагонали, и «–», если отрезок параллелен побочной диагонали. Определитель A равен сумме произведений элементов троек с учетом их знаков.
добавлены первые два столбца). Элементы матрицы соединены шестью отрезками, как показано на рис.2. Произведению элементов, составляющих тройку и лежащих на одном отрезке, придается знак «+», если отрезок параллелен главной диагонали, и «–», если отрезок параллелен побочной диагонали. Определитель A равен сумме произведений элементов троек с учетом их знаков.
Определитель треугольной, в том числе и диагональной матрицы равен произведению элементов главной диагонали:
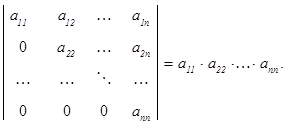
Для вычисления определителя иногда оказывается удобным приведение матрицы к треугольному виду с использованием свойств определителя.
Матрицы. Действия над матрицами
Матрицей порядка 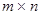 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел
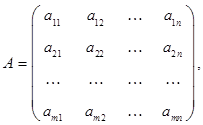
состоящая из m строк и n столбцов, рассматриваемая как единый алгебраический объект, над которым могут производиться определенные алгебраические действия. Часто пишут
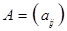 ,
, 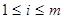 , 1
, 1 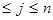 . Множество всех матриц порядка
. Множество всех матриц порядка 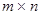 обозначим
обозначим 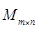 , множество всех квадратных матриц порядка
, множество всех квадратных матриц порядка 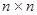 – через
– через 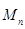 .
.
Произведением матрицы 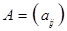
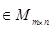 на число
на число 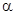 (действительное или комплексное) называют матрицу
(действительное или комплексное) называют матрицу 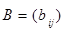
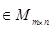 , определяемую по правилу
, определяемую по правилу 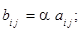 при этом пишут
при этом пишут 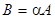 .
.
Суммой  матриц
матриц 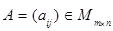 ,
, 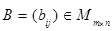 называют матрицу
называют матрицу 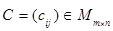 , определяемую по правилу
, определяемую по правилу 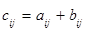 ; при этом пишут
; при этом пишут 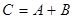 . Складывать можно лишь матрицы одинакового порядка.
. Складывать можно лишь матрицы одинакового порядка.
Произведением матрицы 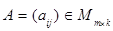 на матрицу
на матрицу 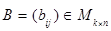 называют матрицу
называют матрицу 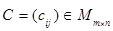 , элементы которой определяются по правилу
, элементы которой определяются по правилу 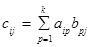 ; при этом пишут
; при этом пишут 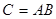 . Произведение матриц определено, если количество столбцов первого множителя А совпадает с количеством строк второго множителя В. (Можно сказать, что элемент
. Произведение матриц определено, если количество столбцов первого множителя А совпадает с количеством строк второго множителя В. (Можно сказать, что элемент 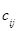 матрицы
матрицы 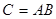 есть результат скалярного произведения i-й строки матрицы А на j-й столбец матрицы В.)
есть результат скалярного произведения i-й строки матрицы А на j-й столбец матрицы В.)
Введенные операции над матрицами обладают всеми известными свойствами суммы и произведения чисел
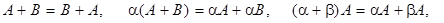
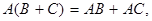
кроме одного: вообще говоря, 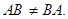
Матрицу
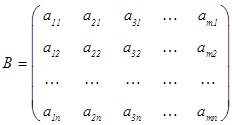
называют транспонированной к матрице А и пишут 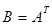 ;
; 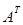 получается из А переменой местами столбцов и строк.
получается из А переменой местами столбцов и строк.
Нулевой матрицей (нуль-матрицей) называется матрица 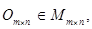 состоящая из нулей.
состоящая из нулей.
Единичной матрицей порядка 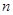 называется квадратная матрица
называется квадратная матрица 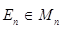 , на главной диагонали которой, тянущейся слева-сверху-вправо-вниз, находятся единицы, а остальные элементы равны 0:
, на главной диагонали которой, тянущейся слева-сверху-вправо-вниз, находятся единицы, а остальные элементы равны 0:
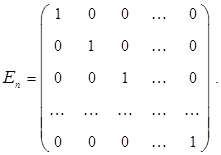
Часто пишут просто Е, опуская индекс n там, где это не приводит к недоразумению.
Матрицы О и Е играют роль нуля и единицы: 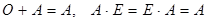 (операции считаются дозволенными).
(операции считаются дозволенными).
Квадратная матрица, у которой все элементы вне главной диагонали равны 0, называется диагональной. Квадратная матрица, у которой все элементы, расположенные ниже главной диагонали, равны 0, называется треугольной.
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения и понятия.
1.Вычислить определитель:
1) 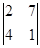 .
.
Решение. 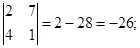
2) 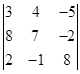 .
.
Решение. 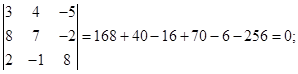
3) 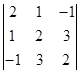 .
.
Вычисление определителя с помощью понижения его порядка.
Вычисление определителя порядка выше третьего следует вычислять путем последовательного сведения этого определителя к низшему порядку, разлагая его по элементам какой-либо строки или столбца. Формула разложения определителя по строке (столбцу) принимает особенно простой вид, когда в этой строке (столбце) все элементы равны нулю, кроме одного 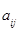 . Тогда определитель равен произведению элемента
. Тогда определитель равен произведению элемента 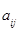 на алгебраическое дополнение этого элемента
на алгебраическое дополнение этого элемента 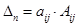 .
.
4) 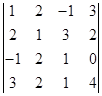 .
.
Решение. Умножим первую строку на два и вычтем из второй 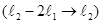 . Сложим первую и третью строки и поставим на место третьей строки
. Сложим первую и третью строки и поставим на место третьей строки 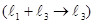 , умножим первую строку на три и вычтем из четвертой строки
, умножим первую строку на три и вычтем из четвертой строки 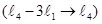 . Получим
. Получим
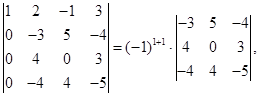
Сложим вторую и третью строки
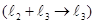
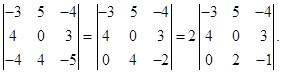
Ко второму столбцу прибавим третий, умноженный на два 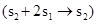 :
:
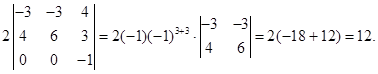
Можно записывать так:
5) 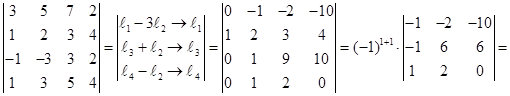
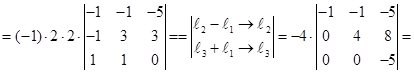
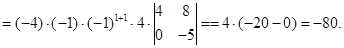
6) 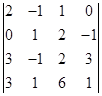 ; 7)
; 7) 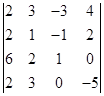 ; 8)
; 8) 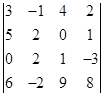 .
.
Ответ. 1) –25; 2) 0; 3) –20; 4) 0; 5) -70; 6) -80;
7) 48; 8) 223.
2.Вычислить 3A – 2BC, если:
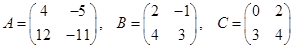 .
.
Ответ. 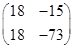 .
.
3.Вычислить:
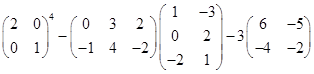 .
.
Ответ. 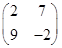 .
.
4.Вычислить: а) 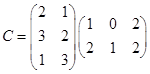 ; б)
; б) 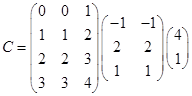 .
.
Ответ. а) 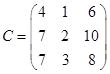 ; б)
; б) 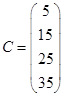 .
.
