Задачи к 2-ой части экзамена
Базовая часть экзамена
I. Понятийный блок
1. Отображение (функция).
2. Предел последовательности.
3. Предел функции.
4. Непрерывность функции в точке и на множестве.
5. Равномерная непрерывность на множестве.
6. Производная функции.
7. Функции, монотонные на промежутке.
8. Точка внутренняя экстремума.
9. Выпуклые функции.
10. Точка перегиба графика функции.
11. Асимптоты графика функции.
12. Первообразная для функции 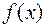 на промежутке.
на промежутке.
13. Неопределённый интеграл.
14. Интеграл Римана.
15. Верхний и нижний интегралы Дарбу.
16. Несобственный интеграл с верхним бесконечным пределом.
17. Несобственный интеграл от неограниченной функции.
18. Абсолютная и условная сходимость несобственных интегралов.
19. Квадрируемые фигуры.
20. Кубируемые тела.
21. Длина дуги кривой.
II.Фактический блок.
1. Формула Тейлора для многочлена. Формула Тейлора для произвольной функции с остаточным членом в форме Лагранжа (без доказательства).
2. Достаточное условие монотонности функции.
3. Необходимое условие существования внутреннего экстремума функции.
4. Достаточное условие существования внутреннего экстремума функции в терминах первой производной.
5. Достаточное условие выпуклости вверх и вниз графика дважды дифференцируемой функции.
6. Достаточное условие существования точек перегиба графика функции.
7. Основное свойство первообразной функции.
8. Основные свойства неопределенного интеграла.
9. Необходимое условие интегрируемости.
10. Свойства верхних и нижних интегральных сумм.
11. Свойства верхнего и нижнего интегралов Дарбу (без доказательства).
12. Критерий интегрируемости в терминах верхних и нижних интегральных сумм (без доказательства).
13. Интегрируемость непрерывных функций.
14. Линейность интеграла Римана.
15. Аддитивность интеграла Римана (без доказательства).
16. Монотонность интеграла Римана.
17. Интегрируемость модуля интегрируемой функции и оценка модуля интеграла.
18. Первая теорема о среднем значении для интеграла (без доказательства).
19. Непрерывность интеграла с верхним переменным пределом (без доказательства).
20. Дифференцируемость интеграла с верхним переменным пределом (без доказательства).
21. Формула Ньютона – Лейбница.
22. Теорема о замене переменной в определённом интеграле для случая непрерывности подинтегральной функции. 
23. Критерий Коши сходимости несобственных интегралов.
24. Достаточные условия сходимости несобственных интегралов (признаки сравнения).
25. Площадь криволинейной трапеции.
26. Длина дуги кривой (без доказательства).
27. Объём тела вращения.
28. Площадь поверхности вращения (без доказательства).
III.Алгоритмический блок.
1. Исследование функции и построение графика.
2. Интегрирование рациональной дроби.
3. Интегрирование дробно – линейных иррациональностей.
4. Интегрирование квадратичных иррациональностей.
5. Интегрирование биномиальных дифференциалов.
6. Интегрирование некоторых тригонометрических выражений.
7. Алгоритм доказательства тождеств, связывающих дифференцируемые функции.
IV. Операционный блок.
1. Представление простейших элементарных функций формулой Тейлора:
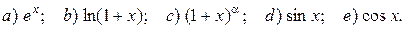
2. Отыскание наибольшего и наименьшего значения функции на отрезке: 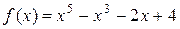 на
на 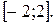
3. Исследование функций и построение графика: 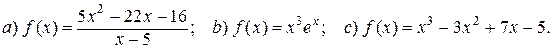
4. Отыскание множества значений функции: 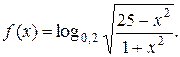
5. Вычисление интегралов: 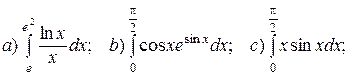
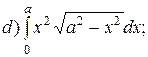
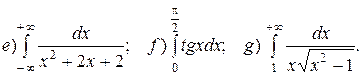
6. Вычисление площади плоской фигуры:
а) найдите площадь фигуры, ограниченной графиками функций 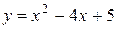 и
и 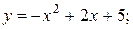
б) найдите площадь фигуры, ограниченной графиком функции 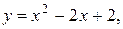 касательной к этому графику в точке
касательной к этому графику в точке 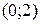 и прямой
и прямой 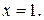
7. Вычисление объёма тела вращения: найдите объём тела вращения, образованного вокруг оси 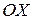 фигуры, ограниченной кривой
фигуры, ограниченной кривой 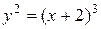 и прямой
и прямой 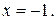
8. Применение методов дифференциального и интегрального исчисления к решению задач:
а) найдите наибольший член последовательности 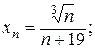
б) найдите все 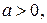 для каждого из которых
для каждого из которых 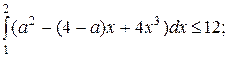
в) в множестве функций 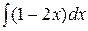 найдите ту, для которой число 1,5 является наибольшим значением;
найдите ту, для которой число 1,5 является наибольшим значением;
г) для функции 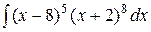 найдите точки экстремума и точки перегиба.
найдите точки экстремума и точки перегиба.
9. Исследование несобственных интегралов на сходимость: 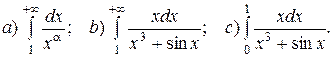
II уровень
1. Формула Тейлора с остаточным членом в форме Лагранжа и Коши.
2. Достаточные условия экстремума функции в терминах производных высших порядков.
3. Верхний и нижний интегралы Дарбу и их свойства.
4. Первый критерий интегрируемости.
5. Второй критерий интегрируемости.
6. Интегрируемость монотонной функции.
7. Интегрируемость функции, множество точек разрыва которой можно покрыть конечным набором интервалов сколь угодно малой длины.
8. Аддитивность интеграла Римана.
9. Монотонность интеграла, первая теорема о среднем значении для интеграла.
10. Свойства интеграла с верхним переменным пределом.
11. Длина дуги.
12. Кубируемые тела. Объём тела вращения.
13. Пример Шварца. Площадь поверхности вращения.
14. Условная сходимость несобственного интеграла с верхним бесконечным пределом. Признаки сходимости.
15. Формула Тейлора с остаточным членом в форме Пеано.
16. Множества меры нуль в смысле Лебега. Критерий Лебега интегрируемости функции по Риману (без доказательства). Интегрируемость композиции непрерывной и интегрируемой функции.
17. Интегрирование по частям в определённом интеграле и формула Тейлора.
18. Замена переменной в определённом интеграле (общий случай).
19. Вторая теорема о среднем значении для интеграла.
20. Признаки абсолютной сходимости несобственных интегралов от неограниченных функций.
21. Условная сходимость интеграла от неограниченных функций. Признаки сходимости.
Задачи к 2-ой части экзамена
1. Найдите 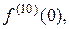 если
если
а) 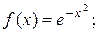 б)
б) 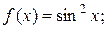 в)
в) 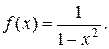
2. Найдите:
а) 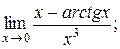 в)
в) 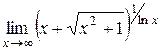 ;
;
г) 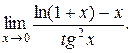
3. При каких значениях параметра 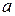 функция
функция 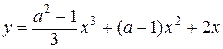 возрастает на всей числовой прямой?
возрастает на всей числовой прямой?
4. Найдите все значения параметра 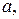 при каждом из которых функция
при каждом из которых функция 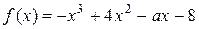 возрастает на интервале
возрастает на интервале 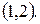
5. Докажите неравенства:
а) 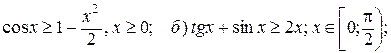
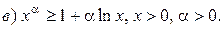
6. Найдите пределы последовательностей:
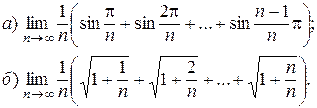
7. Вычислите интегралы: 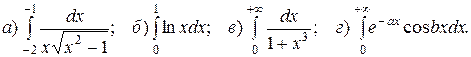
8. Найдите пределы: 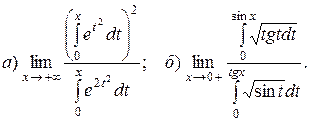
9. Исследуйте на абсолютную и условную сходимость 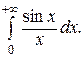
10. Найдите значения параметра 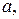 при которых точка
при которых точка 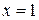 является минимумом функции
является минимумом функции 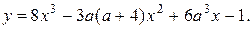
11. Найдите значение 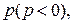 при котором площадь фигуры, образуемой параболой
при котором площадь фигуры, образуемой параболой 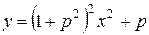 и прямой
и прямой 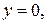 была бы наибольшей.
была бы наибольшей.
12. Докажите, что функция 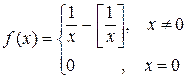 интегрируема на
интегрируема на 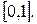
13. Докажите неравенство 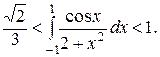
14. При каждом значении параметра 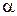 исследуйте интеграл
исследуйте интеграл 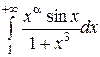 на абсолютную и условную сходимость.
на абсолютную и условную сходимость.
15. Справедлива ли формула Лагранжа на 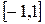 для функции
для функции 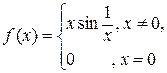 ?
?
16. Пусть 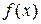 - чётная, дважды непрерывно дифференцируемая функция,
- чётная, дважды непрерывно дифференцируемая функция, 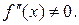 Докажите, что
Докажите, что 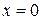 - точка экстремума функции
- точка экстремума функции 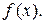
17. Докажите, что у дважды дифференцируемой функции между точками экстремума лежит, по крайней мере, одна точка перегиба.
18. Приведите пример функции, определённой на 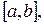 непрерывной на
непрерывной на 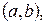 но не интегрируемой на
но не интегрируемой на 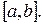
19. Приведите пример неинтегрируемой функции, квадрат которой есть функция интегрируемая.
20. Постройте график функции 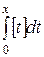 на отрезке
на отрезке 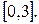
21. Объясните, почему неверно равенство 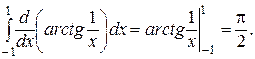
22. Докажите, что между двумя действительными корнями многочлена с действительными коэффициентами имеется корень его производной.
