Рактическое занятие №1. Расчёт параметров конструкций, определяющих функциональные свойства сцепления автомобиля.

Цель занятия - освоение методики расчёта параметров сцепления автомобилей.

1.

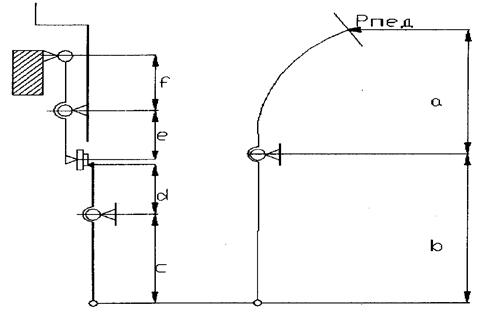Определение передаточного отношения привода сцепления.

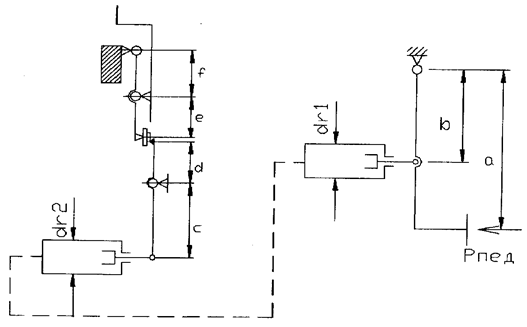Рис.1. Механический привод сцепления.

Рис.2. Гидравлический привод сцепления.

Общее передаточное число привода сцепления U _{п с} =U₁*U₂,

где U₁ - передаточное число педального привода;

U₂ - передаточное число рычагов включения сцепления.

U₁=(a*c)/(b*d); U₂=e/f; U _{п с} =(a*c*e)/(b*d*f). (1)

2.2. Гидравлический привод сцепления (рис. 2)

U₁=(a*c*d_г2²)/(b*d*d_г1²); U₂=e/f; U_пс=(a*c*e*d_г2²)/(b*d*f*d_г1²) (2)

3. Методика расчёта параметров сцепления (рис. 3).

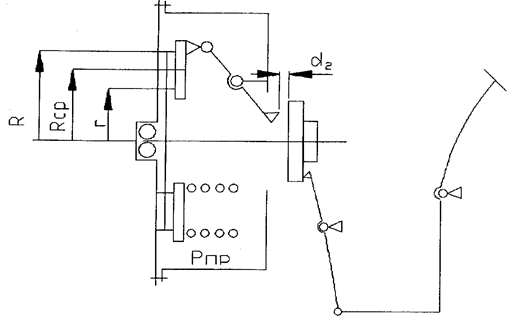Рис.3. Включение сцепления.

3.1. Наружный и внутренний диаметры ведомого диска рассчитываются в том случае, если производиться проектировочный расчёт, т. е. эти параметры неизвестны:

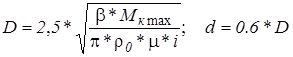где М _{к max} - максимальный момент двигателя;

b - коэффициент запаса сцепления в зависимости от типа сцепления и а/м. изменяется в пределах от 1,2...2,5;

m - расчётный коэффициент трения (0,3);

r₀ - давление на фрикционные накладки (0,15...0,25 МПа); меньшие значения имеют сцепления грузовых а/м.;

i - число поверхностей пар трения.

Полученные размеры уточняются по ГОСТ 1787 - 80.

3.2. Момент, передаваемый сцеплением

М_с=М _{к max} *b=Р_пр*m*R_ср*i,

где R_ср=(R+r)/2

3.3. Потребное усилие пружин

Р_пр=М _{к max} *b/m*R_ср*i (3)

4. Расчёт параметров цилиндрических пружин

4.1. Усилие, создаваемое одной пружиной

Р_пр’=Р_пр/Z, (4)

где Z - число пружин, которое должно быть кратным числу рычагов, а усилие одной пружины Р^/_пр не должно превышать 800 Н.

4.2. Диаметр проволоки

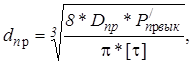где Р^/_пр.вык=(1,1...1,2) Р^/_пр - усилие пружины в выключенном состоянии сцепления;

D_пр - средний диаметр витка;

[t]=700...900 МПа - допустимое напряжение для сталей 65Г, 85Г.

4.3. Число рабочих витков пружины

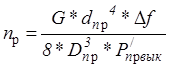где G=8*10⁴ МПа - модуль упругости;

Df=(d*i+d₁) - дополнительная деформация пружины при выключении сцепления.

Зазор d между поверхностями трения при выключении сцепления равен 0,75...1 мм - для однодискового сцепления и 0,5...0,75 - для двухдискового сцепления.

Деформация d₁ ведомого диска при включенном сцеплении равна 1,0...1,05 мм - для упругого диска и 0,15...0,25 мм - для неупругого диска.

4.4. Полное число витков пружины

n _п =n _р +(1.2...2).

4.5. Деформация пружины при включенном сцеплении

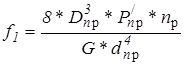4.6. Жёсткость пружины

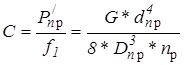для легковых а/м. С=30...40 Н/мм

для грузовых а/м С=20...40 Н/мм

По результатам расчётов строится упругая характеристика пружины сцепления а/м (рис. 4).

На рис.4. представлена упругая характеристика пружины сцепления а/м, имеющего М _{к max} = 402 Нм. Параметры сцепления следующие: b=2,15; D=342 мм; d=186 мм; Z=16; d=0,9 мм; d₁=0,2 мм; l=2; D _пр =25 мм; Р_пр.вык^/=1,1*Р_пр^/; [t]=800 МПа; d_пр=3,9 мм; С=34,15 Н/мм.

5. Расчёт двойных пружин.

5.1. Результирующее усилие двойной пружины

Р^/_пр=Р₁+Р₂.

5.2. Принимается допущение об одинаковых деформациях (f₁=f₂) и напряжениях (t_{max 1}=t_{max 2}) в обеих пружинах.

5.3. Задаётся жёсткость пружин:

С=Р^/_пр /f=(Р₁+Р₂)/f.

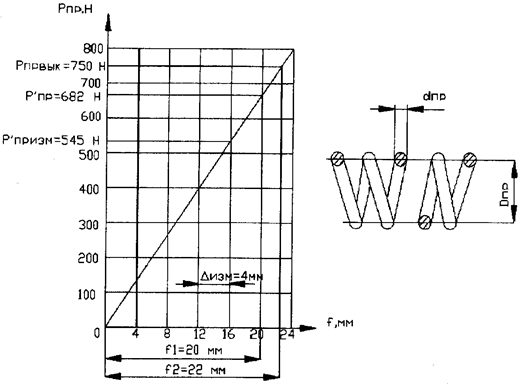Рис. 4. Упругая характеристика пружины сцепления.

5.4.

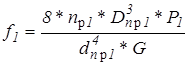Находиться связь между деформацией и другими параметрами пружин:

5.5.

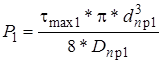Выражается Р₁ через t_max1:

5.6.

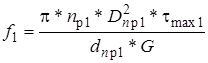Подставляя это значение в выражение для f₁, получают

5.7. Аналогично

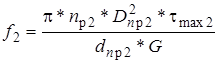5.8.

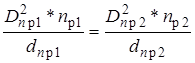Из допущения, что f₁=f₂ и t_max1=t_max2, следует условие подбора параметров внешней и внутренней пружин:

Параметры двойной пружины подбирают, задаваясь конструктивными значениями D_пр1 и D_пр2 и варьируя значениями n_р1, n_р2, d_пр1 и d_пр2, учитывая, что Р^/_пр=Р₁+Р₂.

Например, параметры пружины сцепления а/м ГАЗ - 24:

усилие одной пружины, Н 260 220

средний диаметр, мм 28,5 21,5

диаметр проволоки, мм 3

жёсткость, Н/мм 6,2 10,7

6. Расчёт диафрагменной пружины.

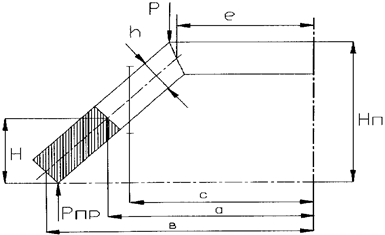На рис. 5 приведена расчётная схема для определения параметров диафрагменной пружины.

Рис. 5 Расчётная схема диафрагменной пружины.

Расчёты ведутся в предположении недеформированности сечения пружины.

6.1. Усилие пружины (нажимное усилие на ведомый диск)

,

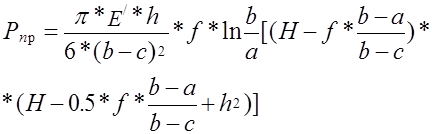
где Е^/=Е/(1-m²), (Е - модуль упругости I рода; Е=2*10⁵ МПа; m - коэффициент Пуассона; m=0,26);

h - толщина;

H - высота сплошной части пружины;

а, b, с, е - геометрические размеры;

f - деформация пружины в месте приложения силы Р_пр. Параметры пружины находятся в пределах:

h=2...2,5 мм - для легковых а/м.;

h=3...5 мм - для грузовых а/м.;

H/h=1,5...2; b/c=1,2...1,5; b/e=2.5; b/h=75...100; число лепестков n=8...20.

При известных геометрических параметрах пружины, задавая деформацию f (с интервалом в 2 мм), рассчитывают соответствующие значения Р_пр. По результатам расчётов строиться упругая характеристика пружины и по заданным параметрам двигателя и сцепления определяется потребная деформация пружины во включённом f₁ и выключенном f₂ состоянии.

На рис. 6 представлена упругая характеристика пружины, имеющей следующие геометрические размеры:

b=100 мм; а=75,5 мм; с=72 мм; е=25 мм;

H_п=9 мм; H=4,5 мм; h=2,2 мм; n=18.

Эта пружина установлена в сцеплении, имеющем следующие параметры:

D=200 мм; d=142 мм; d=1 мм; d₁=1 мм; b=1,4 мм; М _{к max}=89,3 Нм.

Для обеспечения потребного усилия пружины во включённом состоянии сцепления в соответствии с графиком (рис. 6) необходима предварительная деформация пружины f₁=5,6 мм. Деформация пружины при выключенном сцеплении f₂=8,6 мм

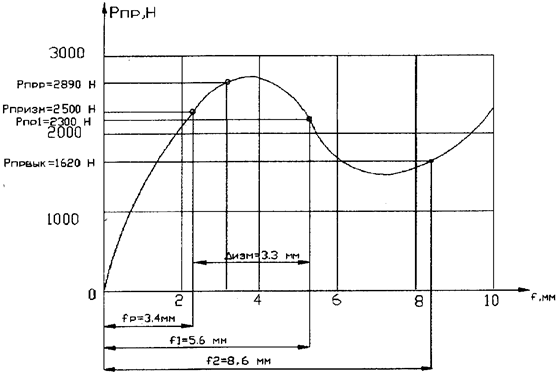Рис. 6. Упругая характеристика пружины.

7. Расчёт гасителя крутильных колебаний.

Этот расчёт связан с решением сложной задачи колебаний трансмиссии. В этой связи ограничиваются подбором гасителя. При этом на основании анализа существующих конструкций конструктивные параметры можно принимать следующие:

n число пружин Z_г=6...8;

n диаметр проволоки d_прг=3...4 мм;

n средний диаметр витка D_прг=16...18 мм;

n полное число витков n_пг=5...6;

n жёсткость пружин С_г=100...300 Н/мм;

n момент трения фрикционных элементов М_трг=20...100 Нм;

n момент предварительной затяжки пружин М_пр=(0,15...0,2) М _{к max};

n усилие, сжимающее одну пружину:

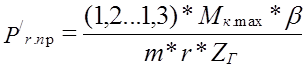
где r - радиус приложения усилий к пружине;

m - число ведомых дисков.

[t_max]=700...900 МПа

7.1. Ступица ведомого диска.

Проверяется:

а) на смятие шлиц [б_см]=15...30 МПа (150..300 кг*с/см²);

б_см=Р/(F*a), где Р=М _{к max} *b/r_ср; r_ср=(d _нар +d _вн )/4;

F=(d _нар -d _вн )*l*i/2,

где l - длина шлиц, i - число шлиц,

a=0,75 - коэффициент точности прилегания шлиц.

б) на срез шлиц

t=Р/i*l*b*a, где b - ширина шлиц, [t]=5...15 МПа (50...150 кг*с/см²).

Шлицы выполняются прямобочными и эвольвентными.

Материал ступицы: ст. 35, ст. 40Х.

Ведомый диск обычно изготавливают из пружинной стали.

7.2. Накладки ведомого диска.

Требования к накладкам:

* высокий коэффициент трения, мало изменяющийся от температуры, удельного давления, скорости;

* высокие механические свойства: прочность (в том числе и от разноса при n=2*n_max об/мин.), износостойкость;

* хорошая теплопроводность;

* плавное, пропорциональное нажимной силе, нарастание силы трения.

Для а/м сцеплений применяют в основном асбестовые накладки (асбест, наполнители и связующие). Асбест обладает хорошей термической и химической стойкостью.

Наполнители органические и неорганические, смоляные частицы увеличивают износостойкость.

Металлы - Сu, латунь, бронза, Al (порошок, стружка, куски проволоки) - улучшают теплопроводность и плавность включения. Zn - стабилизирует m. Pb - уменьшает износ, задиры, но ухудшает стойкость при повышении температуры. Графит увеличивает износостойкость.

Связующие определяют фрикционные свойства, износостойкость и термическую устойчивость. Применяют фенолформальдегидные смолы и их модификации и синтетические каучуки, а также комбинации смол и каучуков.

Накладки выполняют формованными, навитыми и тканными.

Формованные накладки применяют на большинстве грузовых а/м.

Примерный состав: асбест 40% (в виде коротких волокон),

наполнители 30...40%

связующие 20...30%.

Навитые накладки применяют главным образом на легковых а/м. (ЗАЗ, ВАЗ, АЗЛК).

Примерный состав: асбест -50%

проволока -10%

хлопок -10%

наполнители -5...10%

связующие -20%

Тканые накладки применяют на грузовых (ГАЗ) и легковых а/м.

Практическое занятие №2. Нагрузки в коробке передач автомобиля

Цель работы - освоение методики определения нагрузочных параметров и расчёта элементов коробки передач.

1. Нагрузки в коробке передач.

Рассмотрим простейшую схему 3-х вальной коробки передач при включении одной передачи и схему сил, действующих на зубчатые колёса и валы (рис. 1).

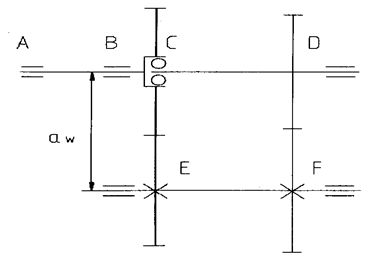Рис. 1. Схема коробки передач.

На зубья пары постоянного зацепления привода промежуточного вала действуют следующие силы:

· окружная Р_пз=М _{к max}/r _{w пз};

· осевая (при косозубых колёсах) Р _{х пз} =Р_пз*tgb;

· радиальная Р_{R пз}=Р_пз*tg(a_w)/cosb;

· нормальная Р _{п п з} =Р_пз/cos(a_w)_*cosb,

где a_w - угол профиля зуба;

b - угол наклона зубьев;

r _{w пз} - радиус делительной окружности шестерни ведущего вала.

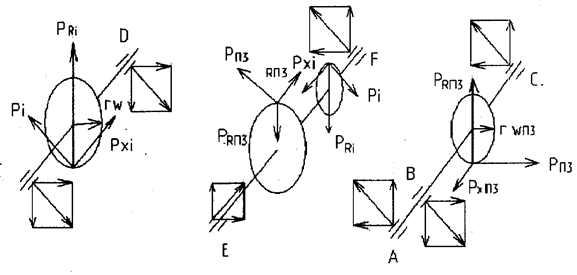Ведомый вал Промежуточный вал Ведущий вал

При включении i-й передачи на зубья пары действуют силы:

· окружная Р _i =M _{k max} *u _i/r _{w i};

· осевая Р _{х i} =Р_i*tgb;

· радиальная Р_{R i}=Р_i.*tg(a_w)/cosb;

· нормальная Р _{п i}=Р_i./cos(a_w)_*cosb;

здесь u_i - передаточное число включённой передачи;

r_{w i} - радиус делительной (начальной) окружности зубчатого колеса ведомого вала.

В современных конструкциях 2-х вальных коробок передач уравновесить осевые силы невозможно и они полностью воспринимаются подшипниковыми узлами.

В 3-х вальных коробках осевые силы уравновешиваются на промежуточном валу на всех передачах, кроме 1-й и задней (если они выполнены на прямозубых колёсах). На рис. 2 представлена схема сил, действующих на зубчатые колёса промежуточного вала на одной передаче.

Исходя из равенства осевых сил:

Р _{х 1}=Р _{х 2}; Р _х.1 =Р₁*tgb₁; Р _х.2 =Р₂*tgb₂;

Р₁=М _{k max} *u _{п з}/r _w1; Р₂=М _{k max} *u _{п з}/r _w2,

где u _{п з} - передаточное число пары постоянного зацепления,

r _w1, r _w2 - радиусы делительных (начальных) окружностей колёс промежуточного вала.

Из приведённых уравнений:

tgb₁ / tgb₂= r _w1 / r _w2

Если модули колёс одинаковы, то tgb₁ / tgb₂=Z₁/Z₂,

Определив реакции валов на каждой передаче, строят эпюры моментов и определяют изгибающий и крутящий моменты, а затем результирующее напряжение (рис. 3).

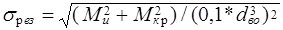
где d _{в о} - диаметр вала в опасном сечении.

2. Жесткость валов КПП

Жёсткость валов определяют по их прогибу. Прогиб вала в каждой плоскости не должен превышать 0,1 мм.

Полный прогиб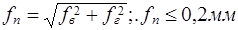

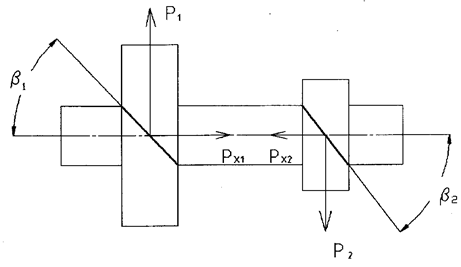Шлицы валов проверяют на смятие, [t _см ]=200 МПа.

Рис. 2. Промежуточный вал.

1.) Реакции в опорах валов

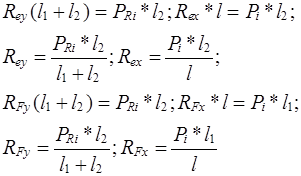
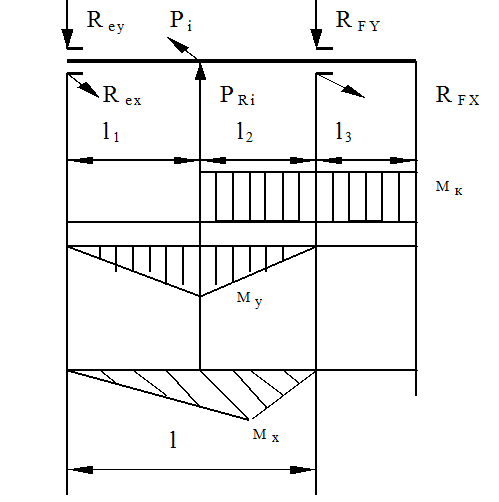2). Изгибающие моменты в опасном сечении под шестернёй:

Рис. 3. Расчётная схема и эпюры моментов.

а). от силы Р_i (в горизонтальной плоскости)

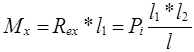
б). от силы Р_{R i} (в вертикальной плоскости)

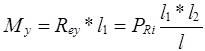
3). Результирующий момент в опасном сечении

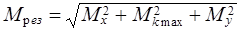
4.) Результирующее напряжение

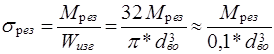
Для круга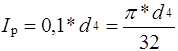

Для кольца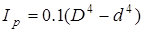

Напряжения в валах в силу их большой жёсткости не должны превышать 400 Мпа.

Валы большой протяжённости проверяют на скручивание по формуле:

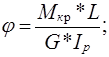
[j]=0,35⁰

G*I_p – жёсткость при кручении;

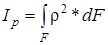- полярный момент, см⁴.

3. Подбор подшипников коробки передач.

Подбор подшипников производиться с учётом долговечности Т, которая должна соответствовать пробегу а/м до капитального ремонта

Т=S/V _{а ср.}

где S – пробег до капремонта, км;

V _{а ср.} – средняя техническая скорость а/м;

n для легковых а/м V _{а ср.}=35…40 км/ч;

n для грузовых а/м V _{а ср.}=30…35 км/ч.

Пробег до капремонта основных агрегатов составляет:

n легковые а/м малого класса 125…150 тыс. км;

n легковые а/м среднего класса 200…250 тыс. км;

n грузовые а/м и автобусы 200…350 тыс. км.

При определении эквивалентной нагрузки необходимо знать продолжительность работы а/м на передачах (см. таблицу).

Таблица

Тип а/м	Передачи
Легковые	0,1 0,01	2 0,6	5 3,1	83 91,4	––
Грузовые	0,1 0,01	1 0,2	3 1,4	10 7,8	80 87,3
Самосвалы	10 1,4	16 6,5	25 21,5	25	15
Автопоезда	0,5 0,05	3 0,4	5 2,7	20 18,3	70 77,2

Примечание: в числителе указано время в %, в знаменателе - пройденный путь в %.

В общем случае V _{а ср.}=0,6*V _{а max} .

Связь между долговечностью Т и числом циклов L

L=60*T*n/10⁶.

Эквивалентная динамическая нагрузка, воспринимаемая радиальными и радиально-упорными шарикоподшипниками для каждой передачи:

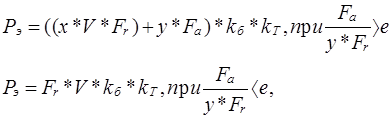
где х, y - коэффициенты радиальной и осевой нагрузок;

е - параметр осевых нагрузок;

F_r, F_a - радиальная и осевая нагрузки, определяемые по расчётному моменту Мр;

к_б - коэффициент безопасности, учитывающий влияние динамических нагрузок от неровностей дороги; к_б=1 - для коробок передач;

к_т - температурный коэффициент;

V - коэффициент вращения (при вращении внутренней обоймы V=1, внешней V=1,2);

x, y, e - выбирают по каталогу.

Эквивалентное число циклов подшипника L^/_i на каждой передаче

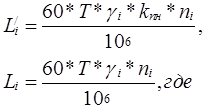
L_i - фактическое число циклов;

n_i - частота вращения кольца подшипника на i - й передаче (n _i =n_M/u_T);

n_M - частота вращения первичного вала, соответствующая средней скорости движения;

u_Т - передаточное число от первичного до рассчитываемого вала;

g_i - доля работы на i - й передаче (по таблицам);

k_{пн i} - коэффициент пробега для i - й передачи.

Номинальная долговечность подшипника

L=(C/P _э )^P.

где С - динамическая грузоподъёмность (выбираемая по каталогу). С=Р_э *L^1/р;

Р - степенной показатель (для шариковых подшипников Р=3,для роликовых подшипников Р=3,3);

Р_э - эквивалентная динамическая нагрузка на подшипник.

4. Форма отчёта.

4.1. Привести схему рассчитываемого вала с указанием размеров и действующих сил и моментов.

4.2. Привести эпюры изгибающих, крутящих моментов и перерезывающих сил.

Практическое занятие №3. Механизмы дифференциалов автомобилей

Цель работы - изучение принципиальных схем дифференциалов , оценка их конструкций.

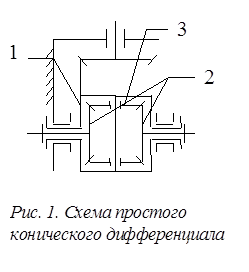1. Конструктивные схемы дифференциалов.

1.1. Простой конический дифференциал (рис. 1) состоит из картера (коробки) 1, двух полуосевых шестерен 2, двух (легковые а/м) или четырех (грузовые а/м) сателлитов 3. Шестерни 2 соединяются с полуосями шлицами, либо выполняются заодно. Трущиеся поверхности разъединяются антифрикционными шайбами.

Особенности:

- коэффициент блокировки К_б=М_от/М_заб=1 (трение малое);

- простота устройства, малые габариты, надежность, высокий КПД;

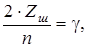- число зубьев полуосевых шестерен 2 и сателлитов 3 может быть четным и нечетным и должно подчиняться условию сборки

где Z_ш - число зубьев полуосевой шестерни;

n - число сателлитов;

g - целое число.

- обеспечивает устойчивость при движении по скользкой дороге и торможении двигателем благодаря равным крутящим моментам на ведущих колесах;

- ограничивает проходимость.

1.2. Простой конический дифференциал с принудительной блокировкой (рис. 2)

Особенности:

- при включении блокирующей муфты 4 ;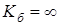

- момент включения определяется водителем;

- при движении по скользкой дороге - потеря устойчивости.

1.3. Пульсирующий шестеренчатый дифференциал.

Включает те же элементы (детали) , что и простой конический дифференциал. Отличие заключается в профиле зубьев. В обычном (Д) окружное усилие постоянно по величине , т. к. полюс зацепления не меняет своего положения и линия зацепления имеет постоянный наклон под углом зацепления независимо от относительного положения зубьев зацепляющихся колес и их четного или нечетного числа.

В пульсирующем дифференциале (рис. 3) профиль зубьев специальный: линия зацепления меняет наклон, а полюс зацепления перемещается. При этом окружное усилие изменяется и зависит от относительного положения зубьев. Число зубьев должно быть обязательно нечетным. Условия сборки те же, что и у обычного дифференциала.

Особенности:

- коэффициент блокировки К_б - переменный: его величина изменяется за поворот сателлита на 1 зуб от

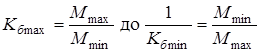K_{б max}=2 ... 2.5

- наиболее простой из самоблокирующихся (Д);

- высокий КПД;

- из-за малого коэффициента блокировки не обеспечивает значительного повышения проходимости;

- при вращении сателлита создается пульсация момента в трансмиссии.

1.4. Дифференциал свободного хода (обгонный) (рис. 4).

При таком (Д) нет жесткой кинематической связи между полуосями. При разных скоростях вращения колес крутящий момент передается через одно колесо; буксуют оба колеса, буксование одного колеса невозможно.

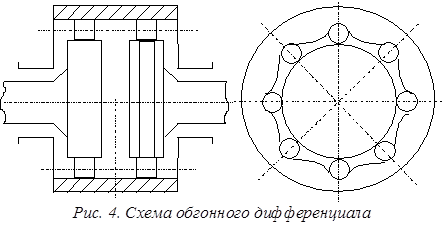Различают дифференциалы свободного хода роликовые (рис. 4) и с кулачковыми муфтами (рис. 5).

Особенности:

- коэффициент блокировки ;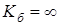

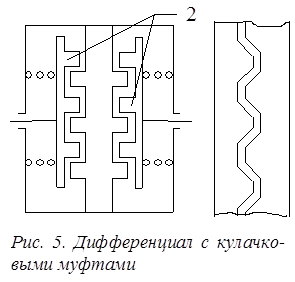- учитывая, что дифференциал работает постоянно (неровности дороги, разный износ шин, неодинаковая нагрузка на шины), крутящий момент постоянно передается через одно из колес, что вызывает повышенный износ шин, вследствие не прямой зависимости износа от передаваемого момента;

- роликовый (Д) прост по устройству, сепараторы роликов могут поворачиваться друг относительно друга на небольшой угол, при этом ролики обгоняющей полуоси - свободны;

- большие удельные давления, что является недостатком.

В кулачковом (Д) происходит выключение полуосевых муфт обгоняющей полуоси. Кулачки обгоняющей муфты 2 выходят из зацепления с кулачками ведущего кольца 1 за счет набегания зубьев концентрично расположенного зубчатого кольца муфты на зубья того же профиля, расположенные концентрично ведущему кольцу. Удельные давления в кулачковом (Д) меньше, чем в роликовом;

- при расчете (Д) свободного хода на каждую полуось прикладывается полный момент, подводимый к коробке дифференциала.

1.5. Дифференциал повышенного трения.

Этот дифференциал может выполняться шестеренчатым , червячным, кулачковым (сухарным).

Коэффициент блокировки К_б этих Д - в связи с их КПД.

Для симметричного дифференциала

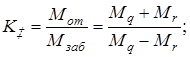но

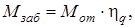
поэтому

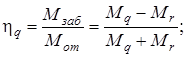т.е. K_б=1/h_q.

1.6. Шестеренчатый дифференциал с постоянным моментом трения (рис. 6).

Особенности:

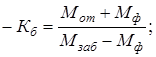- коэффициент блокировки К_б - переменный, т.к. момент трения муфты М_ф=const.

С увеличением передаваемого момента К_б - уменьшается;

- при малом значении М_ф дифференциал малоэффективен, при большом М_ф - снижается КПД трансмиссии.

Шестеренный дифференциал может быть выполнен с моментом трения, пропорциональным передаваемому моменту. Крестовина такого (Д) составлена из 2-х частей , которые при передаче М_кр раздвигаются, скользя концами шипов по наклонным вырезам коробки (Д). Чем больше передаваемый момент, тем сильнее сжимаются муфты. У такого (Д)

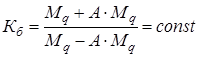А - коэффициент пропорциональности.

К_б= 3...4.

1.7. Кулачковые (сухарные) дифференциалы.

Кулачковые дифференциалы конструктивно могут выполняться с горизонтально (рис. 7-а) и радиально (рис. 7-б) расположенными сухарями. Сухари могут размещаться в один или два ряда.

На схеме (рис. 8) представлено кинематическое взаимодействие элементов кулачкового дифференциала. При этом принято: V_д - линейная скорость обоймы 1 корпуса дифференциала; V_л, V_п - линейное скорости звездочек 2 и 3 левой и правой полуосей.

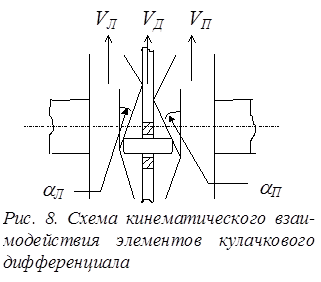Предположим, что V_п>V_д>V_л, а a_л=a_п, тогда относительная скорость звездочки левой полуоси

V_л'=V_д-V_л.

Относительная скорость звездочки правой полуоси

V_п'=V_п-V_д.

Учитывая, что a_л=a_п, V_п'=V_л' и V_л+V_п=2·V_д.

Если все углы a_л >< a_п, что характерно для однорядного несимметричного дифференциала с неравным числом кулачков, уравнение кинематики имеет вид

V_л+V_п=2·V_д-(V_л'-V_п').

На кулачках отстающей полуоси скорость скольжения сухаря направлена в сторону вращения ведущего элемента, а на кулачках забегающей полуоси - в противоположную сторону. Поэтому силы трения увеличивают момент, передаваемый на отстающую полуось и уменьшают момент, передаваемый на забегающую полуось.

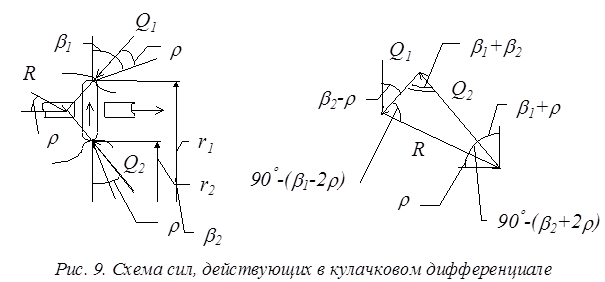
Со стороны кулачков забегающей (внешней) и отстающей (внутренней) звездочек на сухарь действуют силы Q₁ и Q₂, вызывающие реакцию R со стороны обоймы корпуса дифференциала на сухарь (рис. 9). Силы Q₁ и Q₂ направлены под углом трения r к общей нормали к сопряженным поверхностям.

Для забегающей полуоси r вычитается из угла давления b₁, а для отстающей - r складывается с углом давления b₂.

Моменты на полуосях:

М_от=Q₂·r₂·sin(b₂+r)

M_заб=Q₁·r₁·sin(b₂-r).

Из треугольника сил имеем

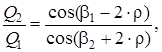поэтому коэффициент блокировки

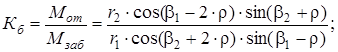В имеющихся конструкциях К_б=4...5.