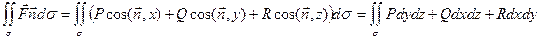Поверхностные интегралы второго рода

Поверхностный интеграл первого рода есть поверхностный интеграл от скалярной функции.

Пусть теперь на поверхности σ задана некоторая векторная функция

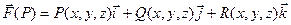
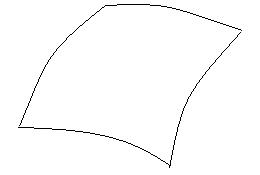
Определим интеграл от этой функции по поверхности σ. Но в этом случае важно по какой стороне поверхности провести интегрирование. Сторону поверхности можно указать, проведя в произвольной т. Р единичный вектор нормали .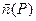

Разобьем поверхность σ на n площадок ∆σ_i, на каждой из них возьмем произвольную т. Р_i и рассмотрим сумму

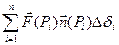(1)

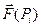–значение вектора 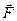в т.Р_i

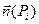–единичный вектор нормали в этой точке

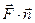–скалярное произведение этих векторов.

Предел суммы (1) при maxΔσ_i→0 называется поверхностным интегралом второго рода и обозначается cимволом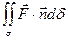

Таким образом

n → → → →

lim ∑ F_i·n_i ∆ σ _i = ∫∫ F·n d σ (2)

i=1 σ

max _Δσ _i→0

Каждое слагаемое суммы

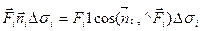(3)

равно объему цилиндра с основанием ∆ σ_i и высотой F_i cos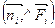

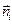
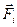
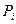
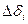
Если вектор 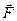есть скорость жидкости, протекающей через поверхность σ, то произведение (3) равно количеству жидкости, протекающей через площадку ∆σ_i за единицу времени в направлении вектора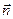

Поверхностный интеграл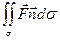

представляет собой общее количество жидкости, протекающей через поверхность σ за единицу времени в положительном направлении.

Итак, если под вектором 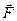подразумевать вектор скорости течения жидкости, то

→

поверхностный интеграл (2) называется потоком векторного поля F через поверхность σ.

Из определения поверхностного интеграла следует, что если поверхность σ разбить на части σ ₁, σ ₂, …, σ _n, то

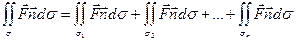
Единичный вектор 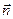имеет вид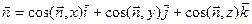

Тогда

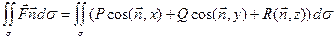(2)

где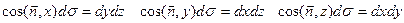

представляют проекции площадки ∆δ на координатные плоскости

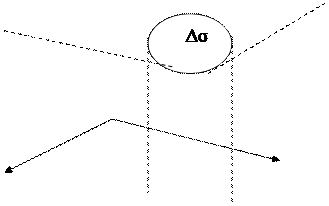
z

→

n

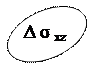∆δ_xz

x y

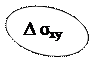
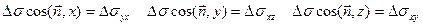
На основании этого поверхностный интеграл записывают в другой форме