Основные характеристики функции

СОДЕРЖАНИЕ

Глава I. ФУНЦИЯ И ЕЕ ПРЕДЕЛ

§ 1. Множества............................................................................................................................ 2

§ 2. Понятие функции................................................................................................................ 4

§ 3. Основные характеристики функции................................................................................. 5

§ 4. Классификация функций.................................................................................................... 6

4.1. Обратная функция........................................................................................................ 6

4.2. Сложная функция......................................................................................................... 7

4.3. Основные элементарные функции и их графики..................................................... 8

§ 5. Числовые последовательности........................................................................................... 10

§ 6. Предел функции.................................................................................................................. 12

6.1. Предел функции в точке.............................................................................................. 12

6.2. Предел функции при 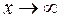................................................................................... 13

6.3. Теоремы о пределах функций..................................................................................... 13

6.4. Два замечательных предела......................................................................................... 14

§ 7. Бесконечно большие и бесконечно малые функции....................................................... 16

7.1. Бесконечно большие функции и их свойства.......................................................... 16

7.2. Бесконечно малые функции и их свойства............................................................... 16

7.3. Связь между функцией, ее пределом и бесконечно малой функцией.................... 17

7.4. Сравнение бесконечно малых функций.................................................................... .18

§ 8. Вычисление пределов функций......................................................................................... 19

§ 9. Непрерывность функции.................................................................................................... 21

9.1.Односторонние пределы............................................................................................... 21

9.2. Понятие непрерывности функции............................................................................. 21

9.3. Классификация точек разрыва функции.................................................................... 22

9.4. Свойства функций, непрерывных на отрезке........................................................... 24

Глава II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

§ 10. Понятие производной, ее геометрический и физический смысл................................ 25

10.1. Определение производной..................................................................................... 25

10.2.Геометрический смысл производной..................................................................... 26

10.3. Физический смысл производной........................................................................... 27

§ 11. Правила дифференцирования функций и производные элементарных

функций.............................................................................................................................. 27

11.1. Правила дифференцирования................................................................................ 27

11.2. Производные элементарных функций................................................................... 28

11.3. Логарифмическое дифференцирование............................................................... .30

11.4. Производные высших порядков............................................................................ 31

11.5. Производная неявной функции............................................................................. 32

11.6. Производная функции, заданной параметрически.............................................. 33

§ 12. Дифференциал функции................................................................................................... 33

§ 13. Основные теоремы дифференциального исчисления................................................... 33

§ 14. Правило Лопиталя............................................................................................................. 37

14.1. Теорема Лопиталя..................................................................................................... 37

14.2. Другие виды неопределенностей и их раскрытие................................................ 38

§ 15.Исследование функций при помощи производных...................................................... 39

15.1. Признак монотонности функции. Необходимое условие

экстремума функции................................................................................................ 39

15.2. Достаточные условия экстремума......................................................................... 40

15.3. Направление выпуклости и точки перегиба графика функции.......................... 41

15.4. Асимптоты графика функций................................................................................. 42

15.5. Общая схема исследования функции .................................................................... 43

15.6. Наибольшее и наименьшее значения функции на отрезке.................................. 45

Литература................................................................................................................................... 46

Глава I. ФУНКЦИЯ И ЕЕ ПРЕДЕЛ

Множества

1.Множеством называется совокупность, система, семейство некоторых объектов, объединенных по какому-либо признаку. Например, множество студентов университета, множество корней уравнения, множество натуральных чисел.

Обозначаются множества заглавными буквами латинского алфавита: .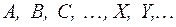

Объекты, из которых состоит множество, называются элементами множества.

Элементы множества обозначаются соответственно строчными буквами латинского алфавита: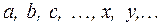

Например, 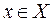– элемент 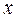принадлежит множеству 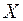; 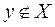–элемент 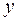не принадлежит множеству ;

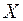Множество, не имеющее ни одного элемента, называется пустым множеством. Пустое множество обозначается так: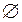

Элементы множества записываются в фигурных скобках, в которых они перечислены или в скобках может быть указано свойство, которым обладают все элементы данного множества.

Например, 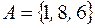– множество 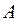состоит из трех чисел 1, 8, 6 ; 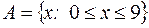– множество 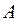состоит из всех действительных чисел, удовлетворяющих неравенству .

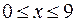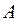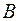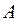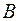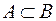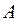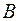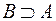Множество называется подмножеством множества , если каждый элемент множества является элементом множества . Обозначается подмножество так: ( включено в ) или (множество 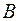включает в себя множество ).

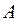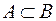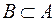Множества, состоящие из одних и тех же элементов, называются равными множествами. Если и , то 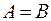, следовательно, говорят, что множества 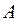и 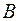равны илисовпадают.

Объединением (или суммой) множеств 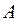и 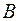называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному их этих множеств. Записывают 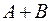или .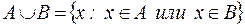

Пересечением (или произведением) множеств 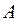и 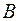называется множество, состоящее из элементов, каждый из которых одновременно принадлежит множеству 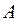и множеству 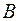. Записывают 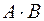или .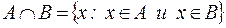

Разностьюмножеств 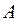и 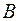называется совокупность тех элементов 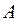, которые не содержатся в 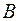. Записывают .

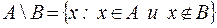2. Для сокращения записей используются некоторые логические символы:

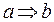- следует, т.е. из предложения 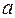следует предложение ;

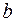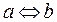- равносильно, т.е. 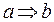и ;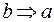

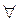- для любого, для всякого;

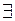- существует, найдется;

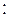- имеет место, такое что;

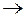- соответствие.

Например, 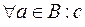– для любого элемента 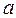из множества 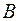имеет место предложение 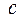; 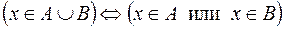объединение множеств 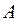и .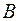

3. Множества, элементами которых являются числа, называются числовыми множествами.

Например:

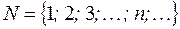– множество натуральных чисел;

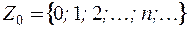– множество целых неотрицательных чисел;

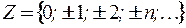– множество целых чисел;

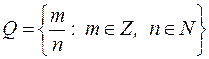– множество рациональных чисел;

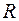– множество действительных чисел.

Между этими множествами существует соотношение .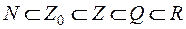

Множество 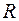содержит рациональные и иррациональные числа. Всякое рациональное число выражается дробью.

Например:

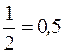– ( конечная десятичная дробь); 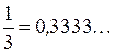– (бесконечная периодическая дробь).

Действительные числа, не являющиеся рациональными, называются иррациональными числами. Это бесконечные непериодические дроби.

Например, , .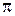

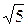4.Пусть 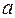и 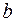– действительные числа, причем .

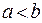Числовыми промежутками (интервалами) называются подмножества всех действительных чисел, имеющих следующий вид:

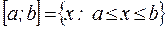– отрезок (сегмент, замкнутый промежуток);

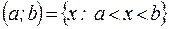– интервал (открытый промежуток);

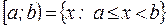		– полуоткрытые интервалы;
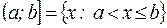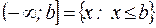	– бесконечные интервалы;

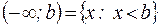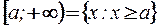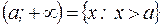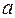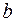Числа и называются соответственно левым и правым концами промежутков. Символы 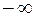и 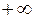не числа, это символическое обозначение неограниченного удаления точек числовой оси от начала 0 влево и вправо.

Пусть точка 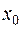–любое действительное число (точка на числовой прямой).

Окрестностью точки 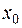называется любой интервал 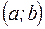, содержащий точку .

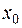Интервал 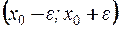, где 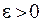, называется 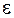–окрестностью точки 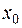,число 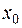– центр интервала, число 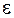– радиус интервала.

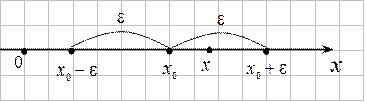
Если 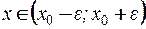, то выполняется неравенство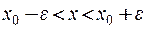

.

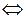
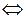
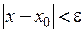Это означает попадание точки 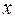в 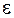– окрестность точки .

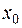Понятие функции

Одним из основных понятий математики является понятие функции. Оно связано с установлением зависимости (связи) между элементами двух множеств.

Определение. Если каждому элементу 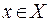соответствует единственный элемент 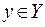, то говорят, что на множестве 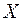задана функция 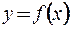( 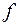- знак функции).

Переменную 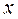называют аргументом или независимой переменной, а переменную 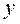– зависимой переменной от х; множество 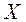– областью определения функции 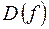, а множество 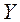– множеством значений функции 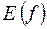, 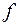– закон соответствия. 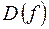– множество значений аргумента, при которых формула 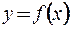имеет смысл.

Кроме буквы 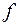для обозначения функций используют и другие буквы греческого и латинского алфавитов: 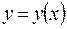, , 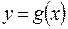, 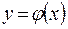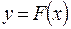и так далее.

Примеры.

1) , .

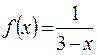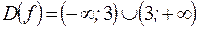2) , .

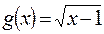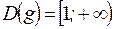3) 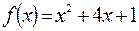или , .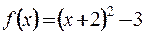

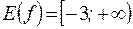4) , .

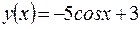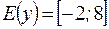Если элементами множеств 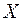и 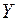являются действительные числа, то функция называется числовой.

Частное значение функции при 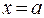обозначают так: .

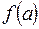Например,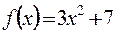

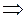
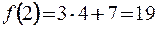
График функции 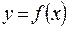– это множество точек плоскости с координатами 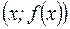, где 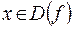, для каждой из которых 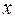является значением аргумента, а 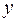является соответствующим значением функции.

Способы задания функции.

1. Аналитический: функция задается с помощью одной или нескольких формул, или уравнений.

Если область определения функции не указана, то она совпадает со множеством всех значений аргумента, при которых указанная формула имеет смысл.

2.Графический: задается график.

3.Табличный: с помощью таблицы ряда значений аргумента и соответствующих значений функции, полученных в результате некоторого опыта.

4.Словесный: функция описывается правилом ее составления.

Например, функция Дирихле 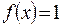, если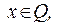

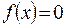, если 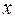– иррациональное.

Основные характеристики функции

1.Функция 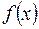, определенная на множестве 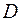, область опреления которой симметрична относительно начала координат, называется: четной, если 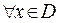выполняются условия 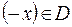и 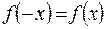; нечетной, если 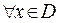выполняются условия 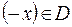и 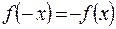. В противном случае функция 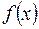называется функцией общего вида.

График четной функции симметричен относительно оси 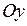, график нечетной функции симметричен относительно начала координат.

Например, функция 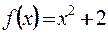- четная, а функция 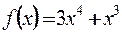–функция общего вида.

2. Пусть функция 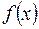определена на множестве 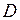, интервал .

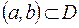Если для любых 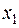и 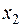из интервала 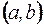, причем 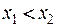, выполняется неравенство:

1) 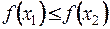, то функция 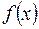называется неубывающей на ;

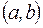2) 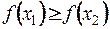, то функция 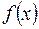называется невозрастающей на ;

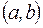3) 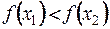, то функция 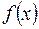называется возрастающейна ;

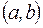4) 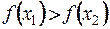, то функция 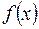называется убывающей на .

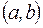Во всех рассмотренных случаях функции называются монотонными, авозрастающая и убывающая функции строго монотонными.

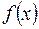Например, на рисунке функция на 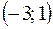строго монотонная;

на 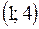монотонная.

3. Функция 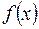, определенная на множестве 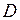, называется периодическойна этом множестве с периодом 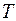, где 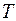– положительное число, если выполняются условия: 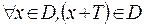и 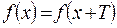. Если 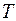– период, то периодом функции также будут числа 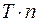, где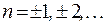

Например, для функции 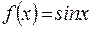периодами будут числа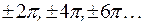

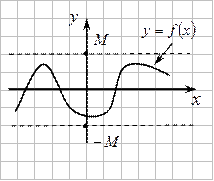
4. Функция 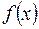, определенная на множестве 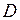, называется ограниченной на этом множестве, если существует такое число 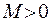, что для всех 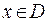выполняется неравенство 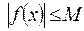. Коротко можно записать так:

.

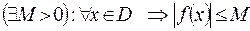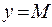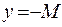График ограниченной функции расположен между прямыми и . Например, функция 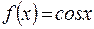ограничена, так как .

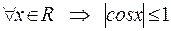Классификация функций

Обратная функция

Пусть 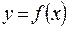функция от 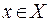с областью значений 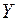. Пусть, кроме того, каждому значению 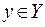соответствует только одно значение 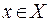. Тогда на множестве 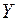определена функция 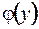с областью значений 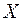, обладающая свойством 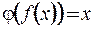для любого 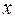из множества .

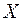Функция 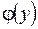называется обратной к функции 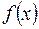. Если 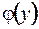– обратная функция к 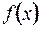, то функция 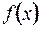– обратная функция к 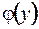. Про функци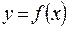и и 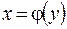говорят, что они являются взаимно обратными.

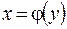Чтобы найти функцию , обратную к функции 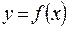, достаточно решить уравнение 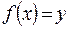относительно 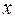. Традиционно независимую переменную обозначают 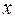, а зависимую .

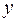Например, функци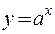и и 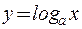взаимно обратные. Графики их симметричны относительно биссектрисы I и III координатных углов.

Из определения обратной функции следует, что для любой строго монотонной функции существует обратная. При этом если 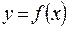возрастает, то и 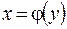также возрастает.

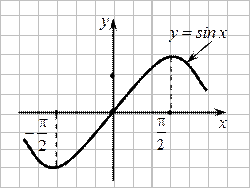
Например, функция 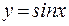на 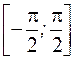строго возрастает.

На этом промежутке существует обратная ей функция 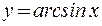, которая также возрастает.

Сложная функция

Пусть функция 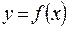определена на множестве 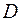, а функция 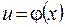определена на множестве 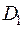, причем 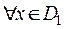соответствующее значение 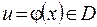. Тогда функция 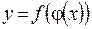, определенная на множестве 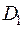, называется сложной функцией ( или суперпозицией заданных функций или функцией от функции) с аргументом .

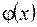Например, 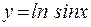– сложная функция, аргумент .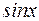