Задания для индивидуальной работы. По методу начальных параметров в предлагаемых задачах необходимо:
По методу начальных параметров в предлагаемых задачах необходимо:
Задача 8.9.1. –Определить прогиб и угол поворота сечения в т.В.

Задача 8.9.2. –Определить прогиб посредине балки и углы поворота на концах консолей.

Задача 8.9.3. –Определить проги б и угол поворота сечения в т.С.
 |

8.9.5 Вычисление перемещений балки энергетическими методами
Выше были рассмотрены аналитические методы определения перемещений в сечениях балки, и дающие точное решение задачи. Однако часто нас интересует не вся упругая линия балки, а только перемещения в каком-либо сечении. Тогда для определения прогиба или угла поворота балки удобно пользоваться другим подходом, часто используемым на практике. Такой подход основывается на применении энергетических методов, дающих в общем случае хотя и приближенные решения, но приемлемые с практической точки зрения Энергетические методы основываются на применении выражения для потенциальной энергии упругой деформации балки.
8.9.5.1. Потенциальная энергия упругой деформации балки при изгибе
Согласно закону сохранения энергии работа внешних сил А в положении равновесия тела равна потенциальной энергии его упругой де формации V:

В общем случае потенциальную энергию для балки можно вычислить так:

где 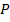 – обобщенная сила (сосредоточенная сила
– обобщенная сила (сосредоточенная сила 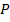 , внешний момент
, внешний момент 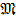 );
); 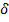 – соответствующее обобщенной силе обобщенное перемещение (прогиб 𝓌, угол поворота сечения балки
– соответствующее обобщенной силе обобщенное перемещение (прогиб 𝓌, угол поворота сечения балки 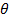 ).
).
Например, для случаев нагрузки балки (рис. 8.41):
 – обобщенные силы;
– обобщенные силы;
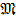 |
 – обобщенные перемещения.
– обобщенные перемещения. 
Рисунок 8.41 – Обобщенные силы и обобщенные перемещения для балки
Таким образом, термин «обобщенная сила» отвечает нагрузке, а соответствующее этой нагрузке перемещение называется «обобщенным перемещением».
При поперечном изгибе балки обычно пользуются следующим приближенным выражением для потенциальной энергии (без учета перерезывающих сил, что дает малую добавку):

где 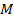 – изгибающий момент в сечении балки длиной l;
– изгибающий момент в сечении балки длиной l;
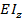 – изгибная жесткость балки.
– изгибная жесткость балки.
Использование выражения для потенциальной энергии упругой деформации балки (8.57) позволяет рассчитать перемещения в требуемом сечении балки х с помощью энергетических методов на основе:
а) теоремы Костильяно;
б) интеграла Мора;
в) графоаналитического способа Верещагина.
8.9.5.2. Теорема Кастильяно
Она формируется следующим образом: частная производная от потенциальной энергии по одной из независимых внешних сил равна перемещению, соответствующему этой силе.
Так, прогиб балки 𝓌 в точке приложения сосредоточенной силы Р (см.рис.8.41,а) равен:

а угол поворота сечения 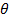 , где действует внешний момент
, где действует внешний момент 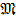 , вычисляется по формуле:
, вычисляется по формуле:

Рассмотрим применение теоремы Кастильяно для простейших случаев нагрузки балки.
Случай 1. Определить прогиб конца балки в т.В (рис.8.42).

Рисунок 8.42 – К определению прогиба балки на конце консоли
Решение
Изгибающий момент в сечении х балки равен:

а частная производная  . Тогда на основании выражения (8.58) прогиб балки в т.В будет равен:
. Тогда на основании выражения (8.58) прогиб балки в т.В будет равен:


Знак плюс в полученном выражении соответствует прогибу балки в направлении действия сосредоточенной силы Р.
Данный результат соответствует точному решению задачи, полученному путем интегрирования дифференциального уравнения упругой линии балки (см.п.8.9.2).
Случай 2. Определить угол поворота сечения в т.В балки (рис.8.43).

Рисунок 8.43 – К определению угла поворота сечения балки на опоре В
Решение
Изгибающий момент в сечении х балки равен:

где 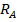 – реакция балки на опоре А, равная по условиям статики
– реакция балки на опоре А, равная по условиям статики

Тогда:

По формуле (8.59) имеем:


Знак плюс в выражении для 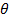 говорит о повороте сечения в т.В в направлении действия момента
говорит о повороте сечения в т.В в направлении действия момента 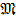 .
.
Примечание: 1. В данном методе прогиб балки в точке по ее оси можно определить только в случае приложения в точке сосредоточенной силы Р, а угол поворота сечения – только в случае приложения в месте сечения внешнего момента 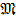 .
.
2. При нескольких участках внешней нагрузки, где уравнения для изгибающих моментов будут разными, интегрирование по формулам (8.58) и (8.59) необходимо проводить отдельно по каждому участку.
3. Если требуется найти перемещение в сечении балки, где не приложена соответствующая обобщенная сила, то в этом сечении мысленно прикладывается дополнительная обобщенная сила (  ), которая принимается равной нулю после дифференцирования по ней под знаком интеграла.
), которая принимается равной нулю после дифференцирования по ней под знаком интеграла.
8.9.5.3. Интеграл Мора
Интеграл Мора позволяет вычислять перемещения балок, если определение производных от изгибающего момента в выражениях теоремы Кастильяно заменить вычислением изгибающих моментов от единичной нагрузки  . Тогда перемещения балки рассчитываются по формулам:
. Тогда перемещения балки рассчитываются по формулам:


где 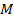 - выражение изгибающего момента на участке балки от заданных сил в принятом сечении;
- выражение изгибающего момента на участке балки от заданных сил в принятом сечении;  – выражение изгибающего момента в принятом сечении от действия силы
– выражение изгибающего момента в принятом сечении от действия силы  или единичного момента
или единичного момента 
Следовательно, производная от изгибающего момента по обобщенной силе – это то же самое, что и изгибающий момент от единичной силы.
Так, для рассмотреного случая 1 (рис. 8.44)  равен
равен

Тогда



Рисунок 8.44 – К вычислению интеграла Мора
Как видно, решения по теореме Кастильяно и с использованием интеграла Мора совпадают.
8.9.5.4. Графоаналитический способ Верещагина
Вычисление интеграла Мора по определению перемещений можно проводить по графоаналитическому способу Верещагина. По этому способу перемещение в направлении приложенной единичной силы определяется по формуле:

где 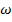 – площадь эпюры изгибающих моментов М от заданной нагрузки для балки;
– площадь эпюры изгибающих моментов М от заданной нагрузки для балки;  – ордината эпюры изгибающих моментов от единичной нагрузки под центром тяжести площади
– ордината эпюры изгибающих моментов от единичной нагрузки под центром тяжести площади 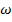 .
.
В применении способа Верещагина необходимо учитывать следующее:
а) эпюры изгибающих моментов должны быть разбиты на такие участки, в пределах каждого из которых хотя бы одна из эпюр была линейной;
б) при перемножении эпюр ставим знак минус, если эпюры находятся по разные стороны от оси отсчета.
Для практического вычисления перемещений по способу Верещегина необходимо:
1) построить эпюру изгибающих моментов от заданной нагрузки (основная эпюра);
2) снять с балки заданную нагрузку и приложить в сечении, перемещение которого ищется в направлении этого перемещения, единичную силу, когда ищется прогиб, или единичный момент, если искомым является угол поворота сечения;
3) построить эпюру изгибающих моментов от единичной нагрузки (единичная эпюра);
4) разбить эпюры от заданных нагрузок на отдельные площади  и вычислить ординаты
и вычислить ординаты  единичной эпюры под центром тяжести этих площадей.
единичной эпюры под центром тяжести этих площадей.
5) составить произведение  и просуммировать их.
и просуммировать их.
Рассмотрим типичные случаи нагрузки балки.
Таблица 8.2 – Площади эпюр и положения их центров тяжести
| Вид эпюры изгибающего момента | Величина площади 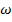 | Координата центра тяжести хц.т. | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 |  |  |
Случай3. Определить прогиб балки в т.В под силой Р (рис.8.45, а).
Решение
Площадь эпюры М от силы Р равна:  (рис.8.45, б).
(рис.8.45, б).
Ординату  эпюры М от действия на балку единичной силы
эпюры М от действия на балку единичной силы  (рис.8.35, в) находим из подобия треугольников (рис.8.35, г):
(рис.8.35, в) находим из подобия треугольников (рис.8.35, г):


Рисунок 8.45 – К вычислению прогиба балки в т. В по способу Верещагина
В итоге по формуле (8.62) находим прогиб балки на конце консоли в т.В, где приложена сосредоточенная сила Р:

Полученный результат совпадает с предыдущими решениями с использованием теоремы Кастильяно и интеграла Мора.
Случай 4.Определить прогиб балки в т.С под силой Р (рис.8.36, а).
Эпюра моментов балки (рис. 8.36, б) под заданной нагрузкой состоит из двух треугольников, площади которых равны:



Рисунок 8.46 – К вычислению прогиба балки в т. С
Решение
Для балки под единичной силой  (рис.8.36, в) на эпюре М ординаты под центром тяжести площадей основной эпюры равны:
(рис.8.36, в) на эпюре М ординаты под центром тяжести площадей основной эпюры равны:
 .
.
Прогиб под силой Р в т.С по формуле (8.62) будет:


Случай 5. Определить угол поворота сечения балки а т.С, где приложен внешний момент 𝔐(рис. 8.47, а).
Решение
 Как и в предыдущем случае, основная эпюра изгибающих моментов для балки (рис.8.37, б) состоит из двух площадей:
Как и в предыдущем случае, основная эпюра изгибающих моментов для балки (рис.8.37, б) состоит из двух площадей:


| Рисунок 8.47 – К вычислению угла поворота балки в т. С |
 в т.С (рис.8.37, в), ординаты единичной эпюры М под центрами тяжести площадей основной эпюры М равны:
в т.С (рис.8.37, в), ординаты единичной эпюры М под центрами тяжести площадей основной эпюры М равны: 
Тогда угол поворота сечения балки в т.С от действия момента 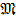 будет равен на основании формулы (8.62):
будет равен на основании формулы (8.62):


8.9.6 Решение типовых задач по определению перемещений балки энергетическими методами. Задания для индивидуальной работы
Пример 8.9.1. Введение дополнительной нагрузки. Для балки на рис.8.48, жестко заделанной одним концом и загруженной на другом конце сосредоточенной силой Р, определить угол поворота консоли в т.В по теореме Кастильяно.

 |
Решение
Непосредственно применить теорему Кастильяно к определению угла поворота конца консоли нельзя, т.к. в этом сечении нет обобщенной силы в виде внешнего момента. Поэтому вводится в этом сечении мысленный дополнительный момент  (см. рис. 8.48), направленный произвольно, который в окончательных расчетах следует положить равным нулю.
(см. рис. 8.48), направленный произвольно, который в окончательных расчетах следует положить равным нулю.
По теореме Кастильяно прогиб сечения балки в т.В по формуле (8.59)будет равен:

Выражение для изгибающего момента в сечении х (его удобно отсчитывать от конца консоли) описывается зависимостью  Пределы интегрирования при отсчете х от конца консоли будут 0 и l. Тогда угол поворота конца консоли соответствует выражению:
Пределы интегрирования при отсчете х от конца консоли будут 0 и l. Тогда угол поворота конца консоли соответствует выражению:

А так как дополнительную нагрузку  мы ввели мысленно и ее на самом деле нет, то под знаком интеграла ее следует положить равной нулю (
мы ввели мысленно и ее на самом деле нет, то под знаком интеграла ее следует положить равной нулю (  ):
):

Знак минус свидетельствует о принятом правиле знаков для перемещений: сечение конца консоли от силы Р поворачивается почасовой стрелке.
Пример 8.9.2. Наличие нескольких участков внешней нагрузки. Для балки на рис.8.49 найти угол поворота сечения С по теореме Кастильяно.

Рисунок 8.49 – К определению угла поворота сечения балки по теореме Кастильяно
Решение
В т.С балки приложен внешний момент 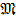 , поэтому в этом сечении можно найти угол поворота согласно условиям применения теоремы Кастильяно.
, поэтому в этом сечении можно найти угол поворота согласно условиям применения теоремы Кастильяно.
Точка приложения момента 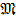 делит балку на два участка ВС и АС. Поэтому угол поворота сечения в т. С определим по этим двум участкам:
делит балку на два участка ВС и АС. Поэтому угол поворота сечения в т. С определим по этим двум участкам:

где 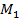 и
и  – изгибающие моменты в сечении т. С соответственно первого и второго участков.
– изгибающие моменты в сечении т. С соответственно первого и второго участков.
Пределы интегрирования по участкам целесообразно указывать тогда, когда будет решено, от каких точек по длине балки удобно отсчитывать координату х сечений по участкам.
Для первого участка ВС координату 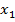 удобно отсчитывать от конца консоли т.В, так как в выражение для изгибающего момента в этом сечении не войдут другие силовые факторы для балки (внешний момент
удобно отсчитывать от конца консоли т.В, так как в выражение для изгибающего момента в этом сечении не войдут другие силовые факторы для балки (внешний момент 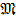 , реакции заделки в т.А).
, реакции заделки в т.А).
Тогда

Отсюда первый интеграл в выражении для  будет равен нулю.
будет равен нулю.
При установлении изгибающего момента на втором участке АС координату 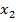 удобно отсчитывать от т.С (
удобно отсчитывать от т.С (  ), чтобы нижний предел второго интеграла был равен нулю. Тогда изгибающий момент на втором участке будет (отбрасываем мысленно правую от сечения часть балки):
), чтобы нижний предел второго интеграла был равен нулю. Тогда изгибающий момент на втором участке будет (отбрасываем мысленно правую от сечения часть балки):

Определившись с пределами интегрирования на втором участке, получаем:


Таким образом, искомый угол поворота сечения балки в т.С является суммой двух факторов: первого, вызванного силой Р и направленного по часовой стрелке (угол отрицателен) и второго – от момента 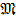 при угле поворота сечения против часовой стрелки (угол положителен).
при угле поворота сечения против часовой стрелки (угол положителен).
