Классификация функций одного аргумента
Принята следующая классификация:
- Целая рациональная функция или многочлен
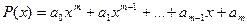
Над аргументом выполняются действия: сложение, вычитание, умножение, возведение в целую положительную степень.
- Дробно-рациональная функция
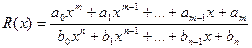
1) и 2) – класс рациональных функций.
- Иррациональная функция
Над аргументом х помимо вышеперечисленных операций производится операция извлечения корня конечное число паз и при этом результат не является рациональной функцией.
Пример 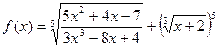
Совокупность рациональных и иррациональных функций образует класс явных алгебраических функций
- Многозначная неявная функция
Это - более общий случай алгебраических функций
 , где n – целое положительное число
, где n – целое положительное число
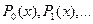 - целые рациональные функции от х.
- целые рациональные функции от х.
Пример 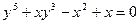
- Трансцендентные функции
Всякая неалгебраическая функция называется трансцендентной.
Элементарные трансцендентные функции:
a) показательная 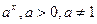 ;
;
b) логарифмическая функция  ;
;
c) тригонометрические функции sinx, cosx, tgx, ctgx;
d) обратные тригонометрические функции arcsinx, arccosx, arctgx, arcctgx.
Предел функции
В математическом анализе, как правило, рассматриваются безразмерные величины, то есть величины, лишенные физического содержания. Совокупность значений таких величин представляют собой некоторые числовые множества.
Формализуем определение функции.
Определение 1
Пусть X и Y – данные числовые множества. Если в силу некоторого соответствия f, сопоставляющего элементам множества X элементы множества Y,  (единственный), то y называется функцией от х, определенной на множестве Y.
(единственный), то y называется функцией от х, определенной на множестве Y.
Обозначение y=f(x)  (1)
(1)
Множество значений функции (1), по смыслу определения, содержится в Y, то есть 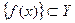 . Можно сказать, что функция f отображает множество X в множество Y.
. Можно сказать, что функция f отображает множество X в множество Y.
Графическая интерпретация.

Пример f(x)=sinx 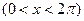 отображает интервал на отрезок [-1,1].
отображает интервал на отрезок [-1,1].
Пусть между элементами множеств X и Y функция y=f(x) устанавливает взаимнооднозначное соответствие, то есть 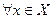 существует один и только один его образ
существует один и только один его образ 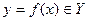 и обратно,
и обратно,  найдется единственный прообраз
найдется единственный прообраз 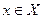 такой, что f(x)=y. Тогда функция
такой, что f(x)=y. Тогда функция 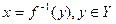 , устанавливающая соответствие между элементами множеств Y и X называется обратной для функции y=f(x). Иными словами обратная функция
, устанавливающая соответствие между элементами множеств Y и X называется обратной для функции y=f(x). Иными словами обратная функция 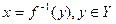 является отображением множества Y на множество X.
является отображением множества Y на множество X.
y=f(x) и 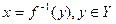 - взаимно обратные.
- взаимно обратные.
Определение 2
Под окрестностью  точки а (а – действительное число) будем понимать любой интервал
точки а (а – действительное число) будем понимать любой интервал 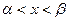 , окружающий эту точку
, окружающий эту точку  , из которого удалена точка а.
, из которого удалена точка а.

Под окрестностью 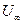 символа
символа  понимается внешняя часть любого отрезка
понимается внешняя часть любого отрезка  , то есть
, то есть 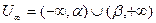
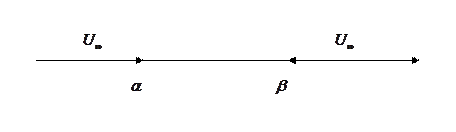
Для положительного числа  окрестность
окрестность  некоторой конечной точки а назовем ее
некоторой конечной точки а назовем ее  - окрестностью, если
- окрестностью, если 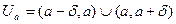 , то есть, если
, то есть, если 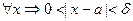

Пусть функция f(x) задана на множестве X. Точка а называется предельной точкой (точкой накопления) этого множества, если в любой ее  - окрестности содержится бесконечно много элементов
- окрестности содержится бесконечно много элементов 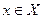 , то есть
, то есть  .
.
Определение 3
Число А называется пределом функции f(x) при 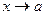 , то есть
, то есть 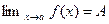 , если
, если 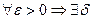 - окрестность
- окрестность  , что |f(x)-A|<
, что |f(x)-A|< 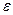 при
при 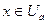 (2)
(2)
Неравенство (2) должно выполняться для всех тех х, для которых определена функция f(x), то есть для 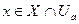 ; согласно определению предельной точки в каждой окрестности
; согласно определению предельной точки в каждой окрестности  множество таких точек не пусто.
множество таких точек не пусто.
Замечание 1
По смыслу определения предела функции, числа  можно полагать достаточно малыми.
можно полагать достаточно малыми.
Определение 4
Утверждение 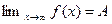 (3) эквивалентно следующему |f(x)-A|<
(3) эквивалентно следующему |f(x)-A|< 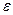 при
при  .
.
Множество всех точек х, для которых  , очевидно, является симметричной окрестностью
, очевидно, является симметричной окрестностью 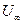 символа
символа  ; при этом предполагается, что для любой точки окрестности
; при этом предполагается, что для любой точки окрестности  , условно можно сказать, что
, условно можно сказать, что 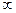 - есть предел множества Х – области определения функции f(x).
- есть предел множества Х – области определения функции f(x).
Объединяя определения 3 и 4 получим общее определение предела функции при 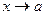 , которое справедливо как для конечного значения а, так и для
, которое справедливо как для конечного значения а, так и для 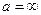 .
.
Общее определение предела функции
Пусть f(x) – функция, определенная на множестве X, и а – предельная точка этого множества. Число А является пределом функции f(x) при 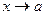 тогда и только тогда, когда
тогда и только тогда, когда 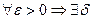 - окрестность
- окрестность 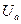 , что |f(x)-A|<
, что |f(x)-A|< 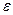 при
при 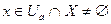 (4).
(4).
Короткая запись 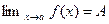 (5) или
(5) или 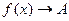 при
при 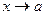 (5’).
(5’).
Теорема 1
Если функция f(x)=c постоянна в некоторой окрестности точки а, то  , причем с является единственным пределом этой функции при
, причем с является единственным пределом этой функции при 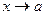 .
.
Определение 5
Функция f(x) называется ограниченной на данном множестве Х, если существует такое положительное число М, что  при
при 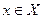 (6). Если такого числа М нет, то функция f(x) называется неограниченной.
(6). Если такого числа М нет, то функция f(x) называется неограниченной.
Лемма
Функция f(x), имеющая предел А при 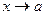 , ограничена в некоторой окрестности точки а.
, ограничена в некоторой окрестности точки а.
Доказательство
Пусть  при
при 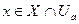 , где
, где 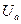 - соответствующая окрестность точки а. Отсюда для всех допустимых значений аргумента х получаем
- соответствующая окрестность точки а. Отсюда для всех допустимых значений аргумента х получаем
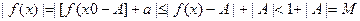 , если только
, если только 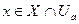 .
.
Отметим еще одну теорему, устанавливающую связь между границами функции и ее пределом.
Теорема 2
Пусть существует 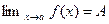 и M<f(x)<N (7) в некоторой окрестности
и M<f(x)<N (7) в некоторой окрестности 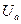 точки а. Тогда
точки а. Тогда  (8)
(8)
Доказательство
Пусть A<M. Полагая 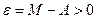 , в некоторой окрестности
, в некоторой окрестности 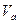 будем иметь
будем иметь
|f(x)-A|<M-A, то есть –(M-A)<f(x)<M-A. Отсюда, выбирая  , получаем, что f(x)<M, что противоречит левому неравенству (7). Аналогично опровергается предположение A>N. Таким образом, неравенство (8) доказано.
, получаем, что f(x)<M, что противоречит левому неравенству (7). Аналогично опровергается предположение A>N. Таким образом, неравенство (8) доказано.
Следствие
Положительная функция не может иметь отрицательного предела.
