Определители и системы линейных алгебраических уравнений

Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства:

1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.

2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.

3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.

4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число. Для определителей третьего порядка это свойство может быть записано, например, так:

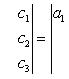
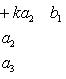
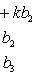
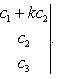
6. Определитель второго порядка вычисляется по формуле

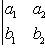
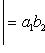
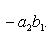(1)

7. Определитель третьего порядка вычисляется по формуле

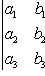
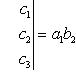
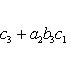
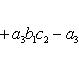
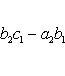
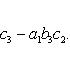(2)

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

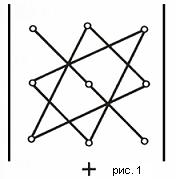
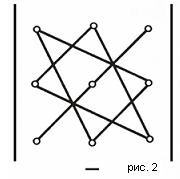
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений.

В определителе порядка n алгебраическим дополнением элемента, стоящего на пересечении k-го столбца и l-й строки, называется определитель порядка (n - 1), получаемый из данного вычеркиванием в нем строки и столбца, на пересечении которых стоит этот элемент, причем к этому определителю присоединяется множитель (-1)^k+l, где (k + l) - сумма номеров вычеркнутой строки и столбца. Алгебраическое дополнение элемента, рассматриваемое без множителя (-1)^k+l, называется минором этого элемента.

Пример. В определителе 5-го порядка

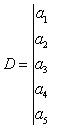
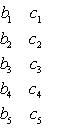
(3)

алгебраическим дополнением, соответствующим элементу d₃, будет определитель 4-го порядка

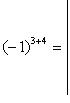
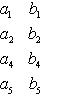
Здесь в показателе степени у (-1) три - номер строки, четыре - номер столбца, на пересечении которых стоит элемент d₃.

8. Определитель равен сумме произведений каждого элемента некоторой строки (или столбца) на его алгебраическое дополнение.

Условимся обозначать элементы определителя маленькими буквами, а их алгебраические дополнения - соответствующими большими буквами с теми же индексами. Так, как алгебраическое дополнение элемента a₃ будем обозначать через A₃, алгебраическое дополнение элемента d₄ - через D₄ и т. д. На основании свойства 8 определитель (3) может быть представлен, например, в таком виде:

D = a₃A₃ + b₃B₃ + c₃C₃ + d₃D₃ + e₃E₃.

Это равенство представляет собой разложение определителя по элементам третьей строки. По свойству 8 вычисление определителя порядка n сводится к вычислению определителей порядка (n - 1).

9. Если все элементы какого-нибудь ряда определителя, кроме одного, равны нулю, то определитель равен этому не равному нулю элементу, умноженному на его алгебраическое дополнение.

С помощью указанных свойств можно вычислить определитель любого порядка.