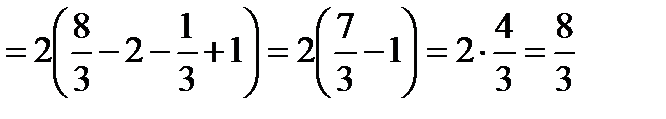Свойства функции. Исследование функции с помощью производной и построение графика функции.

Функция у = f (х) называется возрастающей на промежутке X, если для любых 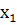и и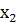з области определения, таких, что при 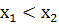выполняется неравенство .

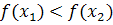Функция у = f (х) называется убывающей на промежутке X, если для любых 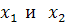из X, таких, что при 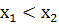выполняется неравенство .

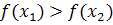Достаточное условие возрастания функции:

Если в каждой точке интервала (a, b) f'(x)>0, то функция f(x) возрастает на этом интервале.

Достаточное условие убывания функции:
Если в каждой точке интервала (a, b) f'(x)<0, то функция f(x) убывает на этом интервале.

Минимум и максимум функции.

Определение:

Точка 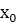называется точкой минимума функции f, если для всех x из некоторой окрестности 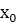выполняется неравенство f(x) ≥ f( ).

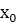Определение:

Точка 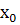называется точкой максимума функции f, если для всех x из некоторой окрестности 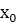выполняется неравенство f(x) ≤ f( ).

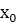Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.

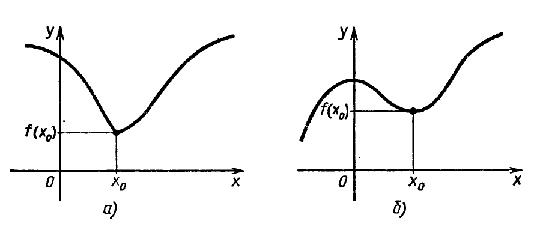
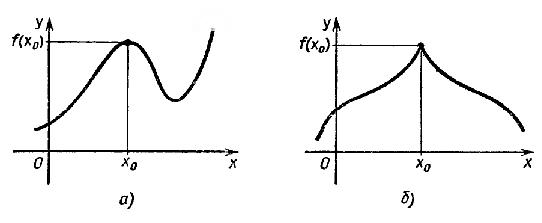
Достаточное условие экстремума

Если при переходе через точку 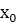производная функции меняет знак, то 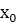–точка экстремума функции f(x).

Необходимое условие экстремума

Если x₀ - точка экстремума функции f ( x ), то f ’ ( x₀) = 0 или не существует.

Пример нахождения экстремума:

Найти экстремумы функции f ( x ) = 2x³ - 15x² + 36x - 14.

Решение.

Так как f `( x ) = 6x ² - 30x +36 = 6( x -2)( x - 3), то критические точки функции x = 2 и x = 3.

Экстремумы могут быть только в этих точках. Так как при переходе через точку x = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x = 3 производная меняет знак минус на плюс, поэтому в точке x = 3 у функции минимум.

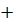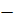2 3

min max

Вычислив значения функции в точках:

x = 2 и x = 3, найдем экстремумы функции:

максимум f(2)=14 и минимум f(3)=13.

Правило нахождение экстремума функции:

Найти производную f ‘(x)

Найти критические точки функции у = f(x),т.е. точки, в которых f’(x)=0 или терпит разрыв.

Исследовать знак производной f ‘(x) в промежутках, на которые критические точки делят область определения функции. x0 – точка минимума, если она отделяет промежуток, в котором f ‘(x)<0, от промежутка f ‘(x)>0, и точка максимума в противном случае. Если в соседних промежутках знак производной не меняется, то в этой точке функция экстремума не имеет.

Вычислить значения функции в точках экстремума.

Выпуклость, вогнутость и точки перегиба функции.

Eсли f '' ( x ) > 0 для любого x ( a, b ), то функция

f ( x ) является вогнутой на интервале ( a, b );

Eсли f '' ( x ) < 0 для любого x ( a, b ), то функция

f ( x ) является выпуклой на интервале ( a, b )

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.

Отсюда следует, что если в точке перегиба x₀ существует вторая производная f '' ( x₀ ), то f '' ( x₀ ) = 0.

Пример нахождения интервалов выпуклости и вогнутости функции.

Рассмотрим график функции y = x³ :

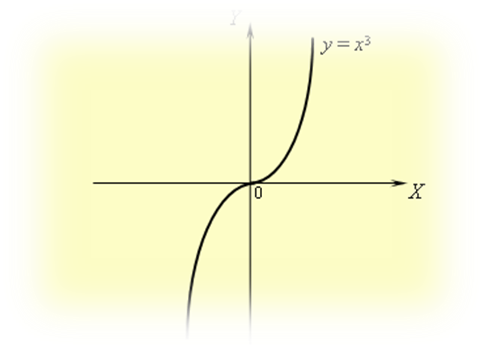
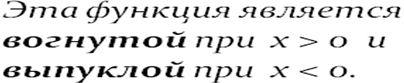
В самом деле, y'' = 6x, но 6x > 0 при x > 0 и

6x < 0 при x < 0, следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x³ является вогнутой при x > 0 и выпуклой при x < 0.

Тогда x = 0 является точкой перегиба функции y = x³.

Построение графиков функций.

Общая схема исследования графиков функций.

1. Найти область определения функции.

2. Выяснить, является функция четной или нечетной.

3. Найти точки пересечения графика с осями координат (если это не вызывает затруднение).

4. Найти асимптоты графика функции.

5. Найти промежутки монотонности функции и ее экстремумы.

6. Найти промежутки выпуклости графика функции и точки перегиба.

7. Построить график, используя полученные результаты исследования.

Пример: Построить график функции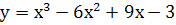

1. Функция определена на всей числовой прямой, т. е. ,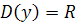

2. Данная функция не является ни четной ни нечетной.

3. Найдем точку пересечения графика функции с осью Оу: полагая х=0 получим у=-3, точки пересечения графика функции с осью Ох найти затруднительно.

4. График функции не имеет асимптот. ( )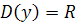

5. Найдем экстремумы данной функции: 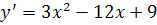. Далее имеем:

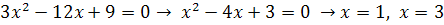. Исследуем производную на знак, в промежутках, на которые полученные точки делят облсать определения функции.

x	( 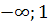)		(1;3)		(3; +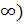
f ’(x)	+				+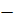
f(x)				-3

max min

y(1)=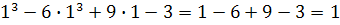

y(3)=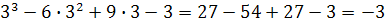

6. Найдем точки перегиба функции и промежутки выпуклости графика функции, для чего находим вторую производную:

У''=6х-12 6х-12=0 6х=12 х=2 – критическая точка

Исследуем вторую производную на знак, в промeжутках, на которые критическая точка, делит область определения функции.

х	( 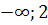)		(2; +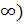
f’’(x)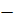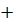
f(x)		-1
		перегиб

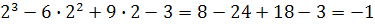Итак точка х=2 является точкой перегиба.

8.По полученным данным построим график.

Неопределённый интеграл:

Пример:

1. Найти неопределенный интеграл интеграл:

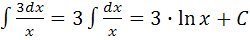
2.

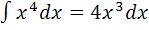
3.

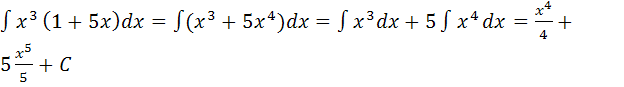
Основные формулы интегрирования. (табличные интегралы)

B AgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQI ECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAgQIECBA gAABAgQIECBAgAABAgQIECBAgAABAgQIECBAgAABAqMF/i/zZSq/LDuClwAAAABJRU5ErkJgglBL AQItABQABgAIAAAAIQBHPW7kCQEAABMCAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBl c10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAAOgEAAF9yZWxz Ly5yZWxzUEsBAi0AFAAGAAgAAAAhAOwFQwOLBAAAZhUAAA4AAAAAAAAAAAAAAAAAOQIAAGRycy9l Mm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAKomDr68AAAAIQEAABkAAAAAAAAAAAAAAAAA8AYAAGRy cy9fcmVscy9lMm9Eb2MueG1sLnJlbHNQSwECLQAUAAYACAAAACEAnHIL990AAAAFAQAADwAAAAAA AAAAAAAAAADjBwAAZHJzL2Rvd25yZXYueG1sUEsBAi0ACgAAAAAAAAAhANss1Bo4VAEAOFQBABQA AAAAAAAAAAAAAAAA7QgAAGRycy9tZWRpYS9pbWFnZTEucG5nUEsFBgAAAAAGAAYAfAEAAFddAQAA AA== ">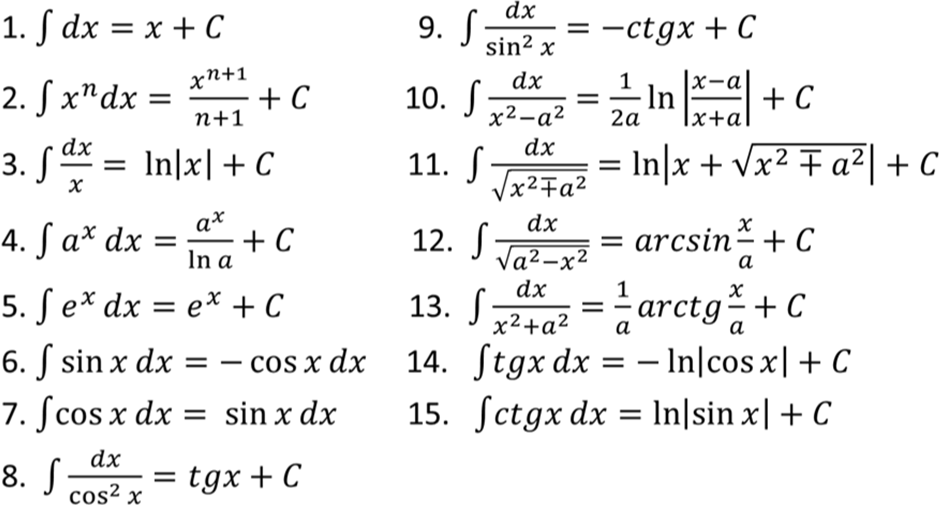

,

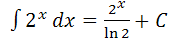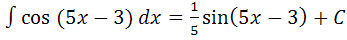
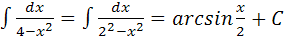
Примеры:

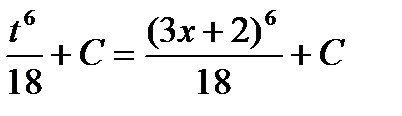
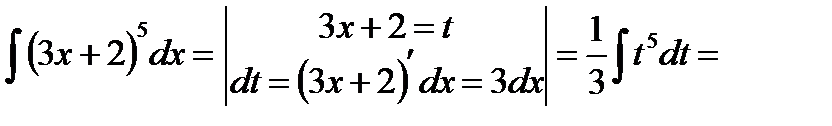Найти следующие интегралы:

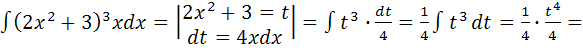
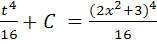
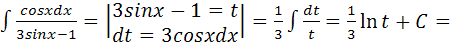
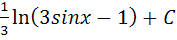
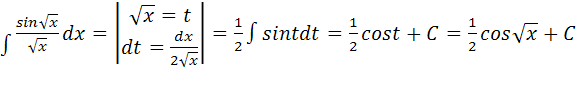
Определенный интеграл.

Определенный интеграл вычисляется по формуле Ньютона –Ленйбница. С геометрической точки зрения – определенный интеграл равен площади криволинейной трапеции.

y=f(x)

X

Свойства определенного интеграла:

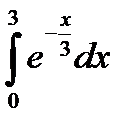Вычисление определенного интеграла. Формулу Ньютона-Лейбница.Пример:

Вычислить определенный интеграл:

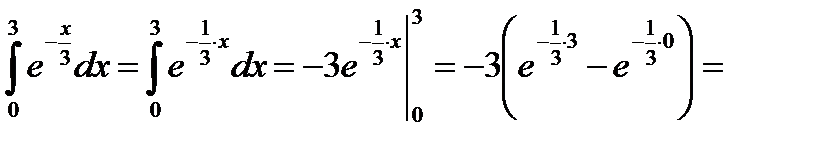
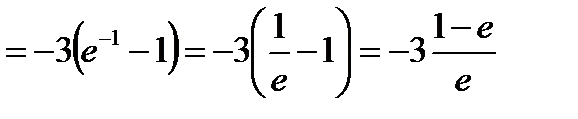
Метод замены переменной в определенном интеграле.

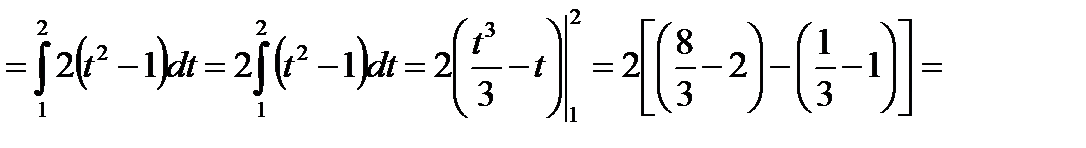
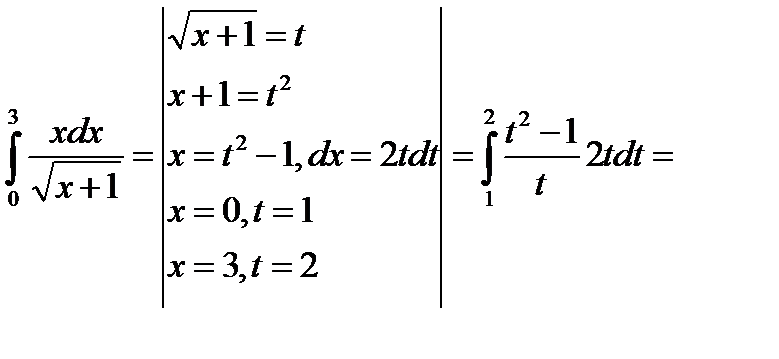Пример: