Egrave; Из общего решения /общего интеграла ДУ-1 частное решение ДУ выделяется выбором соответствующего значения константы С.

Методическая Литература по курсу.

1. Бугров Я.С., Никольский С.М., Высшая математика. Т.3. Учебник для ВУЗов.
- М.: Наука, 2003, 2004.

2. Сборник задач по математике для втузов.ч.3./Под ред. А.В. Ефимова, А.С. Поспелова.

-4-е изд. – М.:Физматлит, 2003, 2007.

3. Бодунов Н.А., Пилюгин С.Ю. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Учебное пособие, СПбГЭТУ, СПб, 2011

4. Е.З. Боревич, Е.Е. Жукова, А.Л. Меркулов. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. Методические указания. СПбГЭТУ, СПб, 2003

3. С.А. Колбина, Г.К. Коновалов О.А. Снетков, Типовые расчеты по дисциплине
«Математический анализ», Учебное пособие, СПбГЭТУб С-Пб, 2008

4. Н.А. Каразеева, В.Л. Трегуб, Е.В. Фролова, Операционное исчисление, Учебное пособие, СПбГЭТУ,1998

Из «прошлого»…

Уравнение (УР): указать «область определения УР»; определить «решение УР»; «решить УР»

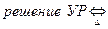- подстановка обращает УР в верное числовое равенство.

- «решить УР» 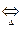найти множество его решений (ВСЕ решения!)

[I]Числовое УР(алгебраическое, показательное, логарифмическое и т.п.)

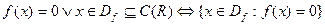
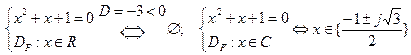
[II]Функциональное УР (неявное задание функции):

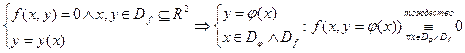
- решение ФУРó функция, обращающая ФУР в области допустимых значений в тождество.
è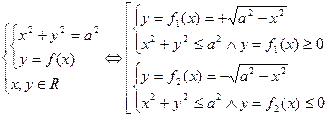

Экзаменационные задачи к главе «ОДУ».

1. Доказать, что f(x)= xe^x- решение ОДУ-2 : y^//+2xy^/+y =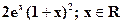

2) Являются ли решениями ДУЧП-2 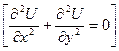функции U(x,y,a)=x³+axy² ?

3. Для ДУ 2 порядка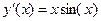

1) Найти общее решение; 2) Найти решение задачи Коши с нач. усл. y(π/2)=1

4. Для ДУ у'=(1-x²)y² найти решения з. Коши с нач условиями y(-1)=1 и y(1)=1

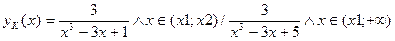
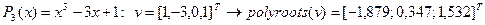
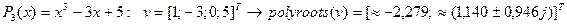
5. Доказать, чтоДУ-1 dy=f(y/x) приводится к ДУРП подстановкой z(x)=y(x)/x и решить
ДУ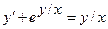

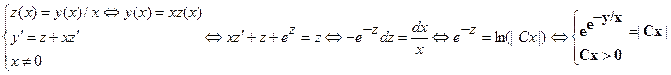
6.Решить ДУ y’+2y=y²exp(x) и найти решение з.Коши: y(0)=1

óДУ Бернулли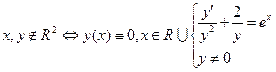

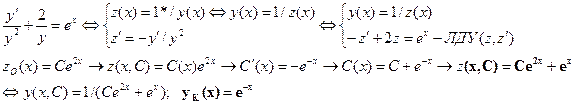
7.Указать тип ДУ-1: ДУРП, ОЛДУ(?,?), НЛДУ(?, ?), ДУБ(n = ?)

1) (x-2xy-y²)dy+y²dx=0 --- НЛДУ( x(y),dx)

2) (y²x’+(1-2y²)x=0; --- ОЛДУ( x(y),x’)

3) x²dy+(3-2xy)dx=0; --- НЛДУ(y(x),dy)

4) (3y²+1)y’-2x=0 --- ДУРП

5) 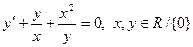--- ДУБ n=- 1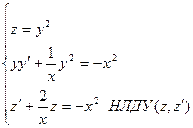

8.Решить задачу Коши: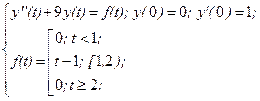

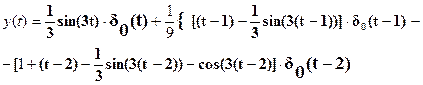
§1 Дифференциальные уравнения : основные понятия.

Определение 1.1 Дифференциальным уравнением порядка “n” (ДУ-n) называют уравнение 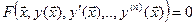, связывающее аргумент 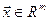, функцию 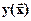и ее производные функции y⁽ⁱ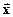⁾( ), i=1,..,n, порядок старшей из которых равен “n”,

при этом ДУ относительно функции одной переменной (n=1) называют «обыкновенным ДУ (ОДУ)», а ДУ относительно функции нескольких переменных (n≥2) и ее частных производных называют «ДУ в частных производных (ДУЧП)» .

è В ДУ-n в явном виде должна входить производная функция порядка n!

èy^//+2y^/=e^x ; y”=1– ОДУ-2.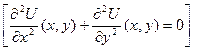 - ДУЧП-2.

Определение 2.1n раз дифференцируемая функция 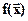называется решением ДУ-n в областиопределения, если подстановка этой функции обращает ДУ в тождество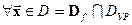

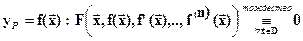
è Например,

(1) функция 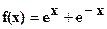является решением ОДУ-2 y^// + y^/ = 2e^x 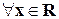,так как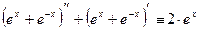

(2) Множество функций { 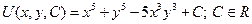} образуют множество решенийДУЧП-1

.

------------------------------------------------------------------------

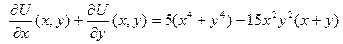ЭКЗ-1: 1)Доказать, что f(x)= xe^x- решение ОДУ-2 : y^//+2xy^/+y =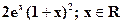

2) Является ли решением ДУЧП-2 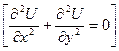функция U(x,y)=x³+axy² ?

-----------------------------------------------------------------

Дифференциальное уравнение 1 порядка: частное и общее решения ДУ; общий интеграл ДУ ; решение задачи Коши.

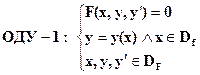(1)

ОПРЕДЕЛЕНИЯ.

1.Дифференцируемая функция y=φ(x): 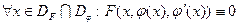называется
частным решением ДУ

Гладкая линия 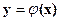- график решения ДУ на координатной плоскости ХОУ,

называетсяинтегральной кривой ДУ.

2.Функцияφ(x,C),содержащая произвольную константу, называется общим решением ДУ-1,

если при любом допустимом значении константы она является решением ДУ.

Уравнение 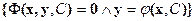, содержащее произвольную константу и определяющее неявно общее решение ДУ, называется общим интегралом ДУ-1.

egrave; Из общего решения /общего интеграла ДУ-1 частное решение ДУ выделяется выбором соответствующего значения константы С.

3. Частное решениеДУ-1, удовлетворяющее условию y(x₀)=y₀,

называется решением задачи Коши с заданным начальным условием:

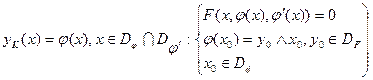
èИнтегральная криваяy=y_K(x)проходит через точку М₀(х₀,у₀) на ХОУ.

èФункция y_K(x)=φ(x)является решением задачи Кошина интервале 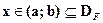, если
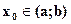- и φ(x)дифференцируема на интервале ( ).

-----------------------------------------------------------------------------------------------------------------

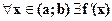ПРИМЕРЫ.

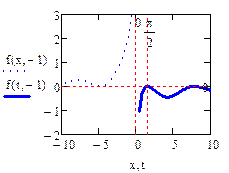
(1) xy’+y=cos(x); D_F: !!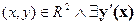

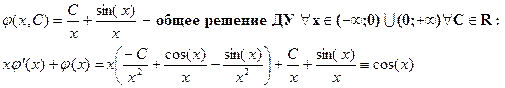
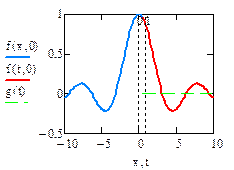
Найдём решение з. Коши с начальным условием x₀=1, y₀= y(1)=sin(1)

è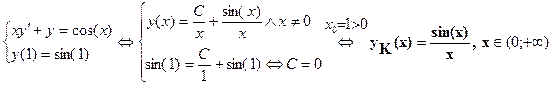

èУбедитесь в том, что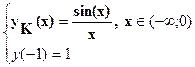

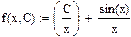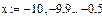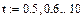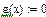ЭКЗ-2.Найти решение задачи Коши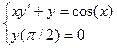

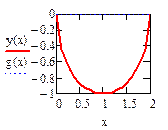
(2)Доказать/проверить, что уравнение 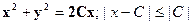является общим интегралом ДУ-1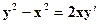
è Для доказательства продифференцируем уравнение и исключим константу из системы двух уравнений:

è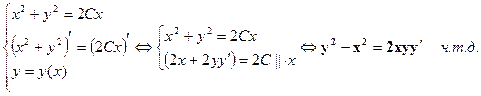
è Выделим из общего интеграла решение задачи Коши с условием x₀=1, y₀=-1 :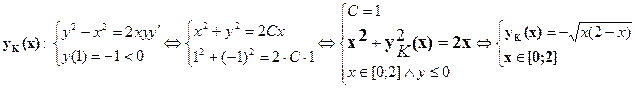

---------------------------------------------------------------------------------------------------

§3 Теорема существования и единственности решения задачи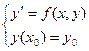

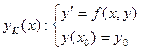
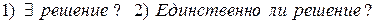
Для ДУ-1 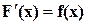ответы на эти вопросы известныизДИФОП и ИИФОП.

1) Решение ДУ существует в области 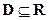непрерывности функции f(x) и называется первообразной функции f(x).

2) Существует бесконечное множество первообразных, называемое «неопределенным интегралом» 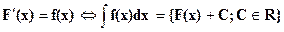èИнтегральные кривые ДУ y=F(x) представляют семейство параллельных гладких линий.

3) Задача Коши с начальным условием F(x₀)=y₀ 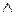(x₀,y₀) 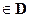имеет единственное решение – через любую точку области на плоскости XOYпроходит единственная интегральная кривая ДУ.

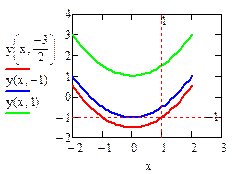Например, y/(x)=x ó{y(x,C)=x²/2+C; 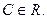Общее решение ДУ-1è решение з. Коши:

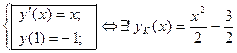
ЭКЗ-2Для ДУ-1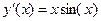

1) Найти общее решение; 2) Найти решение задачи Коши с нач. усл. y(π/2)=1

Для ДУ-1 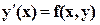имеет место следующее

Утверждение. (Теорема существования и единственности решения з. Коши)

Если функция f(x,y)непрерывна в области 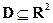и имеет в этой области ограниченную частную производную по y ( 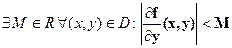), то через любую точку области 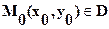проходит единственная интегральная кривая 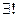y=y_K(x): .

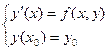Примеры.
(1) ДУ y'(x)= f(x,y)=(1-x²)y² определено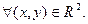

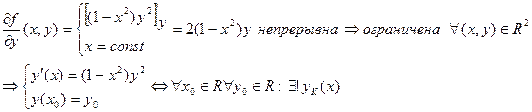
(2) xy’+y=cos(x)(см. §2)è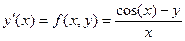
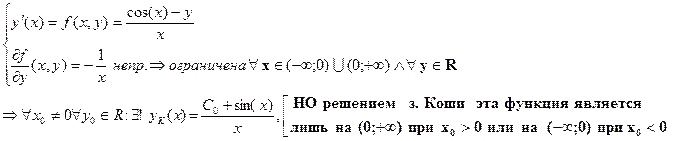
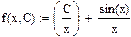
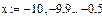
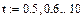