Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключение неизвестных (методом Гаусса)

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров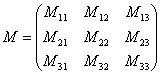

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

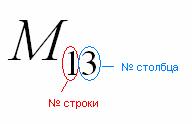
То есть, двойной подстрочный индекс указывает, что элемент 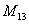находится в первой строке, третьем столбце, а, например, элемент 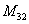находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

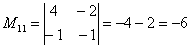
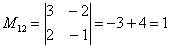
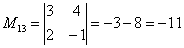
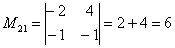
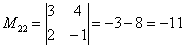
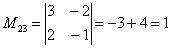
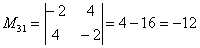
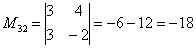
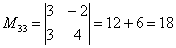
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).

Таким образом:

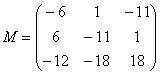– матрица миноров соответствующих элементов матрицы .

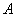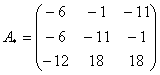– матрица алгебраических дополнений.

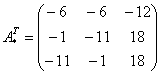– транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?

Теперь записываем обратную матрицу:

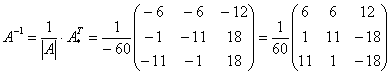
Ни в коем случае не вносим 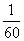в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение. Умножать матрицы можно научиться на урокеДействия с матрицами. Кстати, там разобран точно такой же пример.

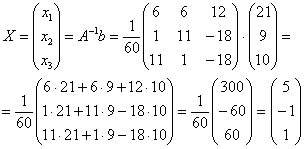
Обратите внимание, что деление на 60 выполняется в последнюю очередь.
Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.

Ответ: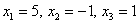

Пример 12

Решить систему с помощью обратной матрицы.

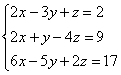
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса). Доступно объяснить алгоритм не так-то просто, но я старался!.

Желаю успехов!

Ответы:

Пример 3: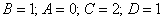

Пример 6: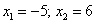

Пример 8: 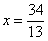, 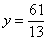. Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).

Примеры 10, 12: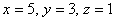

7) Как решить систему линейных уравнений?

На данном уроке мы рассмотрим методы решения системы линейных уравнений. В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, например, «Решить систему по формулам Крамера», так и в ходе решения остальных задач. С системами линейных уравнений приходиться иметь дело практически во всех разделах высшей математики.

Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: 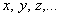без всяких причудливых вещей вроде 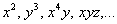и т.п., от которых в восторге бывают только участники математических олимпиад.

В высшей математике для обозначения переменных используются не только знакомые с детства буквы .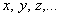
Довольно популярный вариант – переменные с индексами: .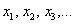
Либо начальные буквы латинского алфавита, маленькие и большие: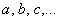
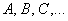
Не так уж редко можно встретить греческие буквы: 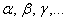– известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю»: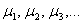

Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения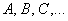

Но как бы ни обозначались переменные, принципы, методы и способы решения системы линейных уравнений от этого не меняются. Таким образом, если Вам встретится что-нибудь страшное типа 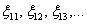, не спешите в страхе закрывать задачник, в конце-концов, вместо 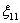можно нарисовать солнце, вместо 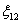– птичку, а вместо 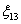– рожицу (преподавателя). И, как ни смешно, систему линейных уравнений с данными обозначениями тоже можно решить.

Что-то у меня есть такое предчувствие, что статья получится довольно длинной, поэтому небольшое оглавление. Итак, последовательный «разбор полётов» будет таким::

Решение системы линейных уравнений методом подстановки («школьный метод»). – Решение системы методом почленного сложения (вычитания) уравнений системы. – Решение системы по формулам Крамера. – Решение системы с помощью обратной матрицы. – Решение системы методом Гаусса.

С системами линейных уравнений все знакомы из школьного курса математики. По сути дела, начинаем с повторения.