В недесяткових системах числення 8 страница
1) Місткість однієї банки 3л. Скільки потрібно банок, щоб розлити 6л фруктового соку? 9л? 12л? 15л?
2) За перший день магазин продав 8 однакових портфелів і отримав за них 32 грн. За другий день було продано 6 таких портфелів. Скільки грошей отримали за портфелі на другий день?
3) Із 24 кг молока виходить 3кг сливок, із 20кг сливок одержують 4кг масла, а із 12кг масла одержують 9кг топленого масла. Скільки кілограмів топленого масла можна отримати із 2400кг молока?
4. Сторони прямокутника 6см і хсм. Площа цього прямокутника усм2. Запишіть формулу, яка виражає залежність площі цього прямокутника від довжини сторони. Побудуйте графік цієї залежності при умові, що х 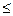 8.
8.
5. Маса одного олівця дорівнює 1,5г. Позначте масу х олівців через у (в г) і побудуйте графік одержаної залежності при умові, що х 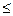 4.
4.
Обернена пропорційність
Якщо s км – відстань, яку треба пройти туристу, t ч – час руху, а v – км/год – його швидкість
То кожному значенню швидкості співпадає єдине значення часу. Формула 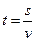 задає функцію. Її називають оберненою пропорційністю.
задає функцію. Її називають оберненою пропорційністю.
Оберненою пропорційністю називається функція, яку можна задати за допомогою формули виду 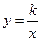 , де х – незалежна змінна, а k – не рівне нулю число.
, де х – незалежна змінна, а k – не рівне нулю число.
Про змінну у говорять, що вона обернено пропорційна змінній х.
Областю визначення функції 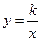 є множина дійсних чисел, відмінних від нуля.
є множина дійсних чисел, відмінних від нуля.
Графіком оберненої пропорційності є гіпербола.
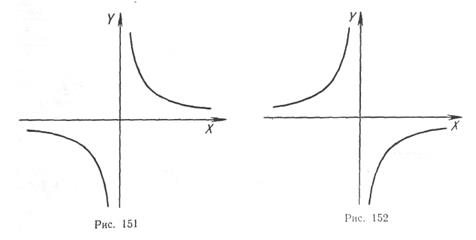
При k>0 її вітки знаходяться в першій і третій четвертях (мал. 151) при k<0 – в другій і четвертій (мал. 152). Щоб побудувати гіперболу, потрібно скласти таблицю значень функції 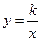 . Так, для функції
. Так, для функції 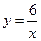 , де х – дійсне число, відмінне від нуля, таблиця значень може бути такою:
, де х – дійсне число, відмінне від нуля, таблиця значень може бути такою:
| х | |||||
| у | 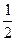 |
 |
При від’ємних значеннях х графік функції будується симетрично відносно початку координат. Якщо функція f – обернена пропорційність і (х1, у1), (х2, у2) – пари відповідних значень х і у, при чому х2 ≠0, у1≠0, то 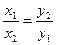 . Іншими словами, якщо
. Іншими словами, якщо 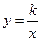 , то відношення двох значень змінної х рівне оберненому відношенню відповідних значень у.
, то відношення двох значень змінної х рівне оберненому відношенню відповідних значень у.
Дійсно, якщо f – обернена пропорційність, то вона може бути задана формулою 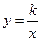 , і тоді для двох різних значень х1 і х2 маємо, що
, і тоді для двох різних значень х1 і х2 маємо, що 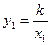 ,
, 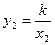 . Так як х2≠0 і k≠0, у1≠0, то
. Так як х2≠0 і k≠0, у1≠0, то 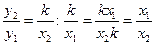 . Тому
. Тому 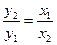 .
.
Якщо значеннями змінних х і у є додатні числа, то доведене можна сформулювати так:
Із збільшенням (зменшенням) значень змінної х в декілька раз відповідне значення змінної у зменшиться (збільшиться) в стільки ж раз.
Наведемо приклади таких задач.
1. Потрібно спакувати в пакети 24 кг муки. Яка буде маса 1 пакета, якщо цю муку спакувати в 3 однакових пакети? в 4 пакети? в 6 пакетів? в 8 пакетів?
В задачі розглядаються три величини: маса всієї муки, кількість пакетів і маса муки в одному пакеті. Перша величина приймає одне і теж значення 24 Дві інші знаходяться в обернено пропорційній залежності, так як цю залежність можна виразити формулою 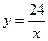 , де х – кількість пакетів, а у – маса муки в одному пакеті. Знаючи це, легко знайти, що якщо муку спакувати в 3 пакета, то в одному пакеті буде 24:3=8(кг) муки; якщо в 4 пакета, то в одному пакеті буде 24:4=6(кг) муки і т.д.
, де х – кількість пакетів, а у – маса муки в одному пакеті. Знаючи це, легко знайти, що якщо муку спакувати в 3 пакета, то в одному пакеті буде 24:3=8(кг) муки; якщо в 4 пакета, то в одному пакеті буде 24:4=6(кг) муки і т.д.
2) З ділянки зібрали 4 мішки картоплі, по 50кг в кожному. Цю картоплю розклали для зберігання в ящики, по 20кг в кожний. Скільки ящиків потрібно?
В задачі розглядається залежність між всією масою картоплі між всією масою картоплі, масою картоплі в деякій ємності і кількість цих ємностей. Перша величина постійна, її значення знаходиться множенням: 5·4=200(кг), а дві інші знаходяться в обернено пропорційній залежності, яка може бути задана формулою 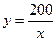 , де х – маса однієї ємності, у – кількість цих ємностей.
, де х – маса однієї ємності, у – кількість цих ємностей.
Вправи
1. Вкажіть серед наступних функцій, заданих табличним способом обернені пропорційності:
1)
| х | |||||
| у | 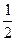 |
2)
| х | |||||
| у |
3)
| х | |||||
| у | -1 | -5 | -7 | -11 | -15 |
4)
| х | -2 | -4 | -3 | ||
| у | -2 | -1 |
2. Побудуйте графік функції 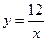 при умові, що її область визначення:
при умові, що її область визначення:
1) множина дійсних чисел;
2) 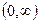 ;
;
3) 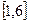 ;
;
4) 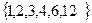 .
.
3. З’ясуйте, яка залежність існує між величинами, даними в задачі, і розв’яжіть її:
1) З грядки зібрали 24кг помідорів. Скільки потрібно пакетів щоб спакувати ці помідори по 1кг в пакет? по 3кг? по 4кг? по 6кг? по 8кг? по bкг?
2) Велосипедист їхав зі швидкістю 12 км/год і був в дорозі 2 год. Скільки часу потрібно пішоходу, щоб пройти цю відстань зі швидкістю 4 км/год?
3) Два столяра відремонтували стільців порівну. Перший столяр працював 6 днів, ремонтуючи по 10 стільців в день, а інший працював 5 днів. По скільки стільців в день ремонтував другий столяр?
4. Площа прямокутника з основою х см дорівнює 8см2. Як висота у цього прямокутника? Покажіть, що залежність між основою і висотою прямокутника при постійній площі є функцією, і побудуйте її графік при умові, що основа прямокутника не перевищує 0,5см.
5. Завдання «Заповни пропуск так, щоб запис 24:3>24: … був правильним» студент заповнив так:
Щоб частка 24 і 3 була більше частки чисел 24 і невідомого числа … , потрібно щоб другий дільник був менше першого, наприклад 2.
Яка властивість і якої функції неявно використав студент.
Вправи
1. На складі було 400 т вугілля. Кожного дня із цього запасу витрачалося по 50 т. Запишіть формулу, яка виражає залежність кількості вугілля на складі (ут) від часу (х дн.), доведіть, що ця формула задає функцію. Вкажіть область визначення цієї функції.
2. Довжина окружності (С) з радіусом R підраховується по формулі 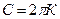 . Функціональну залежність між якими змінними задає ця формула? Яка область визначення даної функції?
. Функціональну залежність між якими змінними задає ця формула? Яка область визначення даної функції?
3. Чи знаходить площа квадрату в функціональній залежності від довжини його діагоналі?
4. Якому натуральному числу n із проміжку 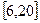 поставили в відповідності остача, яка виходить при діленні цього числа n на 4. Знайдіть його відношення за допомогою таблиці і обґрунтуйте, чого воно є функцією і яка його область визначення.
поставили в відповідності остача, яка виходить при діленні цього числа n на 4. Знайдіть його відношення за допомогою таблиці і обґрунтуйте, чого воно є функцією і яка його область визначення.
5. Знайдіть область визначення функції, задана формулою:
1) 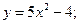
2) 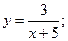
3) 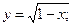
4) 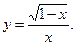
6. Наведіть приклади трьох вправ із посібників математики початкових класів, при виконанні яких можуть бути здійснена пропедевтика поняття функції.
7. Які із наступних вправ, взятих із підручників математики початкових класів, можуть бути використані для пропедевтики поняття функції і чого?:
1) Заповни таблицю:
| с | ||||
| 10·с |
2. Розв’яжи вираз 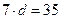 .
.
3) Збільш в 3 рази кожне із чисел: 7, 5, 9, 4, 8, 6.
4) Із ряду чисел 15, 16, 17, 18 випиши те значення с, при яких правильна нерівність 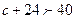 .
.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Боровик В. Н. Курс математики: Навч. посібник / - К. : Вища пік., 1995.- С. 272-293.
2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. -К. : Вища пік., 1987. - С. 143-151.
3. Стойлова Л. П. Основи начального курса математики. М.: Просвещение. 1988. - С. 262-277.
 Практичне заняття № 6
Практичне заняття № 6
Тема. Побудова графіків функцій та визначення їх властивостей.
Мета.Застосувати теоретичні відомості про функції, графіки і їх властивості та величини до розв’язування вправ.
Студенти повинні знати:
· визначення числової функції;
· способи задання функції;
· властивості функції;
· графіки основних видів функцій.
Студенти повинні вміти:
· будувати графіки функцій;
· визначати властивості функцій.
Література
1. Курс математики: Навч. посібник / В. Н. Боровик. – К. : Вища шк., 1995. С. 238 – 287. 349 – 379.
2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1980. С. 153-154, 157-161.
3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1987. С. 192 -199.
4. Основы начального курса математики: Учеб. пособие Л. П. Стойлова. - М. “Просвещение” 1988. С. 242 - 307.
План та хід заняття
І. Актуалізація опорних знань
1. Числові функції. Способи задання функцій.
2. Пряма і обернена пропорційність, їх властивості і графіки.
3. Лінійна функція і її графік.
ІІ. Розв’язування вправ
1. Відомо, що графік функції у=2х+b проходить через точку (1, 4). Чи пройде він через точку (3, 8)?
2. Знайти області визначення функцій:
1) 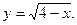 2)
2) 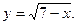 3)
3) 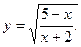 4)
4) 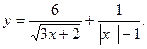 5)
5) 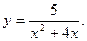
6) 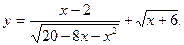 7)
7) 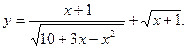 8)
8) 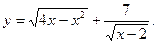
9) 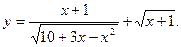 10)
10) 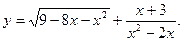
3. Знайти області значень функцій:
1) 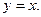 2)
2) 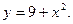
3) 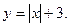 4)
4) 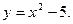
5) 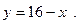 6)
6) 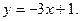
7) 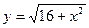 . 8)
. 8) 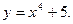
9) 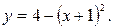 10)
10) 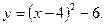
4. Визначити, парні чи непарні функції:
1) 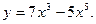 2)
2) 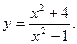 3)
3) 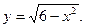
4) 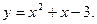 5)
5) 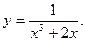 6)
6) 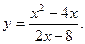
7) 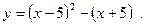 8)
8) 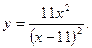 9)
9) 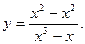
5. Дослідити на монотонність функції:
1) 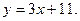 2)
2) 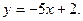 3)
3) 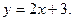 4)
4) 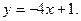
6. Доведіть, що функції f і g є взаємно оберненими:
1) 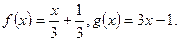 2)
2) 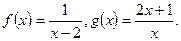
7. Знайдіть функцію, обернену до даної:
1) 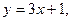 2)
2) 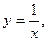 3)
3) 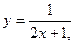 4)
4) 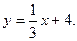 5)
5) 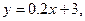 6)
6) 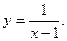
ІІІ. Самостійне розв’язування вправ
Варіант 1
1. Знайти область визначення функції: 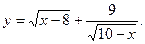
2. Знайти область значень функції: 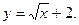
3. Визначити парна чи непарна функція: 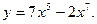
4. Визначити зростаюча чи спадна функція: 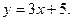
5. Побудувати графік функції: 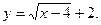
Варіант 2
1. Знайти область визначення функції: 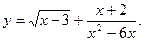
2. Знайти область значень функції: 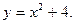
3. Визначити парна чи непарна функція: 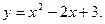
4. Визначити зростаюча чи спадна функція: 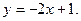
5. Побудувати графік функції: 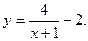
Варіант 3
1. Знайти область визначення функції: 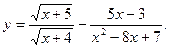
2. Знайти область значень функції: 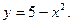
3. Визначити парна чи непарна функція: 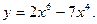
4. Визначити зростаюча чи спадна функція: 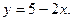
5. Побудувати графік функції: 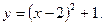
Варіант 4
1. Знайти область визначення функції: 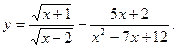
2. Знайти область значень функції: 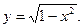
3. Визначити парна чи непарна функція: 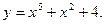
4. Визначити зростаюча чи спадна функція: 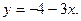
5. Побудувати графік функції: 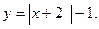
ІV. Підсумок. Домашнє завдання



 1. Відображення властивостей реального світу через поняття величини + допрацювати
1. Відображення властивостей реального світу через поняття величини + допрацювати
Величини відображають різноманітні властивості реального світу. У математиці поняття величини виникло в результаті абстрагування від якісних особливостей, властивостей реальних об'єктів, щоб виділити тільки кількісні відношення.
У процесі абстракції властивості об'єктів і явищ дещо ідеалізуються, відбувається деяке віддалення від дійсності, від окремих сторін явищ і об'єктів. У самій природі немає довжини, площі, сили, швидкості. Ці та інші величини вводяться в процесі пізнання для описання явищ природи. Тому величини - це не сама реальність, а лише її відображення. Багатовікова практика показує, що величини правильно відображають властивості об'єктів навколишнього середовища. Абстракція є засобом пізнання. Поняття величини тісно зв'язане з поняттям вимірювання. Результат вимірювання виражається числовим значенням величини при певній одиниці вимірювання - мірою величини. Вимірювання є одним з шляхів пізнання природи людиною, який поєднує теорію з практикою. Ще в давній давнині вимірюванням було знайдено багато емпіричних фактів про загальні властивості величин, які є відображенням властивостей дійсного світу.
Роль і значення вимірювань у процесі розвитку природничих і технічних наук безперервно зростає, бо зростає число і якість вимірюваних величин. Величини є складовою частиною змісту багатьох природничих наук — математики, фізики, астрономії, хімії, біології і ін.
Без величин та вимірювання їх вивчення природи, її властивостей, закономірностей обмежилось би тільки спостереженнями, залишилося на описовому рівні. Отже, величини дають змогу перейти від описового до кількісного вивчення властивостей об'єктів, тобто математизувати знання про
природу.
Відомо, що не кожну властивість об'єкта чи явища можна виміряти. Прикладами таких понять є поняття воля, сміливість, горе, щастя, радість, гнів. Іноді ці властивості теж називають величинами, але на відміну від звичайних — величинами латентними. Порівняння таких величин можливе тільки на деякій інтуїтивній основі, через систему поступків, поведінки; порівняння їх умовне, не числове. Над такими величинами не можна виконувати арифметичні дії.
Між різними властивостями об'єктів і явищ навколишньої дійсності існують певні зв'язки, частина з яких відображається в залежностях між відповідними величинами. Зв'язки величин, їх взаємозалежність виражаються формулами. Математична формула виражає в основному вид залежності між символами, які входять в неї. Самі символи можуть не мати конкретного змісту (аb = bа, 8=аk).
У фізичній формулі відображені зв'язки між величинами реального світу.
У процесі вивчення різних величин слід звернути увагу не тільки на їх числове значення, а й на ті властивості об'єктів, які характеризуються даними величинами. Наприклад, коли йдеться про площу трикутника, прямокутника, трапеції, то слід знати властивості цих фігур; коли йдеться про масу тіла, то треба мати на увазі не тільки число кілограмів, а й ті властивості, які відображає ця величина. Часто маса безпосередньо не асоціюється з властивостями інертності або гравітації, а існує як якесь самостійне поняття. Маса як фізична величина окремо від матерії не існує.
Вивчення взаємозв'язків між величинами дає змогу бачити не тільки якісні зв'язки різних сторін об'єктивної реальності, тобто на описовому рівні, а й оцінювати їх кількісно. На прикладі використання величин у науках можна ознайомитися з одним із шляхів математичних знань, з тією роллю, яку відіграють математичні методи у вивченні природи. Все це має важливе значення при формуванні правильних уявлень про взаємодію математики з іншими природничими науками.
Роль величин у пізнанні природи невпинно зростає, вони проникають у
такі традиційно «нематематичні» науки, як біологія, психологія, педагогіка,
соціологія і інші.
Поняття величини
Поняття величини вперше з'явилося у філософській літературі і пов'язувалося з дійсним числом. Число з'явилось генетично в процесі рахунку предметів і вимірювання величин (довжин, площ, об'ємів і ін.). На цю обставину вказував ще Арістотель (IV ст. до н. є.).
Предметом вивчення математики до XVII ст., як відомо, були сталі величини. Пізніше, коли виникла задача математичного описування процесів і рухів у фізиці та астрономії, були введені змінні величини. До середини минулого століття математика мала справу з величинами, але вивчала не конкретні властивості окремих величин, а загальні властивості та відношення об'єктів математичної природи, абстраговані від якісного змісту.
Проте як у філософській, так і в математичній літературі того часу, означення поняття величини в більшості випадків мали описовий характер. Наприклад, Л. Е й л є р називав величиною все те, що має здатність збільшуватись або зменшуватись. Аналогічно описує поняття величини і
А. Лебег. Французький енциклопедист д'Аламбер (XVIII ст.) визначав математику як науку, що вивчає властивості величин, оскільки вони перелічуються і вимірюються.
У процесі свого розвитку поняття величини уточнялося, узагальнювалося. Де Евклід у «Початках» дав перше узагальнення таких конкретних понять, як «довжина відрізка», «площа», «об'єм», та інших у вигляді аксіом. Ці аксіоми неявно визначають поняття додатної скалярної величини. Розширення цього поняття привело потім до понять скалярної, векторної і тензорної величин.
Академік О. Д. Александров дає таке означення величини: «Величиною взагалі називається така властивість предмета, явища або процесу, яка в якомусь відношенні може бути більшою або меншою, причому так, що є можливість точного порівняння» (тобто вимірювання при вибраній одиниці вимірювання). Величинами є довжина, площа, об'єм, маса, робота, сила світла, вартість. Не є величинами: горе, радість, любов, воля, героїзм - над ними не можна виконувати арифметичні дії.
Звичайно, поняття величини відіграє фундаментальну роль не лише в математиці, а й у фізиці, де предметом фізичного дослідження є фізичні об'єкти, явища, які мають багато властивостей. Для кількісного опису цих властивостей використовуються різні величини.
В елементарній математиці й фізиці розглядають скалярні й векторні величини.
Скалярними величинами називають такі величини, які повністю
характеризуються числовим значенням — числом. Це, наприклад, довжина,
площа, об'єм, маса, густина та ін.
Векторними величинами називають такі величини, для характеристики
яких, крім числового значення, необхідно вказувати ще й напрямок дії.
Такими є, зокрема, фізичні величини: швидкість, прискорення, сила та ін.
Геометрично векторні величини зображують напрямленими відрізками,
які називають векторами. Латинське слово уєсіог означає «тягти у певному
напрямку». Далі розглядатимемо лише скалярні величини (величини, які повністю характеризуються числовим значенням).
3. Адитивно-скалярні величини та їх властивості
Щоб дати означення й сформулювати властивості скалярних величин,
необхідно ввести поняття однорідних величин. Однорідними величинами
називають величини, які характеризують ту саму якість об'єктів. Наприклад,
однорідними величинами є всі довжини відрізків, усі площі фігур, усі маси тіл і т. д.
Для будь-якої системи однорідних величин повинно бути встановлено поняття рівності (а = b ) і нерівності (а < b або b > а). Довжини відрізків, наприклад, можна порівнювати за допомогою накладання, маси тіл — за допомогою терезів тощо.
Якщо в системі однорідних скалярних величин визначена операція додавання однорідних величин, яка дає змогу замінити дві однорідні величини а і b їхньою сумою а + b, то така система величин називається системою адитивно-скалярних величин. Суму п однакових доданків а + а + а +... + а позначатимемо через па.
Надалі розглядатимемо лише адитивно-скалярні величини. Поняття системи однорідних адитивно-скалярних величин можна ввести різними способами: за допомогою понять дійсного числа як функції із заданими властивостями та аксіоматично. Наведемо аксіоматичне означення. Основним об'єктом є величина, основним відношенням — відношення
доданків до суми.
Системою М однорідних адитивно-скалярних величин називається
система величин, яка характеризується такими аксіомами.
А1. Для довільних а, b Є М виконується один і тільки один з трьох
випадків: а = b а < b, b < а.
А2. (  а) (
а) (  b) (
b) (  с) (а < b
с) (а < b  b < с) => а < с; а, b, с Є М (транзитивність
b < с) => а < с; а, b, с Є М (транзитивність
