Ая интерполяционная формула Ньютона
Вариант
$$$1 Абсолютная величина разности между точным и приближённым значением числа называется:
$истинной погрешностью
$$абсолютной погрешностью
$истинной абсолютной погрешностью
$относительной погрешностью
$$$2 Формула вычисления истинной абсолютной погрешности имеет вид:
$$ 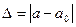
$ 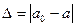
$ 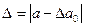
$ 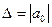
$$$3 Границей абсолютной погрешности называется число:
$$ 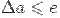
$ 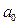
$ 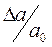
$ 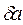
$$$4 Определение "Отношение границы абсолютной погрешности к модулю самого числа" относится к:
$относительной погрешности
$$границе относительной погрешности
$абсолютной ошибке
$границе абсолютной ошибки
$$$5 Формула относительной погрешности имеет вид:
$ 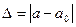
$ 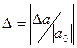
$$ 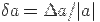
$ 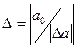
$$$6 Если точное число 245,21, а приближенное число 246, то истинной абсолютной погрешностью будет число:
$0,0031
$0,081
$0,013
$$0,79
$$$7 Если абсолютная погрешность числа не превосходит единицы этого разряда, то некоторая цифра приближённого числа называется:
$сомнительной
$верной
$абсолютной
$$относительной
$$$8 Если а=945,673, 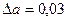 , то цифра 6 является
, то цифра 6 является
$верной
$сомнительной
$$абсолютной
$относительной
$$$9 Если а=142,5, 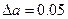 , то граница относительной погрешности:
, то граница относительной погрешности:
$$0,03%
$0,3%
$0,003%
$0,0003%
$$$10 Граница абсолютной погрешности числа а=1348, если 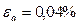 равна:
равна:
$0,539
$0,5
$$0,54
$0,53
$$$11 Если в матрице число столбцов равно числу строк, то матрица называется:
$прямоугольной
$векторной
$треугольной
$$квадратной
$$$12 Если в матрице число строк не равно числу столбцов то матрица называется
$квадратной
$треугольной
$векторной
$$прямоугольной
$$$13 Число строк или столбцов матрицы называется её
$рангом
$$порядком
$степенью
$диагональю
$$$14 Матрица, у которой все элементы, кроме главной диагонали, равны нулю называется:
$вектором
$единичной
$треугольной
$$диагональной
$$$15 Если у диагональной матрицы все элементы главной диагонали равны единице, то такая матрица является:
$скалярной
$$единичной
$нулевой
$векторной
$$$16 К векторам относятся:
$матрицы-строки
$диагональные матрицы
$единичные матрицы
$$скалярные матрицы
$$$17 Операция замены строк и столбцов матрицы называется:
$сложением
$понижением порядка
$$транспонированием
$вычитанием
$$$18 Дана матрица 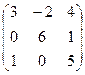 . Алгебраическим дополнением 3 элемента 2 строки является число:
. Алгебраическим дополнением 3 элемента 2 строки является число:
$1
$-1
$$2
$-2
$$$19 Дана матрица 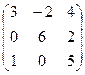 . Определитель данной матрицы равен:
. Определитель данной матрицы равен:
$$62
$24
$86
$90
$$$20 Для матриц несправедливо следующее арифметическое действие:
$сложение
$вычитание
$умножение
$$ деление
$$$21 Для вычисления определителя матрицы используют:
$$правило Саррюса
$правило Гаусса
$правило диагоналей
$правило Крамера
$$$22 Для умножения матриц не справедлив математический закон:
$Сочетательный
$Переместительный
$$Распределительный
$Коммутативный
$$$23 Если для матрицы А существует матрица -А, то она обратная
$$обратная
$противоположная
$транспонированная
$единичная
$$$24 Результатом сложения матрицы А и противоположной ей матрицы -А - является матрица...
$обратная
$единичная
$нулевая
$$транспонированная
$$$25 При транспонировании матрицы её определитель:
$$изменяется
$не изменяется
$меняет знак на противоположный
$равен 0
$$$26 Определитель матрицы 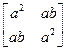 равен:
равен:
$$ 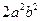
$ 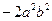
$ 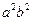
$0
$$$27 Найти произведение матриц А и В, если 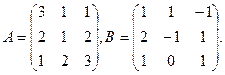 С=А*В
С=А*В
$ 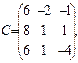
$ 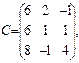
$ 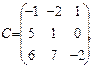
$$ 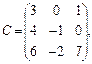
$$$28 Найти определитель матрицы С=А*В, если 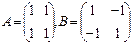
$1
$-1
$$0
$-2
$$$29 Алгебраическое дополнение 1 элемента 2 строки матрицы 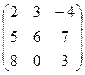
$$9
$-9
$5
$-5
$$$30 Новый определитель, который получается из определителя вычеркиванием строки и столбца, содержащих данный элемент называется:
$$алгебраическое дополнение
$минор
$матрица
$вектор
$$$31 Обратимой называется матрица...
$вырожденная
$$которой можно найти обратную матрицу
$единичная
$треугольная
$$$32 Найти обратную матрицу: 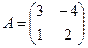
$ 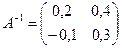
$ 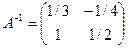
$$ 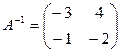
$ 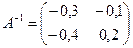
$$$33 Решить матричное уравнение: 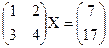
$$ 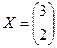
$ 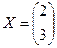
$ 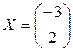
$ 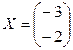
$$$34 Способ решения СЛАУ, заключающийся составлений матрицы из коэффициентов и вектора из свободных членов, с последующим нахождением обратной матрицы, является методом
$Гаусса
$Матричным
$Крамера
$$Сарруса
$$$35 Дана матрица 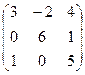 . Алгебраическим дополнением 3 элемента 2 строки является число:
. Алгебраическим дополнением 3 элемента 2 строки является число:
$1
$-1
$$2
$-2
$$$36 Дать объяснения на целой рациональной функций
$$переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем
$для получения значения функции по данному значению х нужно выполнить арифметические
$хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем
$ если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня
$$$37 Что такое минор?
$который вычисляется из элементов матрицы
$алгебраическое дополнение
$это строки и столбцы
$$определитель, полученный после вычеркивания из исходного строки и столбца,
на пересечении которых стоит этот элемент.
$$$38 Алгебраическое дополнение элемента – это…
$$минор этого элемента, взятый со знаком (+), если сумма номеров строки и столбца,
$будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя.
$который вычисляется из элементов матрицы
$алгебраическое дополнение
$$$39 Теорема Лапласа
$$сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d.
$будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя.
$однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю.
$предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа.
$$$40 Операция сложения матриц определяется…
$$для двух матриц одинакового размера
$алгебраического сложения соответствующих элементов матрицы
$предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа.
$если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
$$$41 Операция умножения матриц имеет смысл в том случае
$$когда количество столбцов первого сомножителя равно количеству строк второго сомножителя.
$комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
$ играет ключевую роль в решении в общем виде систем линейных уравнений, на его основе вводятся базовые понятия.
$ если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
$$$42 Степень матрицы
$$это матрица, полученная путём многократного умножения на саму себя
$понятие целой положительной степени матрицы
$имеет один столбец или одну строку.
$комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
$$$43 Частный случай умножения:
$одна из матриц-сомножителей имеет один столбец или одну строку.
$если считать матрицу строку или матрицу-столбец формой представления вектора
$то мы получаем правило умножения матрицы на вектор.
$$все ответы правильные
$$$44 Если А – это матрица, h – это скалярная величина
$то результатом умножения А на h считается такая матрица (hА)
$элементы которой получаются в результате умножения каждого элемента матрицы А на число h
$это же определение даёт правило деления матрицы на число
$$все ответы правильные
$$$45 Операция транспортирования матрицы-
$$это замена всех строк матрицы на столбцы, а всех столбцов - на строки.
$одна из матриц-сомножителей имеет один столбец или одну строку.
$понятие целой положительной степени матрицы
$это матрица, полученная путём многократного умножения на саму себя
$$$46 Квадратная матрица
$$это матрица, у которой количество строк и столбцов равно.
$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали.
$комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
$это матрица, полученная путём многократного умножения на саму себя
$$$47 Диагональная матрица
$$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали
$это матрица, у которой количество строк и столбцов равно
$это матрица, полученная путём многократного умножения на саму себя
$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали
$$$48 Единичная матрица
$$это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е.
$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали
$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали
$это матрица, у которой количество строк и столбцов равно
$$$49 Коммутативные матрицы
$$две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей
$это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е.
$это матрица, у которой количество строк и столбцов равно
$это матрица, полученная путём многократного умножения на саму себя
$$$50 Cимметричные матрицы.
$$что операция транспортирования матрицы не изменяет вид матрицы – матрица симметрична относительно своей главной диагонали.
$две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей
$это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е.
$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали
$$$51 Отделить корней это…
$$это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень
$кривая трижды пересекает ось абсцисс
$кривая касается оси абсцисс
$не обладает большой точностью
$$$52 Два способа, которое можно произвести отделение корней
$$графический и аналитический
$трансцендентные и алгебраические
$графический и алгебраический
$аналитический и трансцендентные
$$$53 Уравнение называется алгебраическим если…
$$в запись уравнения входят только алгебраические функции
$уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция
$если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня
$все ответы правильно
$$$54 Какая функция называется дробно-рациональной?
$$если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем
$если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня
$переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем
$уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция
$$$55 Какая функция называется иррациональной?
$$если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня
$уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция
$если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем
$если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем
$$$56 Функция y=f(x) называется возрастающей…
$$если с возрастанием аргумента значение функции увеличивается
$если является делителем
$если является дробной и иррациональной функции
$если переменная увеличивается, хотя бы один раз
$$$57 Функция y=f(x) называется убывающей…
$$если с возрастанием аргумента значение функции уменьшается
$если с возрастанием аргумента значение функции увеличивается
$если является дробной и иррациональной функции
$если переменная увеличивается, хотя бы один раз
$$$58 Функция называется монотонной
$$если она в заданном промежутке, либо только возрастает, либо только убывает
$если с возрастанием аргумента значение функции уменьшается
$если с возрастанием аргумента значение функции увеличивается
$все ответы правильно
$$$59 Пусть А=784,2737, а=784,274 тогда абсолютная погрешность
$$0,0003
$0,0004
$0,0005
$0,0006
$$$60 Система называется однородной…
$$если все её свободные члены равны нулю
$если все ее свободные члены равны единицу
$если выполняется диагональная матрица
$если выполняется клеточная матрица
$$$61 Система называется квадратной…
$$если число m уравнений равно числу n неизвестных.
$если число строк больше чем число столбец
$если выполняется обратная матрица
$если выполняется метод Гаусс
$$$62 Система называется совместной…
$$если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
$если выполняется обратная матрица
$если выполняется метод Гаусс
$если она имеет несколько решений
$$$63 В методе Рунге-Кутта, так же и в методе Эйлера, последовательные значения искомой функции определяются по формуле
$$ 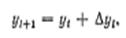
$ 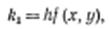
$ 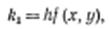
$ 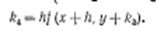
$$$64 Формула Симпсона называется…
$$интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:
$значение исходного интеграла является суммой результатов интегрирования на всех отрезках
$формулы вычислительной математики, применяющиеся для полиномиального интерполирования
$все ответы правильные
$$$65 Формула Симпсона
$$ 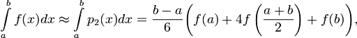
$ 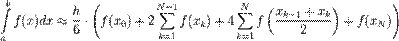
$ 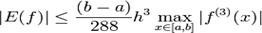
$ 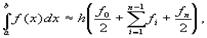
ая интерполяционная формула Ньютона
$$ 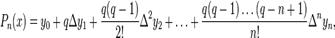
$ 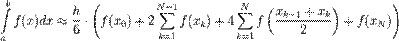
$ 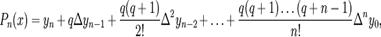
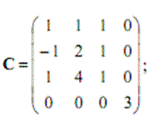 $
$ 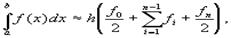
$$$67 Запишите элемент С24 матрицы С
$$0
$1
$3
$4
$$$68 Интерполяционный многочлен в форме Лагранжа
$$ 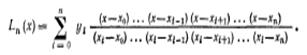
$ 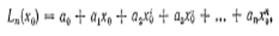
$ 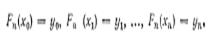
$ 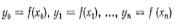
$$$69 Интерполяционный многочлен в форме Ньютона
$$ 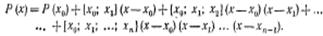
$ 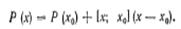
$ 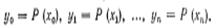
$ 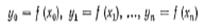
$$$70 Квадратурная формула трапеции
$$ 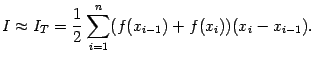
$ 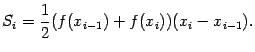
$ 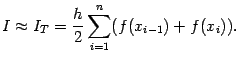
$ 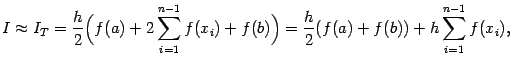
$$$71 Квадратурная формула Симпсона
$$ 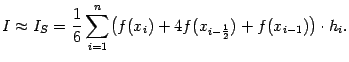
$ 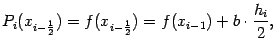
$ 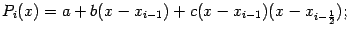
$ 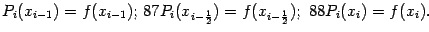 $$$72 Применение метода Монте-Карло для вычисления кратных интегралов $$вырабатывать последовательности случайных чисел с заданным законом распределения $выработки случайных чисел на ЭВМ $случайные с распределением форма которого максимально близка к форме интегрируемой функции $для определения различных физических параметров систем. $$$73 Виды погрешности $ неустранимая $ абсолютная, $относительная. $$ все ответы правильные $$$74 Число строк не равно числу столбцов то тогда матрица называется $квадратной $треугольной $векторной $$прямоугольной $$$75 Число строк или столбцов матрицы называется её $рангом $$порядком $степенью $диагональю $$$14 Матрица, у которой все элементы, кроме главной диагонали, равны нулю называется: $вектором $единичной $треугольной $$диагональной $$$15 Если у диагональной матрицы все элементы главной диагонали равны единице, то такая матрица является: $скалярной $$единичной $нулевой $векторной $$$16 К векторам относятся: $матрицы-строки $диагональные матрицы $единичные матрицы $$скалярные матрицы $$$17 Операция замены строк и столбцов матрицы называется: $сложением $понижением порядка $$транспонированием $вычитанием $$$18 Дана матрица $$$72 Применение метода Монте-Карло для вычисления кратных интегралов $$вырабатывать последовательности случайных чисел с заданным законом распределения $выработки случайных чисел на ЭВМ $случайные с распределением форма которого максимально близка к форме интегрируемой функции $для определения различных физических параметров систем. $$$73 Виды погрешности $ неустранимая $ абсолютная, $относительная. $$ все ответы правильные $$$74 Число строк не равно числу столбцов то тогда матрица называется $квадратной $треугольной $векторной $$прямоугольной $$$75 Число строк или столбцов матрицы называется её $рангом $$порядком $степенью $диагональю $$$14 Матрица, у которой все элементы, кроме главной диагонали, равны нулю называется: $вектором $единичной $треугольной $$диагональной $$$15 Если у диагональной матрицы все элементы главной диагонали равны единице, то такая матрица является: $скалярной $$единичной $нулевой $векторной $$$16 К векторам относятся: $матрицы-строки $диагональные матрицы $единичные матрицы $$скалярные матрицы $$$17 Операция замены строк и столбцов матрицы называется: $сложением $понижением порядка $$транспонированием $вычитанием $$$18 Дана матрица 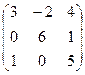 . Алгебраическим дополнением 3 элемента 2 строки является число: $1 $-1 $$2 $-2 $$$19 Дана матрица . Алгебраическим дополнением 3 элемента 2 строки является число: $1 $-1 $$2 $-2 $$$19 Дана матрица 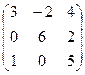 . Определитель данной матрицы равен: $$62 $24 $86 $90 $$$20 Для матриц несправедливо следующее арифметическое действие: $сложение $вычитание $умножение $$ деление $$$21 Для вычисления определителя матрицы используют: $$правило Саррюса $правило Гаусса $правило диагоналей $правило Крамера $$$22 Для умножения матриц не справедлив математический закон: $Сочетательный $Переместительный $$Распределительный $Коммутативный $$$23 Если для матрицы А существует матрица -А, то она обратная $$обратная $противоположная $транспонированная $единичная $$$24 Результатом сложения матрицы А и противоположной ей матрицы -А - является матрица... $обратная $единичная $нулевая $$транспонированная $$$25 При транспонировании матрицы её определитель: $$изменяется $не изменяется $меняет знак на противоположный $равен 0 $$$26 Определитель матрицы . Определитель данной матрицы равен: $$62 $24 $86 $90 $$$20 Для матриц несправедливо следующее арифметическое действие: $сложение $вычитание $умножение $$ деление $$$21 Для вычисления определителя матрицы используют: $$правило Саррюса $правило Гаусса $правило диагоналей $правило Крамера $$$22 Для умножения матриц не справедлив математический закон: $Сочетательный $Переместительный $$Распределительный $Коммутативный $$$23 Если для матрицы А существует матрица -А, то она обратная $$обратная $противоположная $транспонированная $единичная $$$24 Результатом сложения матрицы А и противоположной ей матрицы -А - является матрица... $обратная $единичная $нулевая $$транспонированная $$$25 При транспонировании матрицы её определитель: $$изменяется $не изменяется $меняет знак на противоположный $равен 0 $$$26 Определитель матрицы 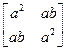 равен: $$ равен: $$ 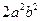 $ $ 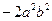 $ $ 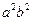 $0 $$$27 Найти произведение матриц А и В, если $0 $$$27 Найти произведение матриц А и В, если 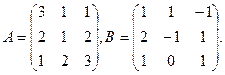 С=А*В $ С=А*В $ 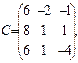 $ $ 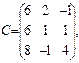 $ $ 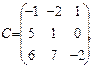 $$ $$ 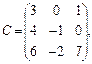 $$$28 Найти определитель матрицы С=А*В, если $$$28 Найти определитель матрицы С=А*В, если 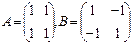 $1 $-1 $$0 $-2 $$$29 Алгебраическое дополнение 1 элемента 2 строки матрицы $1 $-1 $$0 $-2 $$$29 Алгебраическое дополнение 1 элемента 2 строки матрицы 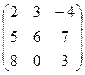 $$9 $-9 $5 $-5 $$$30 Новый определитель, который получается из определителя вычеркиванием строки и столбца, содержащих данный элемент называется: $$алгебраическое дополнение $минор $матрица $вектор $$$31 Обратимой называется матрица... $вырожденная $$которой можно найти обратную матрицу $единичная $треугольная $$$32 Найти обратную матрицу: $$9 $-9 $5 $-5 $$$30 Новый определитель, который получается из определителя вычеркиванием строки и столбца, содержащих данный элемент называется: $$алгебраическое дополнение $минор $матрица $вектор $$$31 Обратимой называется матрица... $вырожденная $$которой можно найти обратную матрицу $единичная $треугольная $$$32 Найти обратную матрицу: 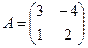 $ $ 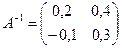 $ $ 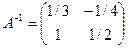 $$ $$ 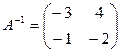 $ $ 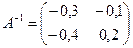 $$$33 Решить матричное уравнение: $$$33 Решить матричное уравнение: 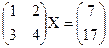 $$ $$ 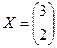 $ $ 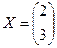 $ $ 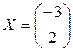 $ $ 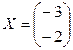 $$$34 Способ решения СЛАУ, заключающийся составлений матрицы из коэффициентов и вектора из свободных членов, с последующим нахождением обратной матрицы, является методом $Гаусса $Матричным $Крамера $$Сарруса $$$35 Дана матрица $$$34 Способ решения СЛАУ, заключающийся составлений матрицы из коэффициентов и вектора из свободных членов, с последующим нахождением обратной матрицы, является методом $Гаусса $Матричным $Крамера $$Сарруса $$$35 Дана матрица 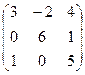 . Алгебраическим дополнением 3 элемента 2 строки является число: $1 $-1 $$2 $-2 $$$36 Дать объяснения на целой рациональной функций $$переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем $для получения значения функции по данному значению х нужно выполнить арифметические $хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $ если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $$$37 Что такое минор? $который вычисляется из элементов матрицы $алгебраическое дополнение $это строки и столбцы $$определитель, полученный после вычеркивания из исходного строки и столбца, на пересечении которых стоит этот элемент. $$$38 Алгебраическое дополнение элемента – это… $$минор этого элемента, взятый со знаком (+), если сумма номеров строки и столбца, $будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя. $который вычисляется из элементов матрицы $алгебраическое дополнение $$$39 Теорема Лапласа $$сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d. $будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя. $однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю. $предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа. $$$40 Операция сложения матриц определяется… $$для двух матриц одинакового размера $алгебраического сложения соответствующих элементов матрицы $предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа. $если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. $$$41 Операция умножения матриц имеет смысл в том случае $$когда количество столбцов первого сомножителя равно количеству строк второго сомножителя. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $ играет ключевую роль в решении в общем виде систем линейных уравнений, на его основе вводятся базовые понятия. $ если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. $$$42 Степень матрицы $$это матрица, полученная путём многократного умножения на саму себя $понятие целой положительной степени матрицы $имеет один столбец или одну строку. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $$$43 Частный случай умножения: $одна из матриц-сомножителей имеет один столбец или одну строку. $если считать матрицу строку или матрицу-столбец формой представления вектора $то мы получаем правило умножения матрицы на вектор. $$все ответы правильные $$$44 Если А – это матрица, h – это скалярная величина $то результатом умножения А на h считается такая матрица (hА) $элементы которой получаются в результате умножения каждого элемента матрицы А на число h $это же определение даёт правило деления матрицы на число $$все ответы правильные $$$45 Операция транспортирования матрицы- $$это замена всех строк матрицы на столбцы, а всех столбцов - на строки. $одна из матриц-сомножителей имеет один столбец или одну строку. $понятие целой положительной степени матрицы $это матрица, полученная путём многократного умножения на саму себя $$$46 Квадратная матрица $$это матрица, у которой количество строк и столбцов равно. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $это матрица, полученная путём многократного умножения на саму себя $$$47 Диагональная матрица $$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой количество строк и столбцов равно $это матрица, полученная путём многократного умножения на саму себя $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $$$48 Единичная матрица $$это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой количество строк и столбцов равно $$$49 Коммутативные матрицы $$две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей $это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой количество строк и столбцов равно $это матрица, полученная путём многократного умножения на саму себя $$$50 Cимметричные матрицы. $$что операция транспортирования матрицы не изменяет вид матрицы – матрица симметрична относительно своей главной диагонали. $две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей $это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $$$51 Отделить корней это… $$это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень $кривая трижды пересекает ось абсцисс $кривая касается оси абсцисс $не обладает большой точностью $$$52 Два способа, которое можно произвести отделение корней $$графический и аналитический $трансцендентные и алгебраические $графический и алгебраический $аналитический и трансцендентные $$$53 Уравнение называется алгебраическим если… $$в запись уравнения входят только алгебраические функции $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $все ответы правильно $$$54 Какая функция называется дробно-рациональной? $$если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $$$55 Какая функция называется иррациональной? $$если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $$$56 Функция y=f(x) называется возрастающей… $$если с возрастанием аргумента значение функции увеличивается $если является делителем $если является дробной и иррациональной функции $если переменная увеличивается, хотя бы один раз $$$57 Функция y=f(x) называется убывающей… $$если с возрастанием аргумента значение функции уменьшается $если с возрастанием аргумента значение функции увеличивается $если является дробной и иррациональной функции $если переменная увеличивается, хотя бы один раз $$$58 Функция называется монотонной $$если она в заданном промежутке, либо только возрастает, либо только убывает $если с возрастанием аргумента значение функции уменьшается $если с возрастанием аргумента значение функции увеличивается $все ответы правильно $$$59 Пусть А=784,2737, а=784,274 тогда абсолютная погрешность $$0,0003 $0,0004 $0,0005 $0,0006 $$$60 Система называется однородной… $$если все её свободные члены равны нулю $если все ее свободные члены равны единицу $если выполняется диагональная матрица $если выполняется клеточная матрица $$$61 Система называется квадратной… $$если число m уравнений равно числу n неизвестных. $если число строк больше чем число столбец $если выполняется обратная матрица $если выполняется метод Гаусс $$$62 Система называется совместной… $$если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. $если выполняется обратная матрица $если выполняется метод Гаусс $если она имеет несколько решений $$$63 В методе Рунге-Кутта, так же и в методе Эйлера, последовательные значения искомой функции определяются по формуле $$ . Алгебраическим дополнением 3 элемента 2 строки является число: $1 $-1 $$2 $-2 $$$36 Дать объяснения на целой рациональной функций $$переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем $для получения значения функции по данному значению х нужно выполнить арифметические $хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $ если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $$$37 Что такое минор? $который вычисляется из элементов матрицы $алгебраическое дополнение $это строки и столбцы $$определитель, полученный после вычеркивания из исходного строки и столбца, на пересечении которых стоит этот элемент. $$$38 Алгебраическое дополнение элемента – это… $$минор этого элемента, взятый со знаком (+), если сумма номеров строки и столбца, $будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя. $который вычисляется из элементов матрицы $алгебраическое дополнение $$$39 Теорема Лапласа $$сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d. $будет сформулировано после введения понятий миноров и алгебраических дополнений элементов определителя. $однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю. $предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа. $$$40 Операция сложения матриц определяется… $$для двух матриц одинакового размера $алгебраического сложения соответствующих элементов матрицы $предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа. $если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. $$$41 Операция умножения матриц имеет смысл в том случае $$когда количество столбцов первого сомножителя равно количеству строк второго сомножителя. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $ играет ключевую роль в решении в общем виде систем линейных уравнений, на его основе вводятся базовые понятия. $ если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. $$$42 Степень матрицы $$это матрица, полученная путём многократного умножения на саму себя $понятие целой положительной степени матрицы $имеет один столбец или одну строку. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $$$43 Частный случай умножения: $одна из матриц-сомножителей имеет один столбец или одну строку. $если считать матрицу строку или матрицу-столбец формой представления вектора $то мы получаем правило умножения матрицы на вектор. $$все ответы правильные $$$44 Если А – это матрица, h – это скалярная величина $то результатом умножения А на h считается такая матрица (hА) $элементы которой получаются в результате умножения каждого элемента матрицы А на число h $это же определение даёт правило деления матрицы на число $$все ответы правильные $$$45 Операция транспортирования матрицы- $$это замена всех строк матрицы на столбцы, а всех столбцов - на строки. $одна из матриц-сомножителей имеет один столбец или одну строку. $понятие целой положительной степени матрицы $это матрица, полученная путём многократного умножения на саму себя $$$46 Квадратная матрица $$это матрица, у которой количество строк и столбцов равно. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали. $комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. $это матрица, полученная путём многократного умножения на саму себя $$$47 Диагональная матрица $$это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой количество строк и столбцов равно $это матрица, полученная путём многократного умножения на саму себя $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $$$48 Единичная матрица $$это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $это матрица, у которой количество строк и столбцов равно $$$49 Коммутативные матрицы $$две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей $это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой количество строк и столбцов равно $это матрица, полученная путём многократного умножения на саму себя $$$50 Cимметричные матрицы. $$что операция транспортирования матрицы не изменяет вид матрицы – матрица симметрична относительно своей главной диагонали. $две матрицы называются коммутативными, если произведение матриц не зависит от порядка сомножителей $это диагональная матрица, у которой все элементы на главной диагонали равны 1, обычно единичную матрицу обозначают буквой Е. $это матрица, у которой равны нулю все элементы, кроме элементов на главной диагонали $$$51 Отделить корней это… $$это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень $кривая трижды пересекает ось абсцисс $кривая касается оси абсцисс $не обладает большой точностью $$$52 Два способа, которое можно произвести отделение корней $$графический и аналитический $трансцендентные и алгебраические $графический и алгебраический $аналитический и трансцендентные $$$53 Уравнение называется алгебраическим если… $$в запись уравнения входят только алгебраические функции $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $все ответы правильно $$$54 Какая функция называется дробно-рациональной? $$если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $переменная х не входит в качестве делителя или не входит в выражение, являющимся делителем $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $$$55 Какая функция называется иррациональной? $$если, для получения значения функции по данному значению х нужно выполнить кроме четырех арифметических действий, еще и извлечение корня $уравнение получено преобразованием уравнения, в которое входило дробная рациональная или иррациональная функция $если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $если в рациональной функций, хотя бы один раз встречается деление на переменную х или переменная х входит в выражение, являющееся делителем $$$56 Функция y=f(x) называется возрастающей… $$если с возрастанием аргумента значение функции увеличивается $если является делителем $если является дробной и иррациональной функции $если переменная увеличивается, хотя бы один раз $$$57 Функция y=f(x) называется убывающей… $$если с возрастанием аргумента значение функции уменьшается $если с возрастанием аргумента значение функции увеличивается $если является дробной и иррациональной функции $если переменная увеличивается, хотя бы один раз $$$58 Функция называется монотонной $$если она в заданном промежутке, либо только возрастает, либо только убывает $если с возрастанием аргумента значение функции уменьшается $если с возрастанием аргумента значение функции увеличивается $все ответы правильно $$$59 Пусть А=784,2737, а=784,274 тогда абсолютная погрешность $$0,0003 $0,0004 $0,0005 $0,0006 $$$60 Система называется однородной… $$если все её свободные члены равны нулю $если все ее свободные члены равны единицу $если выполняется диагональная матрица $если выполняется клеточная матрица $$$61 Система называется квадратной… $$если число m уравнений равно числу n неизвестных. $если число строк больше чем число столбец $если выполняется обратная матрица $если выполняется метод Гаусс $$$62 Система называется совместной… $$если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. $если выполняется обратная матрица $если выполняется метод Гаусс $если она имеет несколько решений $$$63 В методе Рунге-Кутта, так же и в методе Эйлера, последовательные значения искомой функции определяются по формуле $$ 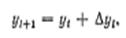 $ $ 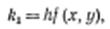 $ $ 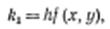 $ $ 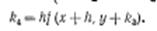 $$$64 Формула Симпсона называется… $$интеграл от интерполяционного многочлена второй степени на отрезке [a,b]: $значение исходного интеграла является суммой результатов интегрирования на всех отрезках $формулы вычислительной математики, применяющиеся для полиномиального интерполирования $все ответы правильные $$$65 Формула Симпсона $$ $$$64 Формула Симпсона называется… $$интеграл от интерполяционного многочлена второй степени на отрезке [a,b]: $значение исходного интеграла является суммой результатов интегрирования на всех отрезках $формулы вычислительной математики, применяющиеся для полиномиального интерполирования $все ответы правильные $$$65 Формула Симпсона $$ 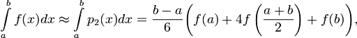 $ $ 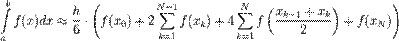 $ $ 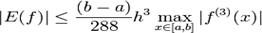 $ $ 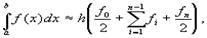 $$$66 1-ая интерполяционная формула Ньютона $$ $$$66 1-ая интерполяционная формула Ньютона $$ 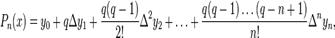 $ $ 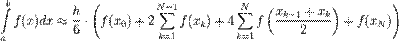 $ $ 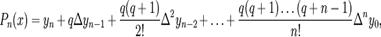 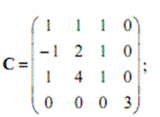 $ $ 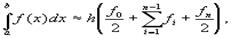 $$$67 Запишите элемент С24 матрицы С $$0 $1 $3 $4 $$$68 Интерполяционный многочлен в форме Лагранжа $$ $$$67 Запишите элемент С24 матрицы С $$0 $1 $3 $4 $$$68 Интерполяционный многочлен в форме Лагранжа $$ 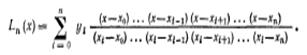 $ $ 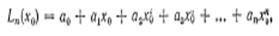 $ $ 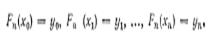 $ $ 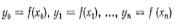 $$$69 Интерполяционный многочлен в форме Ньютона $$ $$$69 Интерполяционный многочлен в форме Ньютона $$ 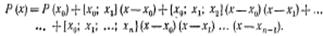 $ $ 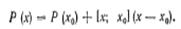 $ $ 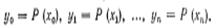 $ $ 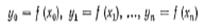 $$$70 Квадратурная формула трапеции $$ $$$70 Квадратурная формула трапеции $$ 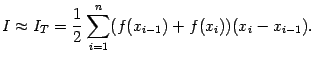 $ $ 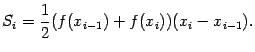 $ $ 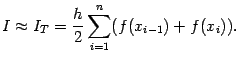 $ $ 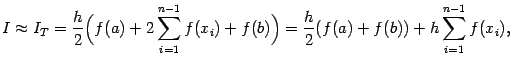 $$$71 Квадратурная формула Симпсона $$ $$$71 Квадратурная формула Симпсона $$ 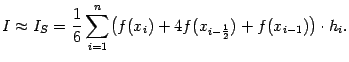 $ $ 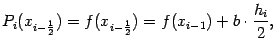 $ $ 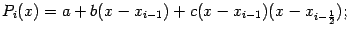
|
