Комплексные передаточные ф-ции для эл цепей

Комплексная передаточная ф-ция пред-ет собой отношение комплексной амплитуды р-ции (действующ значения р-ции) к комплексной амплитуде воздействия (действующ знаечнию возздействия)

1. Комплексная передаточная ф-ция по напряжению:

2. Комплексная передаточная ф-ция по току:

3. Комплексное передаточное сопротивление:

4. Комплексная передаточная проводимость:

Если и реак-ци яи воздействие приложены к одним и тем же зажима, то комплексные передаточные ф-ции превр-ся в входные

Зав-ть модуля комплексной передаточной ф-ции от частоты наз. АЧХ

Зав-ть аргумента к.п.ф. от частоты – ФЧХГраничная частота – чатсота, при к-ой активная составляющая= реактивной

Годограф – кривая, точки к-ой соотв-ют при данной частоте АЧх и ФЧХ

Индуктивно связанные цепи

: изучение методов расчета электрических цепей с взаимной индуктивностью.

10.1 Индуктивно связанные элементы цепи

Два элемента индуктивно связаны, если изменение тока в одном элементе приводит к появлению э.д.с. в другом элементе. Возникающая э.д.с. называется э.д.с. взаимной индукции (рисунок 10.1,а,б).

а) б)

Рисунок 10.1

При наличии тока i₁ в первой катушке, витки первой катушки сцеплены с магнитным потоком самоиндукции Ф₁₁, а витки второй катушки сцеплены с

магнитным потоком взаимной индукции Ф₂₁. (рисунок 10.1).

Потокосцепления самоиндукции и взаимной индукции первой и второй катушек ,

где w₁,w₂- число витков первой и второй катушек. При наличии тока i₂ во второй катушке, витки второй катушки сцеплены с магнитным потоком самоиндукции Ф₂₂, а витки первой катушки сцеплены с магнитным потоком взаимной индукции Ф₁₂. Потокосцепления самоиндукции и взаимной индукции второй и первой катушек: ; , где w₁,w₂- число витков первой и второй катушек. Индуктивность первой и второй катушек и их взаимная индуктивность определяются по формулам

, , , , . (10.1)

Степень индуктивной связи двух индуктивно связанных элементов цепи характеризуется коэффициентом связи

. (10.2)

10.2 Электродвижущая сила (э.д.с.) и напряжение взаимной индукции

При изменении тока в одном из индуктивно связанных элементов в другом элементе возникает э.д.с. взаимной индукции е_м и на его разомкнутых выводах появляется напряжение u_м:

; . (10.3)

Для определения знака е_м и u_м делают специальную разметку выводов индуктивно связанных элементов.

Два вывода принадлежащие двум разным индуктивно связанным элементам называются одноимёнными и обозначаются одинаковыми значками: _**, ,∆∆, если при одинаковом направлении токов в обоих элементах относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе складываются.

При одинаковом направлении тока в элементе 2, , в элементе 1 и тока в элементе 1, , в элементе 2 (рисунок 10.1,а) , , (10.4) , . (10.5)

Напряжение взаимной индукции опережает ток на , напряжение взаимной индукции опережает ток на .

При различном направлении тока в элементе 2, , в элементе 1 и тока в элементе 1, , в элементе 2 (рисунок 10.1,б) , . (10.6)

, . (10.7)

Напряжение взаимной индукции отстаёт от тока на , напряжение взаимной индукции отстаёт от тока на .

Величина называется сопротивлением взаимной индукции,

величина 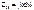называется комплексным сопротивлением взаимнойиндукции.