Системы линейных алгебраических уравнений

Система 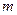линейных уравнений с 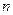переменными имеет вид: 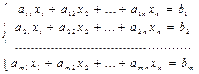, где 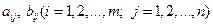- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

Решением системы называется такая совокупность 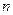чисел ( 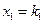, , 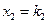…, 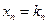), при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Система 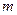линейных уравнений с 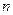переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид: .

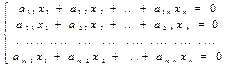Определение. Система линейно независимых решений 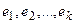называется фундаментальной, если каждое решение системы является линейной комбинацией решений .

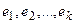Теорема. Если ранг 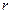матрицы коэффициентов при переменных системы линейных однородных уравнении меньше числа переменных 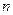, то всякая фундаментальная система решений состоит из 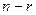решений.

Минор, алгебраичекоедопонение, ранг, их применение

Миноры и алгебраические дополнения. Теорема разложения.

Пусть имеем определитель третьего порядка: .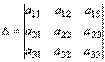

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель 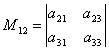, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

.

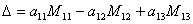(1)

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическим дополнением элемента a_ij определителя называется его минор M_ij, умноженный на (–1)^i+j.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1)^i+jM_ij.

ТЕОРЕМА РАЗЛОЖЕНИЯ