Решение квадратных уравнений

Одна из причин введения комплексных чисел состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в частности уравнения

x² = – 1.

Покажем, что расширив поле действительных чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное уравнение разрешимо, т.е. имеет решение. Так, уравнение x² = – 1 имеет два решения: x₁ = i, x₂ = – i.

Это нетрудно установить проверкой: i•i = i² = – 1, (– i)•(– i) = i² = – 1.

Перейдем теперь к вопросу о решении полного квадратного уравнения. Квадратным уравнением называют уравнение вида:

ax² + bx + c = 0 (a  0),

где x – неизвестная, a, b, c – действительные числа, соответственно первый, второй коэффициенты и свободный член, причем a  0. Решим это уравнение, выполнив над ним ряд несложных преобразований.

· Разделим все члены уравнения на a  0 и перенесем свободный член в правую часть уравнения: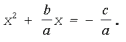

• К обеим частям уравнения прибавим выражение 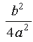с тем, чтобы левая его часть представляла полный квадрат суммы двух слагаемых: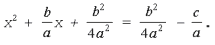
• Извлечем корень квадратный из обеих частей уравнения:
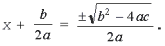
• Найдем значения неизвестной:

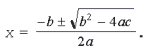
Теперь можно исследовать полученное решение. Оно зависит от значения подкоренного выражения, называемого дискриминантом квадратного уравнения. Если b² – 4ac > 0, то 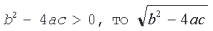есть действительное число и квадратное уравнение имеет действительные корни. Если же 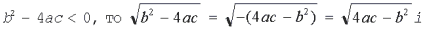– мнимое число, квадратное уравнение имеет мнимые корни.

Результаты исследования представлены ниже в таблице:

Итак, введение комплексных чисел позволяет разработать полную теорию квадратных уравнений. В поле комплексных чисел разрешимо любое квадратное уравнение.

Примеры.

1. Решите уравнение x² – 2x – 8 = 0.

Решение. Найдем дискриминант D = b² – 4ac = (– 2)² – 4•1•(– 8) = 36 > 0.

Уравнение имеет два действительных корня: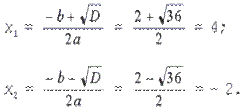

2. Решите уравнение x² + 6x + 9 = 0.

Решение. D = 6² – 4•1•9 = 0, уравнение имеет два равных действительных корня: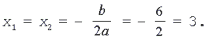

3. Решите уравнение x² – 4x + 5 = 0.

Решение. D = 16 – 4•1•5 = – 4 < 0, уравнение имеет мнимые корни: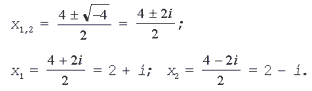

Геометрическая интерпретация комплексных чисел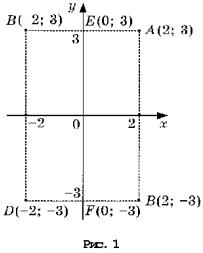

Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные и отрицательные температуры, передвижения в противоположных направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо проявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.

Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.

Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.

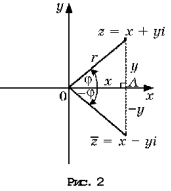
На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi, где y  0 – точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной. Сопряженным комплексным числам 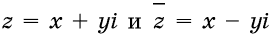соответствуют точки, симметричные относительно оси абсцисс (рис. 2).

Тригонометрическая форма комплексного числа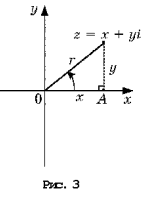

Точка координатной плоскости, соответствующая комплексному числу z = x + yi, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла j между положительной полуосью Ox и лучом Oz (рис. 3).

Расстояние r от начала системы координат до точки, соответствующей комплексному числу z, называют модулем этого числа. Тогда по теореме Пифагора (рис. 2) имеем: r² = x² + y² = (x + yi)(x – yi) = z•z.

Отсюда найдем модуль комплексного числа как арифметическое (неотрицательное) значение корня: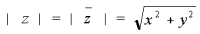

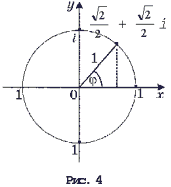
Если комплексное число z изображается точкой оси абсцисс (т.е. является действительным числом), то его модуль совпадает с абсолютным значением. Все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности – окружности с центром в начале системы координат, радиуса 1 (рис. 4).

Угол  между положительной полуосью Ox и лучом Oz называют аргументом комплексного числа z = x + yi (рис. 3).

Сопряженные комплексные числа 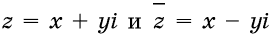имеют один и тот же модуль 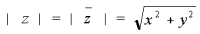и аргументы, отличающиеся знаком:  = – .

В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений, отличающихся друг от друга на число, кратное 360°. Например, число z (рис. 3) имеет модуль r, аргумент же этого числа может принимать значения j;  + 360°;  + 720°;  + 1080°; … или значения  – 360°;  –720°;  – 1080°; … Данное значение модуля r и любое из приведенных выше значений аргумента определяют одну и ту же точку плоскости, соответствующую числу z.

Пусть точке с координатами (x; y) соответствует комплексное число z = x + yi. Запишем это комплексное число через его модуль и аргумент. Воспользуемся определением тригонометрических функций синуса и косинуса (рис. 3):

x = r cos ; y = r sin .

Тогда число z выражается через модуль и аргумент следующим образом: z = x + yi = r(cos  + i sin ).

Выражение z = r(cos  + i sin ) называют тригонометрической формой комплексного числа, в отличии от выражения z = x + yi, называемого алгебраической формой комплексного числа.

Приведем примеры обращения комплексных чисел из алгебраической формы в тригонометрическую:

Для числа i имеем r = 1,  = 90°, поэтому i = 1(cos 90° + i sin 90°);

Для числа – 1 имеем r = 1,  = 180°, поэтому – 1 = 1(cos 180° + i sin 180°);

Для числа 1 + i имеем 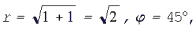поэтому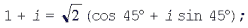

Для числа 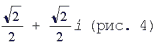имеем r = 1,  = 45°, поэтому

Для числа 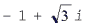имеем r = 2,  = 120°, поэтому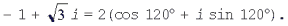

Справедливость приведенных равенств нетрудно проверить путем подстановки в их правой части числовых значений тригонометрических функций. Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент j, пользуясь формулами:

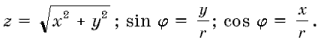
Натуральное число

Натуральные числа — числа, которые человек использует при счете предметов.

Существуют два подхода к определению натуральных чисел — числа, используемые при :

§ перечислении (нумеровании) предметов (первый, второй, третий…) — подход общепринятый в большинстве стран мира (в том числе и в России).

§ обозначении количества предметов (нет предметов, один предмет, два предмета… ) общепринято в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств.

Отрицательные и нецелые числа — натуральными числами не являются.

Множество всех натуральных чисел принято обозначать знаком .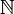

Существует бесконечное множество натуральных чисел — для любого натурального числа найдётся другое натуральное число, большее его.

Аксиомы Пеано

Введём функцию 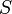, которая сопоставляет числу 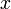следующее за ним число.

1. 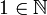( 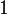является натуральным числом);

2. Если 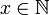, то 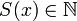(Число, следующее за натуральным, также является натуральным);

3. 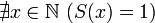(1 не следует ни за каким натуральным числом);

4. Есл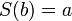и и 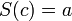, тогда 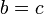(если натуральное число 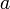непосредственно следует как за числом 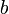, так и за числом , то );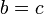

5. Аксиома индукции. Пусть 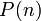— некоторый одноместный предикат, зависящий от параметра — натурального числа 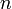. Тогда:

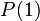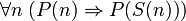если и , то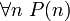

(Если некоторое высказывание 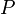верно для 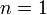(база индукции) и для любого 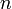при допущении, что верно 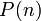, верно и 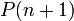(индукционное предположение), то 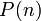верно для любых натуральных ).

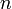Замечание

Иногда, в иностранной и переводной литературе, в первой и третьей аксиомах заменяют 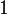на 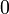. В этом случае ноль считается натуральным числом.