Элементы теории классов групп
Глава 1. Определения, обозначения и известные результаты, используемые в работе.
Элементы теории групп.
Определение 1. Под множеством понимают совокупность объектов, рассматриваемых как единое целое.
Определение 2. Множество, содержащее хотя бы один элемент, называется непустым.
Определение 3. Множество М называется конечным, если оно содержит конечное число элементов.
Определение 4. Пересечением множеств А и В называется множество, состоящие из всех элементов принадлежащих и множеству А и множеству В одновременно. Обозначается АÇВ, т.е. АÇВ={x | xÎА и xÎВ}.
Определение 5. Бинарное отношение f между множествами A и B называется функциональным отношением, если из (a,b) 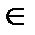 f и (a,c)
f и (a,c) 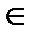 f следует, что b=c
f следует, что b=c 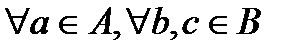 .
.
Определение 6. Функциональное отношение f между множествами A и B называется функцией или отображением A в B, если Dom f=A, и обозначается f : A 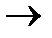 B или A
B или A 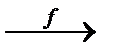 B.
B.
Замечание. Если f: A 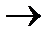 B – функция, то каждому элементу a
B – функция, то каждому элементу a 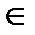 A соответствует единственный элемент b
A соответствует единственный элемент b 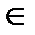 B и записывается f(a)=b
B и записывается f(a)=b 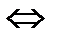 (a,b)
(a,b) 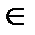 f
f 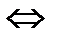 afb.
afb.
Определение 7. Пусть 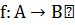 – отображение. Отображение
– отображение. Отображение 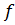 называется сюрьективным, если
называется сюрьективным, если 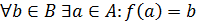 , то есть
, то есть 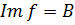 .
.
Определение 8. Отображение f : A 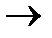 B называется инъективным, если из
B называется инъективным, если из 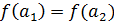 всегда следует, что
всегда следует, что 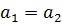 .
.
Определение 9. Отображение f : A 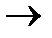 B называется биективным, если оно сюрьективно и инъективно.
B называется биективным, если оно сюрьективно и инъективно.
Определение 10. Пусть f : A 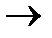 B – отображение. Если
B – отображение. Если 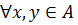
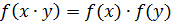 , то f называется гомоморфным отображением множества
, то f называется гомоморфным отображением множества 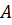 в
в 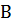 .
.
Если 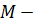 подмножество группы A, то
подмножество группы A, то 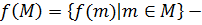 образ
образ 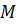 при гомоморфизме
при гомоморфизме 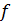 , а
, а 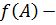 образ гомоморфизма
образ гомоморфизма 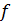 , который обозначают через
, который обозначают через 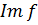 .
.
Ядром гомоморфизма 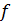 называется множество
называется множество 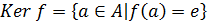 , где
, где 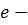 единичный элемент группы B.
единичный элемент группы B.
Через 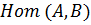 обозначают множество всех гомоморфизмов группы
обозначают множество всех гомоморфизмов группы 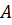 на группу
на группу 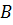 .
.
Определение 11. Гомоморфное отображение f множества 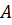 в
в 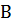 называется изоморфизмом, если f – биекция.
называется изоморфизмом, если f – биекция.
Теорема 1 (основная о гомоморфизмах).
Пусть 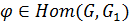 . Тогда
. Тогда 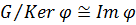 .
.
Теорема 2. Пусть 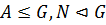 . Тогда
. Тогда 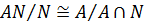 .
.
Теорема 3. Пусть 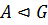 ,
, 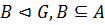 . Тогда
. Тогда 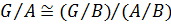 .
.
Теорема 4 (об естественном гомоморфизме).
Пусть 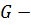 группа,
группа, 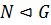 . Тогда существует гомоморфизм
. Тогда существует гомоморфизм 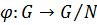 такой, что
такой, что 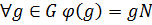 , который называется естественным гомоморфизмом.
, который называется естественным гомоморфизмом.
Определение 12. Бинарной алгебраической операцией на множестве М называется отображение 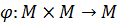 .
.
Определение 13. Бинарной алгебраической операцией на непустом множестве М называется закон или правило, по которому любым двум элементам множества М, не обязательно различным, взятым в определенном порядке, ставится в соответствие единственный элемент множества М. Обозначается: φ(a, b)=c.
Замечание. Если на множестве М задана бинарная алгебраическая операция «∗», то для любых 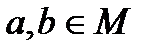 существует единственный элемент
существует единственный элемент 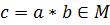 . В этом случае говорят, что множество М замкнуто относительно операции «∗».
. В этом случае говорят, что множество М замкнуто относительно операции «∗».
Говорят, что на множестве 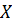 определена бинарная алгебраическая операция (умножение), если
определена бинарная алгебраическая операция (умножение), если 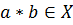 для всех
для всех 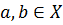 .
.
Определение 14. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Элемент 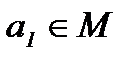 называется правым (левым) симметричным элементом для элемента
называется правым (левым) симметричным элементом для элемента 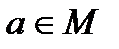 относительно операции «∗», если
относительно операции «∗», если 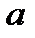 ∗
∗ 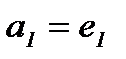 (
( 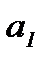 ∗
∗ 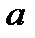
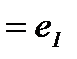 ), где
), где 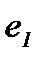 - правый (левый) нейтральный элемент множества М относительно операции «∗».
- правый (левый) нейтральный элемент множества М относительно операции «∗».
Определение 15. Если правый симметричный элемент 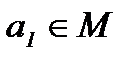 для элемента
для элемента 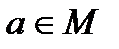 относительно операции «∗» является и левым симметричным элементом, то
относительно операции «∗» является и левым симметричным элементом, то 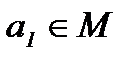 называется симметричным для
называется симметричным для 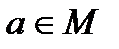 элементом, причем
элементом, причем 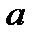 ∗
∗ 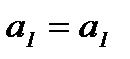 ∗
∗ 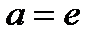 .
.
Определение 16. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Элемент 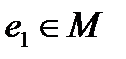 называется правым (левым) нейтральным элементом относительно операции «∗», если
называется правым (левым) нейтральным элементом относительно операции «∗», если 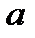 ∗
∗ 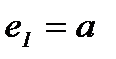 (
( 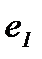 ∗
∗ 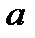
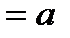 ) для любого
) для любого 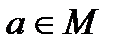 .
.
Определение 17. Если элемент 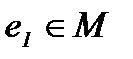 является правым и левым нейтральным элементом относительно операции «∗», то он называется нейтральным элементом в М относительно операции «∗», причем для любого
является правым и левым нейтральным элементом относительно операции «∗», то он называется нейтральным элементом в М относительно операции «∗», причем для любого 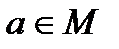
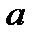 ∗
∗ 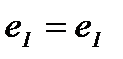 ∗
∗ 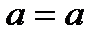 .
.
Замечание. Правый (левый) нейтральный элемент относительно операции «⋅» называется правым (левым) единичным элементом, а правый (левый) симметричный элемент для элемента а - правым (левым) обратным к а и обозначается а-1.
Определение 18. Пусть «∗» – бинарная алгебраическая операция на непустом множестве М. Операция «∗» называется
· коммутативной на множестве М, если  a,b
a,b 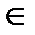 М: a∗b = b∗a.
М: a∗b = b∗a.
· ассоциативной на множестве М, если  a, b, c
a, b, c 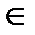 М:
М:
(a∗b)∗c =a∗(b∗c).
Определение 19. Непустое множество  , замкнутое относительно бинарной алгебраической операции «∗» называется группой, если выполняются следующие аксиомы (аксиомы группы):
, замкнутое относительно бинарной алгебраической операции «∗» называется группой, если выполняются следующие аксиомы (аксиомы группы):
1) операция «∗» ассоциативна на  ,т. е. а∗(b∗c) = (a∗b)∗c для любых a, b, c∈
,т. е. а∗(b∗c) = (a∗b)∗c для любых a, b, c∈  .
.
2) в  существует нейтральный элемент относительно операции «∗», т. е. ∃e∈
существует нейтральный элемент относительно операции «∗», т. е. ∃e∈  : a∗e=e∗a=a, для любого a∈
: a∗e=e∗a=a, для любого a∈  .
.
3) в  для любого элемента существует симметричный ему элемент, т. е. для любого a∈
для любого элемента существует симметричный ему элемент, т. е. для любого a∈  ∃a'∈
∃a'∈  : a∗a'=a'∗a=e.
: a∗a'=a'∗a=e.
Определение 20. Группа  относительно операции «∗» называется абелевой, если операция «∗» коммутативна на
относительно операции «∗» называется абелевой, если операция «∗» коммутативна на  , то есть a∗b=b∗a для любых a, b∈
, то есть a∗b=b∗a для любых a, b∈  .
.
Определение 21. Группа относительно операции умножения называется мультипликативной.
Определение 22. Если  – конечное множество, являющееся группой, то
– конечное множество, являющееся группой, то  называется конечной группой, а число
называется конечной группой, а число 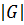 элементов в
элементов в  – порядком группы
– порядком группы  .
.
Определение 23. Непустое подмножество 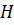 группы
группы 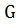 называется подгруппой группы
называется подгруппой группы  ,если
,если 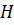 является группой относительно тех же операций, что и
является группой относительно тех же операций, что и  .
.
Обозначение: 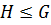 .
.
Теорема 5 (критерий подгруппы). Пусть 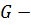 группа,
группа, 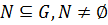 . Следовательно,
. Следовательно, 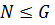 тогда и только тогда, когда
тогда и только тогда, когда
1) 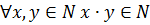 ;
;
2) 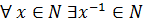 .
.
Лемма 1. Пусть 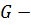 группа.
группа.
1) если 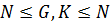 , то
, то 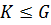 .
.
2) если 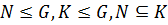 , то
, то 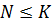 .
.
Определение 24. Пусть 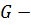 группа,
группа, 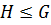 ,
, 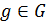 . Правым (левым) смежным классом группы
. Правым (левым) смежным классом группы  по подгруппе
по подгруппе 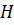 с представителем
с представителем 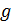 называется множество
называется множество 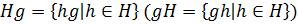 .
.
Определение 25. Пусть 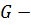 группа,
группа, 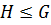 ,
, 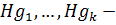 все правые смежные классы группы
все правые смежные классы группы  по подгруппе
по подгруппе 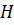 . Равенство
. Равенство 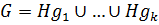 называется разложением группы
называется разложением группы  по подгруппе
по подгруппе 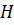 .
.
Определение 26. Число смежных классов в разложении группы  по подгруппе
по подгруппе 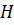 называется индексом подгруппы
называется индексом подгруппы 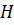 в группе
в группе  и обозначается
и обозначается 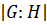 .
.
Теорема 6 (Лагранжа). Если 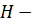 подгруппа конечной группы
подгруппа конечной группы  , то
, то
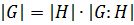 .
.
В частности, порядок конечной группы делится на порядок каждой своей подгруппы.
Лемма 2. Пусть 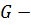 группа,
группа, 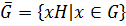 ,
, 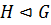 . Множество
. Множество  является мультипликативной группой относительно операции, заданной по правилу:
является мультипликативной группой относительно операции, заданной по правилу: 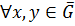
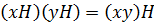 , которая называется факторгруппой группы
, которая называется факторгруппой группы  по подгруппе
по подгруппе 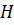 .
.
Определение 27. Группа 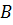 называется гомоморфным образом группы
называется гомоморфным образом группы  , если
, если 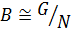 , где
, где 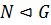 .
.
Определение 28. Подгруппа 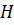 группы
группы  называется нормальной в группе
называется нормальной в группе  и обозначается
и обозначается 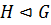 , если
, если 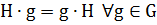 .
.
Определение 29. Группа  называется простой, если она не имеет нетривиальных нормальных подгрупп.
называется простой, если она не имеет нетривиальных нормальных подгрупп.
Определение 30. Пусть 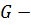 группа,
группа, 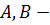 ее подгруппы. Произведение
ее подгруппы. Произведение 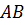 определяется как множество элементов
определяется как множество элементов 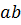 , где
, где 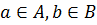 . Если
. Если 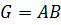 , то говорят, что группа
, то говорят, что группа  является произведением своих подгрупп
является произведением своих подгрупп 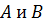 .
.
Теорема 7. Пусть 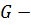 группа,
группа, 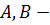 ее подгруппы.
ее подгруппы. 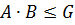 тогда и только тогда, когда
тогда и только тогда, когда 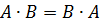 .
.
Теорема 8. Пусть 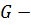 группа,
группа, 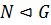 . Тогда
. Тогда
1) если 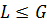 , то
, то 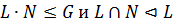 ;
;
2) если 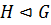 , то
, то 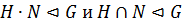 .
.
Определение 31. Группа  называется внутренним прямым произведением своих подгрупп
называется внутренним прямым произведением своих подгрупп 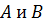 , если:
, если:
1) 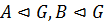 ;
;
2) 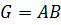 ;
;
3) 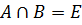 .
.
Определение 32. Наименьшее натуральное число 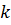 , при котором
, при котором
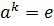 , называют порядком элемента
, называют порядком элемента 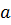 и обозначают
и обозначают 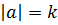 .
.
Определение 33. Элемент 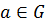 называется
называется 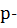 элементом, если
элементом, если 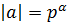 ,
, 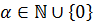 .
.
Определение 34. Группа 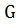 называется
называется 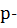 группой, если всякий ее элемент является
группой, если всякий ее элемент является 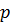 - элементом.
- элементом.
Определение 35. Силовской 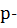 подгруппой конечной группы
подгруппой конечной группы  называют такую
называют такую 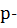 подгруппу, индекс которой не делится на
подгруппу, индекс которой не делится на 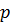 .
.
Определение 36. Группа  называется нильпотентной, если все ее силовские подгруппы нормальны.
называется нильпотентной, если все ее силовские подгруппы нормальны.
Лемма 3. Нильпотентная группа является прямым произведением своих силовских подгрупп.
Лемма 4. 1) Подгруппа и факторгруппа нильпотентной группы нильпотентны.
2) Прямое произведение нильпотентных групп является нильпотентной группой.
Определение 37. Пусть 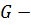 группа. Цепью подгрупп называется последовательность подгрупп
группа. Цепью подгрупп называется последовательность подгрупп 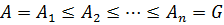 , соединяющих подгруппы
, соединяющих подгруппы 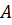 и
и  .
.
Определение 38. Пусть 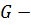 группа. Цепь подгрупп вида
группа. Цепь подгрупп вида  называется рядом группы
называется рядом группы  .
.
Определение 39. Ряд 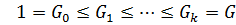 группы
группы  называется 1) субнормальным, если
называется 1) субнормальным, если 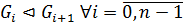 ;
;
3) нормальным, если 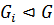
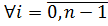 .
.
Определение 40. Пусть  - субнормальный ряд конечной группы
- субнормальный ряд конечной группы  (
( 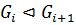 ). Факторгруппа
). Факторгруппа 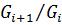 называется фактором группы
называется фактором группы  .
.
Определение 41. Субнормальный ряд  группы
группы  , не допускающий уплотнения без повторения членов ряда, называется композиционным рядом.
, не допускающий уплотнения без повторения членов ряда, называется композиционным рядом.
Определение 42. Нормальный ряд  группы
группы  , не допускающий уплотнения без повторения членов ряда, называется главным рядом.
, не допускающий уплотнения без повторения членов ряда, называется главным рядом.
Определение 43. Факторы композиционного ряда называются композиционными факторами.
Факторы главного ряда называются главными факторами.
Определение 44. Подгруппа 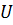 называется субнормальной подгруппой группы
называется субнормальной подгруппой группы  , если существуют подгруппы
, если существуют подгруппы 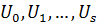 такие, что
такие, что 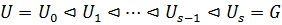 .
.
Запись 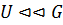 означает, что
означает, что 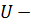 субнормальная подгруппа группы
субнормальная подгруппа группы  .
.
Определение 45. Группа  называется расширением
называется расширением 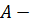 группы с помощью
группы с помощью 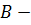 группы, если
группы, если 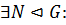
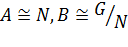 .
.
Определение 46. Пусть 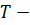 подмножество группы
подмножество группы  . Пересечение всех подгрупп группы
. Пересечение всех подгрупп группы  , содержащих подмножество
, содержащих подмножество 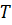 , называется подгруппой, порожденной подмножеством
, называется подгруппой, порожденной подмножеством 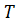 , и обозначается
, и обозначается 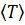 .
.
Теорема 9 (о соответствии). Пусть 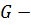 группа,
группа, 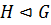 . Тогда
. Тогда
1) если 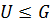 и
и 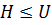 , то
, то 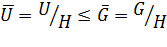 ;
;
2) каждая подгруппа факторгруппы 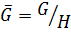 имеет вид
имеет вид 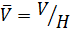 , где
, где 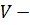 подгруппа группы
подгруппа группы  и
и 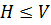 ;
;
3) отображение 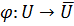 является биекцией множества
является биекцией множества 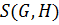 на множество
на множество 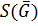 , где
, где 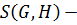 совокупность всех подгрупп группы
совокупность всех подгрупп группы  , содержащих подгруппу
, содержащих подгруппу 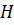 ;
; 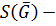 совокупность всех подгрупп группы
совокупность всех подгрупп группы 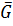 ;
;
4) если 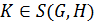 , то
, то 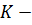 нормальная подгруппа группы
нормальная подгруппа группы  тогда и только тогда, когда
тогда и только тогда, когда 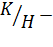 нормальная подгруппа факторгруппы
нормальная подгруппа факторгруппы 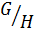 .
.
Определение 47. Группа  называется комонолитической, если она содержит единственную максимальную нормальную подгруппу (комонолит).
называется комонолитической, если она содержит единственную максимальную нормальную подгруппу (комонолит).
Определение 48. Нормальная подгруппа 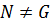 группы
группы  называется максимальной нормальной подгруппой группы
называется максимальной нормальной подгруппой группы  , если
, если 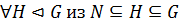 следует, что
следует, что 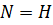 или
или 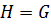 .
.
Элементы теории классов групп.
Определение 49. Классом групп называется всякое множество групп, которое вместе с каждой своей группой  содержит и все группы, изоморфные ей.
содержит и все группы, изоморфные ей.
Если группа (подгруппа)  принадлежит классу групп
принадлежит классу групп 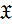 , то
, то  называют
называют 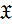 - группой (подгруппой).
- группой (подгруппой).
Определение 50. Операцией на классах групп называется отображение 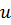 множества классов групп в себя.
множества классов групп в себя.
Произведение операций определяется следующим образом:
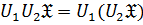 . И вообще:
. И вообще: 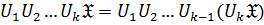 .
.
Рассмотрим следующие операции на классах групп:
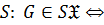 когда
когда  является подгруппой некоторой
является подгруппой некоторой 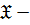 группы, то есть
группы, то есть 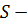 отображение, которое ставит в соответствие классу групп
отображение, которое ставит в соответствие классу групп 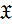 класс групп, состоящий из всех подгрупп всех
класс групп, состоящий из всех подгрупп всех 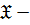 групп;
групп;
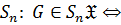 когда
когда  является нормальной подгруппой
является нормальной подгруппой 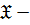 группы;
группы;
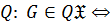 когда
когда  является гомоморфным образом некоторой
является гомоморфным образом некоторой 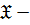 группы;
группы;
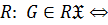 когда
когда  является произведением конечного числа своих нормальных
является произведением конечного числа своих нормальных 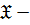 подгрупп;
подгрупп;
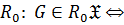 когда
когда  является прямым произведением своих нормальных
является прямым произведением своих нормальных 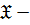 подгрупп;
подгрупп;
Определение 51. Класс групп 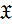 называется замкнутым относительно операции
называется замкнутым относительно операции 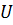 или
или 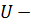 замкнутым, если
замкнутым, если 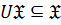 .
.
Определение 52. Класс групп 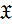 называется:
называется:
1) 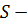 замкнутым или наследственным, если
замкнутым или наследственным, если 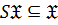 , то есть
, то есть 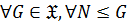 всегда
всегда 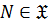 ;
;
2) 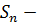 замкнутым или нормально наследственным, если
замкнутым или нормально наследственным, если 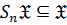 , то есть
, то есть 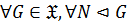 всегда
всегда 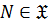 ;
;
3) 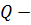 замкнутым или гомоморфом, если
замкнутым или гомоморфом, если 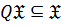 , то есть
, то есть 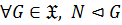 всегда
всегда 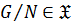 ;
;
4) 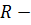 замкнутым, если
замкнутым, если 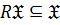 , то есть если
, то есть если 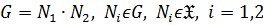 , то
, то 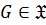 ;
;
5) 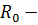 замкнутым, если
замкнутым, если 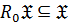 , то есть если
, то есть если 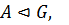
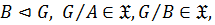 то
то 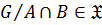 .
.
Лемма 5. Для произвольного класса групп 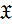 справедливо:
справедливо:
1) 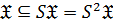 , то есть
, то есть 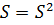 ;
;
2) 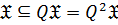 , то есть
, то есть 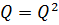 ;
;
3) 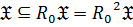 , то есть
, то есть 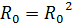 ;
;
4) 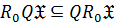 ;
;
5) 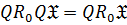 .
.
Теорема 9. Если класс 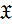 замкнут относительно произведений нормальных
замкнут относительно произведений нормальных 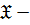 подгрупп, то каждая субнормальная
подгрупп, то каждая субнормальная 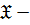 подгруппа группы
подгруппа группы  содержится в некоторой нормальной
содержится в некоторой нормальной 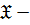 подгруппе группы
подгруппе группы  .
.
Следствие 1. Пусть класс 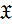 замкнут относительно произведений нормальных
замкнут относительно произведений нормальных 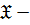 подгрупп. Если
подгрупп. Если 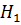 и
и 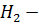 субнормальные
субнормальные 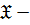 подгруппы группы
подгруппы группы  , то
, то 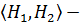 субнормальная
субнормальная 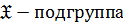 .
.
