Модульна контрольна робота № 4
Розширення поняття числа. Елементи алгебри. Величини та одиниці їх вимірювання
Варіант 1
1. Розв’яжіть рівняння 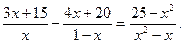
2. Розв’яжіть нерівність 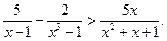
3. Побудуйте графік функції 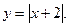
4. Знайдіть область визначення функції 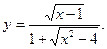
5. Площі двох прямокутників 80 см2 і 120 см2. Знаючи, що довжина і ширина
другого прямокутника на 2 см більші від довжини і ширини першого, знайти периметри цих прямокутників.
Варіант 2
1. Розв’яжіть рівняння 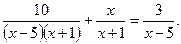
2. Розв’яжіть нерівність 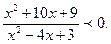
3. Побудуйте графік функції 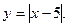
4. Знайдіть область визначення функції 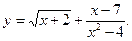
5. З дерев’яного бруска, який має форму прямокутного паралелепіпеда, довжина якого 24 см, ширина в 3 рази менша за довжину, а висота 11 см, вирізали куб з ребром 6 см. Знайти об’єм частини, яка залишилася.
Варіант 3
1. Розв’яжіть рівняння 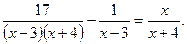
2. Розв’яжіть нерівність 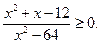
3. Побудуйте графік функції 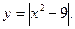
4. Знайдіть область визначення функції 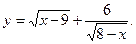
5.Одне ребро прямокутного паралелепіпеда дорівнює 44 см, друге – на 25% довше, ніж третє. Об’єм прямокутного паралелепіпеда дорівнює 22 000 см3.
Знайдіть площу кожної грані.
Варіант 4
1. Розв’яжіть рівняння 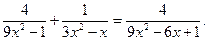
2. Розв’яжіть нерівність 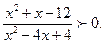
3. Побудуйте графік функції 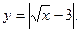
4. Знайдіть область визначення функції 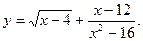
5. За три дні турист проїхав 3220км. За перший день він проїхав одну четверту всього шляху, за другий день 1920 км, а за третій день – решту шляху. Скільки кілометрів проїхав турист за третій день?
Додаток 3
Тематичний план курсу
теоретичні основи математики
(спеціальність 5. 01010201 Початкова освіта)
| Розділи, теми | Загальний обсяг | Всього аудиторних | З них | Самостійна робота студента. | |||
| Лекції | Практичних | Семінар. | |||||
| Модуль 1 Висловлення і предикати. Множини, відповідності, відношення. 1.1. Математичні поняття та їх означення. 1. 2 .Елементи математичної логіки. Структура і види теорем 1. 3. Текстова задача. 1. 4. Множини і операції над ними. 1. 5. Відношення і відповідність. | |||||||
| Модуль 2 Цілі невід’ємні числа. Додавання і віднімання, множення і ділення цілих невід’ємних чисел 2.1. Десяткова система числення. 2. 2. Теоретико – множинний підхід до побудови арифметики цілих невід’ємних чисел (для суми і різниці). 2. 3. Теоретико – множинний підхід до побудови арифметики цілих невід’ємних чисел (для добутку і частки). | |||||||
| Модуль 3 Цілі невід’ємні числа і операції над ними 3. 1. Десяткова система числення (алгоритми виконання дій). 3. 2. Позиційні і непозиційні системи числення. 3. 3. Подільність цілих невід’ємних чисел. | |||||||
| Модуль 4 Розширення поняття числа. Елементи алгебри та геометрії. Величини, одиниці їх вимірювання 4.1. Раціональні числа, дії над ними, їх властивості. Дійсні числа і дії над ними. 4.2. Математичні вирази, рівності і нерівності. Рівняння та їх властивості. 4.3. Функції, графіки і їх властивості. 4.4. Поняття величини і її вимірювання. Довжина відрізка, її властивості і вимірювання. Площа фігури і її вимірювання. Об’єм тіла і його вимірювання. Маса тіла і її вимірювання. Час і його вимірювання. Вартість та залежність між величинами ціна, кількість, вартість. | |||||||
| Всього годин у відповідності з навчальним планом. | |||||||
Форма підсумкового контролю - екзамен.
Додаток 4
Критерії оцінювання успішності студентів
з дисципліни «Теоретичні основи математики»
У ході вивчення курсу „Теоретичні основи математики" здійснюється поточний та підсумковий контроль знань студентів. Оцінювання знань студентів відбувається за рейтинговою системою.
Об'єктом поточного контролю є систематичність і якість роботи студентів під час практичних занять, а також виконання завдань модульного контролю.
За кожне практичне заняття, залежно від якості підготовки і активності, студент може отримати за перший модуль від 0 до 5 балів, за другий модуль від 0 до 10 балів, за третій модуль – від 0 до 5 балів, за четвертий модуль – від 0 до 10 балів.
Модульний контроль оцінюється 15 балами за перший та другий модулі та 10 балами за третій та четвертий модулі.
Критеріями оцінювання є:
а) при усних відповідях:
- повнота розкриття питання;
- логіка викладу думки, культура мовлення;
- впевненість, емоційність, аргументованість;
- аналітичні міркування, уміння робити порівняння, висновки)
- використання при підготовці до заняття рекомендованої та додаткової
літератури (підручників, навчальних посібників, журналів та інших періодичних видань;
б) при виконанні письмових завдань (тестів, творчих робіт):
- повнота розкриття питання;
- цілісність, логічна послідовність викладу, уміння
формулювати висновки;
- охайність та грамотність оформлення письмової роботи.
Заходи з модульного контролю проводяться після завершення вивчення навчального матеріалу модуля і передбачають написання контрольної роботи.
Результати модульного контролю (поточний рейтинговий бал) складає сума балів - оцінок поточної роботи студента на практичних заняттях з модуля, модульного контролю та заохочувальних балів, які нараховуються за старанність і творчий підхід до підготовки до занять (другий та четвертий модулі).
До вивчення наступного навчального модуля допускаються студенти, які за результатами модульного контролю одержали більш ніж 60% максимально можливої суми балів.
Після завершення вивчення курсу проводиться підсумковий контроль у формі екзамену.
Підсумковий рейтинговий бал визначається як сума поточного та екзаменаційного рейтингових балів.
Облік і реєстрація показників успішності здійснюється в журналі академічної групи та в рейтинговій відомості успішності студентів. Результати складання екзамену заносяться в залікову відомість.
Система рейтингових балів для різних видів контролю:
Теоретичні основи математики
| № п/п | Вид діяльності | Коефіцієнт (вартість) виду роботи | Кількість робіт | Результат |
| ІV семестр Модуль 1 | ||||
| 1. | Практичні заняття | |||
| 2. | Модульний контроль | |||
| 3. | Модульний (поточний) рейтинговий бал | |||
| Модуль 2 | ||||
| 1. | Практичні заняття | |||
| 2. | Модульний контроль | |||
| 3. | Додаткові бали | |||
| Модульний (поточний) рейтинговий бал | ||||
| Підсумковий рейтинговий бал | ||||
| ІV семестр Модуль 3 | ||||
| 1. | Практичні заняття | |||
| 2. | Модульний контроль | |||
| 3. | Модульний (поточний) рейтинговий бал | |||
| Модуль 4 | ||||
| 1. | Практичні заняття | |||
| 2. | Модульний контроль | |||
| 3. | Додаткові бали | |||
| 4. | Модульний (поточний) рейтинговий бал | |||
| 5. | Екзамен | |||
| Підсумковий рейтинговий бал |
Схема переведення рейтингових балів у чотирибальну шкалу оцінювання
| Оцінка за чотирибальною шкалою | % максимальної суми балів |
| „відмінно" | 90 – 100 (72-80) |
| „добре" | 70-89 (56-71) |
| „задовільно" | 60-69 (48-55) |
| „незадовільно" | 0-59 (0-47) |
Додаток 5. Робоча програма для студентів
| Модуль | Питання для самостійного опрацювання | Кількість годин | Вид навчального завдання до самостійної роботи | Форми і методи контролю | Література |
| 1. Висловлення і предикати. Множини, відповідності, відношення. (На вивчення теми відводиться всього 35 годин, на самостійну роботу – 15 годин) | 1. Підібрати означення понять та визначити їх структуру за підручниками математики для 1-4 класів. 2. Проаналізувати задачі початкового курсу математики на наявність необхідних та достатніх умов. 3. Підібрати систему задач та проаналізувати їх структуру. 4. Запропонувати задачі, які можна розв’язати різними способами та обґрунтувати більш доцільний спосіб розв’язання. 5. На кожну із розглянутих операцій над множинами підібрати конкретні приклади з підручників математики для 1-4 класів, на яких зручно було б наочно проілюструвати ці операції за допомогою діаграм Ейлера-Веннна. 6. Навести приклади класифікацій чисел та геометричних фігур, що вивчаються в початковій школі та перевірити виконання умов розбиття на класи множин, що попарно не перетинаються. 7. Навести приклади порівняння множин, встановлюючи взаємно-однозначну відповідність між їх елементами. 8. Підібрати арифметичні задачі, розв’язання яких вимагає використання теоретико-множинного змісту відношень «більше на», «менше на», «більше в», «менше в». | 1 год 2год 2 год 2 год 2год 2 год 2 год 2 год | Робота з підручником, самостійне вивчення питання і конспектування. Робота з підручниками Математика 1 – 4 класи. Самостійне вивчення питань із розробкою конспекту. Робота з підручниками Математика 1 – 4 класи. Підготовка письмових відповідей на питання. Виконання підготовчої роботи до практичних занять. Робота з підручником. Самостійне вивчення питань. Підготовка письмових відповідей | Перевірка на практичному занятті Перевірка домашніх завдань Перевірка знань на практичному занятті Усна співбе-сіда (10–15 хв) Письмове опитування. Перевірка на практичному занятті. Письмове опитування Усна співбесіда Фронтальне опитування | Підручники Математика 1 – 4 класи Підручники Математика 1 – 4 класи Математика (практикум) В. М. Кухар Математика (практикум) В. М. Кухар Курс математи-ки В. Н. Боровик ТОПКМ М. В. Кухар |
| Модуль | Питання для самостійного опрацювання | Кількість годин | Вид навчального завдання до самостійної роботи | Форми і методи контролю | Література |
| 2. Цілі невід’ємні числа. Додавання і віднімання цілих невід’ємних чисел(На вивчення теми всього відво-диться 19 годин, на самостійне опрацювання – 7годин) | 1. Обґрунтувати, що кожному класу еквівалентних скінчених множин відповідає одне і тільки одне кількісне натуральне число і, навпаки, спираючись на матеріал підручника Математика 1 клас. 2. Використовуючи ілюстрації з підручника Математика 1 клас підібрати систему запитань, які доцільно поставити учням для усвідомлення ними суті аксіоми лічби і попередження помилки змішування понять кількісного і порядкового натурального числа. 3. Вказати прийоми, теоретичною основою виконання яких є властивостівіднімання числа від суми і суми від числа. 4. На знаннях якого теоретичного матеріалу базується вивчення письмового додавання та віднімання в початкових класах. | 1 година 2 години 2 години 2 години | Усна співбесіда на початку лекції з оцінкою відповідей студентів (10 хвилин) | Курс математики. В. Н. Боровик. 1995 р. с. 107 – 108, 226. ТОПКМ. В. М. Кухар. 1980. С.152 –166. | |
| Модуль 3. Цілі невід’ємні числа і операції над ними (На вивчення теми відводиться всього 27 годин, на самостійне опрацювання – 5 годин) | 1. Підібрати систему вправ, виконання яких базується на теоретико-множинному тлумаченні дій множення та ділення. 2. Обґрунтувати доцільність поетапного ускладнення вивчення випадків письмового множення і ділення в початковій школі. 3. Підібрати систему вправ, виконання яких базується на використанні алгоритмів множення та ділення. Історія виникнення десяткової та інших позиційних систем числення. 4. Скласти таблиці виконання арифметичних дій в різних системах числення. 5. Запропонувати приклади завдань з підручників з математики для початкових класів, виконання яких вимагає перевірки подільності чисел на дане число. | 1 година 1 година 1 година 1 година 1 година | Самостійне вивчення із розробкою конспекту Підготовка письмових відповідей на поставлені питання Виконання підготовчої роботи до практичних занять Написання рефератів, повідомлень | Перевірка набутих вмінь на практичних заняттях Перевірка домашніх завдань Письмове фронтальне опитування Усна співбесіда | Курс матема-тики В. М. Боровик. С. 158 Курс математики В. М. Боровик. С. 159-160. Курс математики В. М. Боровик. С. 164 –167. ТОПКМ. В. М. Кухар. С. 187. Курс математики. В. М. Боровик. С. 106 |
| Модуль 4. Розширення поняття числа. Елементи алгебри та геометрії. Величини, їх вимірювання (На вивчення теми всього відводиться 27 годин, на самостійне опрацювання – 5 годин) | 1. Короткі історичні відомості про виникнення понять раціональних чисел. Підібрати вправи, що сприятимуть формуванню поняття про додатне раціональне число та обґрунтувати доцільність їх використання в позаурочній роботі з математики. 2. Короткі історичні відомості про виникнення понять дійсних чисел. Навести приклади задач практичного характеру, що потребують розширення поняття числа. Скласти схему класифікації дійсних чисел. Підібрати завдання з використанням символіки в початковому курсі математики та поясніть їх зміст. 3. Наведіть приклади трактування в початковому курсі математики понять числової рівності і числової нерівності. За роками навчання прослідкувати послідовність введення рівнянь в початковому курсі математики та обґрунтувати доцільність такого введення. 4. Запропонувати приклади вправ з підручників математики початкових класів, під час виконання яких може бути здійснена пропедевтика поняття функції. 5. Історичні відомості про вимірювання величини. 6. Нестандартні одиниці довжини, відомості про їх походження. Підібрати вправи на знаходження площ фігур неправильної геометричної форми. Підібрати систему вправ обчислювального характеру з одиницями об’єму. Історичні відомості про одиниці вимірювання маси. Нестандартні одиниці вимірювання маси. Прилади для вимірювання часу та історія їх виникнення. Підібрати систему задач, що сприяють формуванню понять ціна, кількість і вартість. Встановити залежність між цими величинами та вказати її вид. 7. Підібрати систему завдань, що сприяють формуванню поняття про геометричні фігури та операції над ними. | 1 година 1 година | Самостійне вивчення питання. Написання рефератів, повідомлень. | Усна співбесіда з оцінкою відповідей. Перевірка домашніх завдань. | Курс математики В. Н. Боровик. С. 189. ТОПКМ. В. М. Кухар. С. 187. |
Література
I. Курс математики: Навч. Посібник В.Н.Боровик, Л.М. Вивальнюк, М.М.Мурач, О.І.Соколенко. К.: Вища шк.,1995
II. Стойлова Л.П., Пышкало А.М. « Основы начального курса математики »: Учеб. Пособие для учащихся пед. уч-щ по спец. №2001 «Преподавание в нач. классах общеобразоват. шк.»-М.: Просвещение,1988.
III. В.М. Кухар, С.І. Тадіян, В.П.Тадіян " Математика:множини, логіка, цілі числа."- Практикум: за загал. ред. Кандидата педагогічних наук В.М. Кухар.-К.: Головне видавництво видавничого об'єднання " Вища школа", 1989.
IV. В.М. Кухар, Б.М.Білий " Теоретичні основи початкового курсу математики.": Видання друге, перероблене і доповнене.-К.: Головне вид-во видавничого об'єднання " Вища шк.", 1987.
Зміст
Вступ……………………………………………………………………….3
Тема 3.1. Десяткова система числення (алгоритми виконання дій)..…5
Тема 3.2. Позиційні і непозиційні системи числення, алгоритми
виконання арифметичних дій……………………………………….….12
Практичне заняття № 1………………………………………………….19
Тема 3.3. Подільність цилих невід’ємних чисел…..…………………..23
Практичне заняття № 2…………………………………………………29
Тема 3.3. Подільність цилих невід’ємних чисел (продовження)……..31
Практичне заняття № 3…………………………………………………37
Тема 4.1. Раціональні і дійсні числа, дії над ними та їх властивості..40
Практичне заняття № 4………………………………………….……...47
Тема 4.2. Математичні вирази, рівності і нерівності. Рівняння та їх
Властивості..…………………………………………………………….50
Практичне заняття № 5……………………………………………...…57
Тема 4.3. Функції, графіки та їх властивості……………... …………61
Практичне заняття № 6…………………………………………….….76
Тема 4.4. Поняття величини та її вимірювання.....………………..…80
Практичне заняття № 7……………………………………………..…85
Додаток 1………………………………. ……………..………………94
Додаток 2………………………………………………………………95
Додаток 3………………………………………………………..……101
Додаток 4…………………………………………………………….103
Додаток 5……………………………………………………………..106
Література……………………………………………………………107
