Уравнение с учетом всех указанных факторов

Исходные данные.

Для анализа будем использовать выборку из 65 автомобилей.

Однако, прежде чем приступать непосредственно к моделированию, необходимо проверить данные и выяснить, какому закону распределения они подчиняются. Для этого можно использовать ящичковые диаграммы.

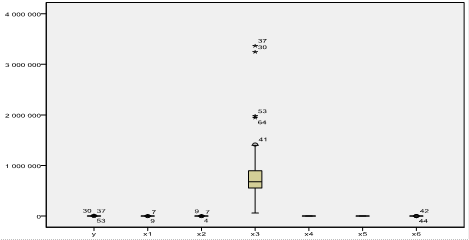
Рисунок 1 Ящеичковая диаграмма на начальных данных.

Чтобы интерпретировать полученную картинку, необходимо понимать смысл всей процедуры. Края ящичка отмечают положение 25% и 75% процентилей. рассматривать медиану как точку, делящую упорядоченную выборку пополам, а сгибы – как точки, делящие пополам полученные половинки.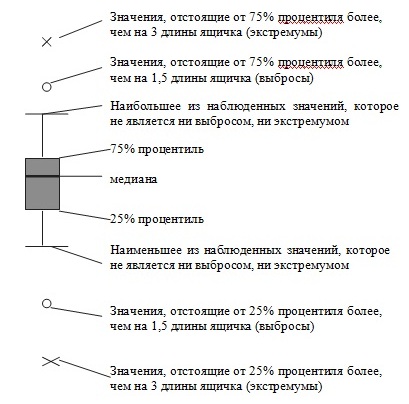

Рисунок 2 Объяснение выбросов ящичковой диаграммы

Из графика видно, что есть много аномальных значений – выбросов. Большинство выбросов приходится на фактор х3 – цена автомобиля; 5 автомобилей из 65 рассмотренных имеют чрезвычайно высокую стоимость, что может исказить последующий анализ. Необходимо исключить эти наблюдения.

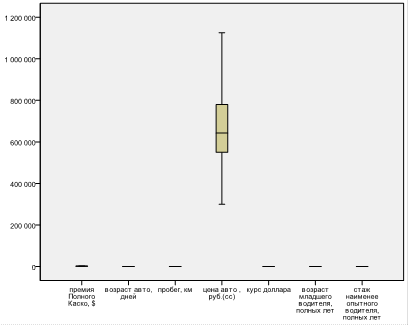
Рисунок 3 Ящичковая диаграмма. Нормированные данные.

После повторного построения диаграммы, мы видим, что теперь все факторы подчиняются нормальному закону распределения. Этот факт так же можно доказать сравнив такие описательные статистики как среднее значение (1758,6) и медиана (1681,87) – примерно одинаковы, а эксцесс (0,037) и асимметрия (0,58) не превышают по модулю 2.

После исключения выбросов, можно составить следующую таблицу для описания переменных.

Рисунок 4 Описательные статистики.

Корреляционный анализ.

Теперь проанализируем взаимосвязь признаков, оценив матрицу парных коэффициентов .

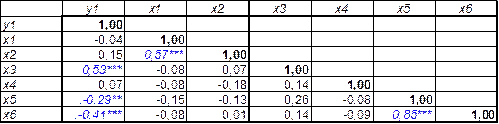
Таблица 1-корреляционная матрица

Анализ матрицы парных коэффициентов корреляции показывает, что стоимость полиса автострахования КАСКО (у) наиболее тесно связана со стоимостью машины (х₃), поскольку r (y,x₃)=0,53. Это хорошо просматривается при построении корреляционного облака. Невооруженным глазом можно заметить его овально-продолговатую форму, которая имеет положительный наклон.

Рисунок 5 Корреляционное облако.

В то же время достаточно тесная связь между факторами. Так, коэффициент корреляции между и возрастом автомобиля (х1) и пробегом x(2) равен: r₁₂ = 0,57; а между возрастом водителя и его стажем : r ₅₆ = 0,85. Учитывая тесную взаимосвязь показателей в регрессионную модель стоимости полиса КАСКО может войти лишь один показатель из пары, чтобы избежать проблемы мультиколлинеарности.

Процедуры выбора регрессоров и функциональной формы модели

Уравнение с учетом всех указанных факторов.

Рассмотрим модель в виде:

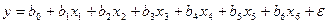
В основе модели лежат следующие гипотезы:

- Все переменные (x₁,x₂,x₃,x₄,x₅,x₆) – детерминированные величины, векторы которых независимы между собой.

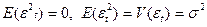- не зависят от t.

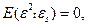- при t≠s – статистическая независимость (некоррелированность) ошибок для разных наблюдений.

- Ошибки 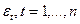имеют совместное нормальное распределение: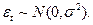

В этом случае модель называется нормальной линейной регрессией.

Результаты проведенных вычислений можно оформить в следующую таблицу для наглядности:

Таблица 2-коэффициенты регрессии (6 факторов).

Нижняя строка таблица содержит показатели адекватности модели.

Проверим, является ли построенная модель значимой. Для этого выдвинем гипотезу 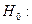полученная модель незначима. Для проверки данной гипотезы используем F-критерий:

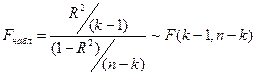=8,89 .

Можем сделать вывод о том, что уравнение регрессии значимо на уровне значимости 0,05 (т.к. F_набл 8,89 > F_крит 2,427) и переходим к анализу значимости отдельных коэффициентов регрессии.

Для уровня значимости 0,05 и числа степеней свободы 43 критическое значение t-статистики 2,016 не превосходит расчетное значение этой статистики 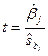только для двух факторов x(3) и x(6). Поэтому коэффициенты при остальных факторах незначимы на уровне значимости 0,05. Данный вывод так же подтверждается построением интервальной оценки для коэффициентов регрессии. Воспользуемся стандартной формулой для расчёта доверительного интервала: 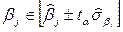, где 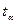рассчитывается по распределению Стьюдента на заданном уровне значимости (в нашем случае, 0,05).

b_min< b_i <b_max

-9981,9 < b₀ <17647,47

18,29 < b₁ < 5,2435725

-0,769 < b₂ < 4,078

0,0009 < b₃ <0,002

-538,43< b₄ < 358,03

-26,76 < b ₅ < 19,41

-57,22 < b ₆ < -3,024

Только два интервала не включают 0 в свои границы. Значимы коэффициенты при х₃ и х₆.

Составим прогноз для наблюдения x₀, чьи значения на 10% превышают средние значения этих показателей. Составим два прогноза: первый – без учёта случайной ошибки (прогноз среднего), второй – с учётом случайной ошибки (прогноз для случайного наблюдения).

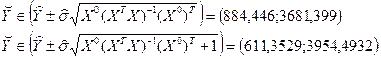
Итак, значимость уравнения в целом сопровождается незначимостью большинства коэффициентов регрессии. Поэтому полученное уравнение регрессии неприемлемо.

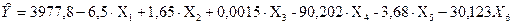
Для получения уравнения регрессии со значимыми коэффициентами используем пошаговые алгоритмы отбора факторов.

Исключение переменных.

Исключим из модели такой переменной, как возраст водителя- x(5), которой соответствует минимальное по модулю значение t-статистики |t₅|=-0,32 и для оставшихся переменных оценим уравнение регрессии с результатами в следующей таблице.

Таблица 3-коэффициенты регрессии (5 факторов)

По-прежнему на уровне значимости 0,001 значимы только коэффициенты при x (3) – цена автомобиля и x (6) – стаж наименее опытного водителя . Далее исключим из рассмотрения курс доллара - x (4), которому соответствует минимальное значение t-статистики по модулю = -0,372 и получим :

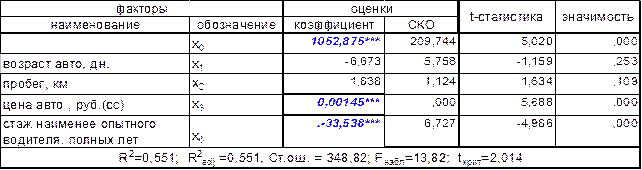
Таблица 4-коэффициент регрессии (4 фактора)

Теперь на уровне значимости 0,001 значимы не только коэффициенты при x(3) и x(5) , но и b₀ . Так же необходимо заметить, что по сравнению с предыдущими, в последней моделями увеличилось значение скорректированного коэффициента детерминации, которые показывает качество модели (используем именного этот показатель, так как он не зависит от размерности уравнении регрессии и мы можем сравнивать модели с разным количеством факторов) и снизилась стандартная ошибка. На следующем шаге исключим возраст автомобиля x(1), которому соответствует минимальное значение t-статистики = 1,159 :

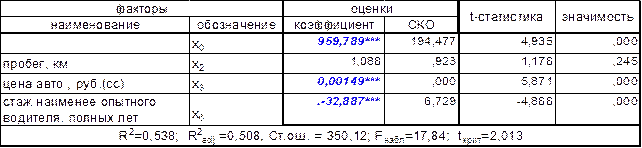
Таблица 5-коэффициенты регрессии (3 фактора)

По-прежнему имеем три коэффициента, значимых на уровне 0,001.

Исключим x(2) – пробег автомобиля, т.к. при нем b₂- это единственный незначимый коэффициент.

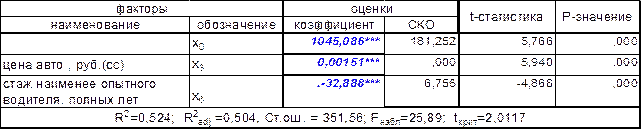
Таблица 6-коэффициент регрессии (2 фактора)

Мы получили значимое уравнение регрессии со значимыми на уровне 0,001 и интерпретируемыми коэффициентами.

Включение переменных

На первом шаге в модель цены полиса КАСКО входит переменная x(3), за которой скрывается стоимость автомобиля. Выбор падает именно на нее из-за того, что она имеет самый высокий коэффициент корреляции со стоимостью полиса автостахования : r(y, x(3))=0,53

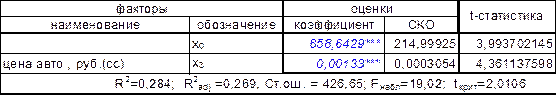
Таблица 7-коэффициенты регрессии (1 фактор)

На втором шаге, в соответствии с оценками парных коэффициентов корреляции включаем в уравнение наряду с x(3) переменные, как возраст водителя x(5) или стаж наименее опытного водителя x(6):

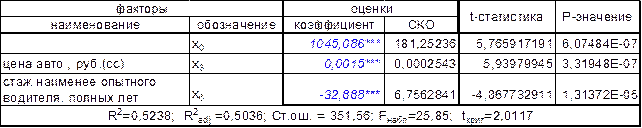
Таблица 8-коэффициенты регрессии (2 фактора – 3 и 6)

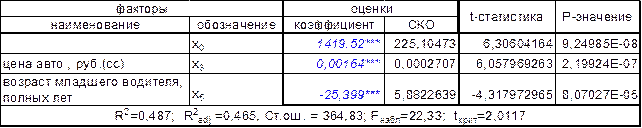
Таблица 9 коэффициенты регрессии (2 фактора – 3 и 5)

Сравнив таблицы 8 и 9, можно сделать вывод, что модель, в которой содержится стоимость автомобиля и стаж наименее опытного водителя - лучше, т.к. R²_adj больше, а стандартная ошибка – меньше.

Последующее включение переменных будет только ухудшать модель.