Реальная АЧХ не равномерна, а реальная ФЧХ не линейна, следовательно амплитудно-частотные и фазо-частотные искажения в данной цепи присутствуют!
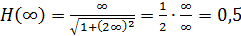
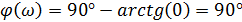
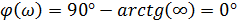
По графикам значения, полученные в п.7, эквивалентны значениям из п.4.8. Рассчитать переходную характеристику цепи h(t) и построить качественно.Из определения комплексного коэффициента передачи цепи следует, что
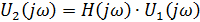
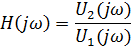
Переходимв операторную форму jω → p, получим
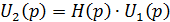
Если в качестве одного воздействия взять единичный скачок, т.е. U1(t)=1(t), то U2(t)=h(t) – переходная характеристика.
Тогда
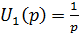 , а
, а 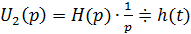 – переходная характеристика.
– переходная характеристика.
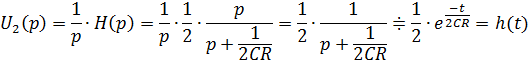
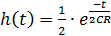 Чтобы построить качественно график переходной характеристики h(t) необходимо определить значения функции в точках 0 и ∞
Чтобы построить качественно график переходной характеристики h(t) необходимо определить значения функции в точках 0 и ∞ 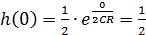
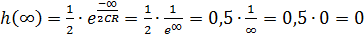 9. Рассчитать импульсную характеристику цепи hδ(t) и построить качественно.Для определения импульсной характеристики цепи используют соотношение H(jω)=
9. Рассчитать импульсную характеристику цепи hδ(t) и построить качественно.Для определения импульсной характеристики цепи используют соотношение H(jω)= 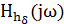 , из которого следует, что комплексный коэффициент передачи цепи – есть спектр её импульсной характеристики, т. е.
, из которого следует, что комплексный коэффициент передачи цепи – есть спектр её импульсной характеристики, т. е. 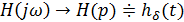
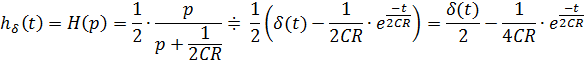
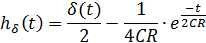
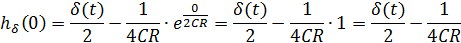
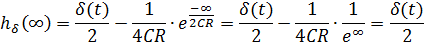
На вход электрической цепи, параметры которой рассчитаны в задаче №4, подаются сигналы:
А) Сигнал вида периодической последовательности прямоугольных видеоимпульсов напряжения с амплитудой 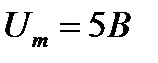 .
.
Величина скважности соответствует последней цифре номера студенческого билета: 1 2 3 4 5 6 7 8 9 0
Сважность 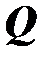 : 2 3 4 5 6 7 6 5 4 3
: 2 3 4 5 6 7 6 5 4 3
Б) Сигнал вида одиночного прямоугольного видеоимпульса,
Длительность прямоугольного импульса в микросекундах соответствует двум последним цифрам номера студенческого билета.
Задание:
1). Определить период - T заданной последовательности импульсов.
2). Рассчитать и построить амплитудный и фазовый спектры периодической последовательности прямоугольных видеоимпульсов на входе цепи. Расчету подлежат: постоянная составляющая и 5 первых гармоник спектра.
3).Построить в масштабе постоянную составляющую и 3 первых гармоники спектра этого сигнала С УЧЕТОМ ИХ АМПЛИТУД И НАЧАЛЬНЫХ ФАЗ, а также с учетом того, что спектральные составляющие имеют вид:
4). Рассчитать и построить амплитудный и фазовый спектры одиночного видеоимпульса с заданными параметрами на входе цепи.
5).Объяснить причину различий в форме входного и выходного импульса.
Решение задачи №5.
Дано:
Q=2
τи=21мкс = 21·10-6 с
U0=Um=5 В
1. Определить период - T заданной последовательности импульсов.
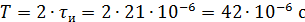
2. Рассчитать и построить амплитудный и фазовый спектры периодической последовательности прямоугольных видеоимпульсов на входе цепи. Расчету подлежат: постоянная составляющая и 5 первых гармоник спектра.
Модули:
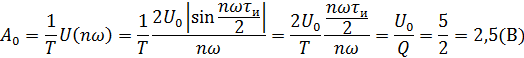
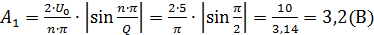 → ω
→ ω
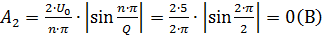 → 2ω
→ 2ω
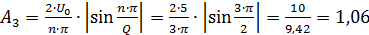 → 3ω
→ 3ω
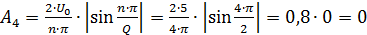 → 4ω
→ 4ω
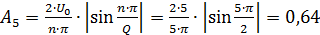 → 5ω
→ 5ω
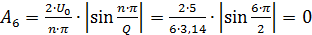 → 6ω
→ 6ω
Фаза:
Q=2, следовательно 1,2 гармоники в интервале (0; 2π/τи).
от 0 до 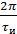
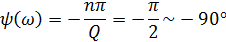
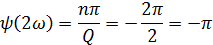
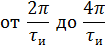
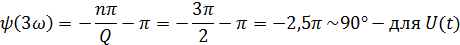
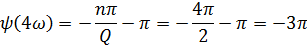
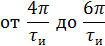
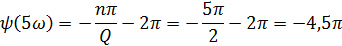
3. Построить в масштабе постоянную составляющую и 3 первых гармоники спектра этого сигнала С УЧЕТОМ ИХ АМПЛИТУД И НАЧАЛЬНЫХ ФАЗ, а также с учетом того, что спектральные составляющие имеют вид:
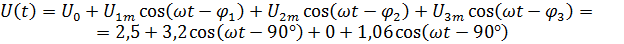
Просуммировать постоянную составляющую и 3 гармоники спектра на интервале периода первой гармоники
4. Рассчитать и построить амплитудный и фазовый спектры одиночного видеоимпульса с заданными параметрами на входе цепи.
Рассчитываем амплитудный спектр.
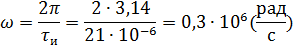
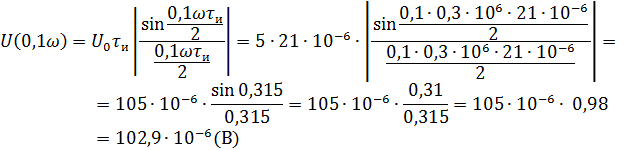
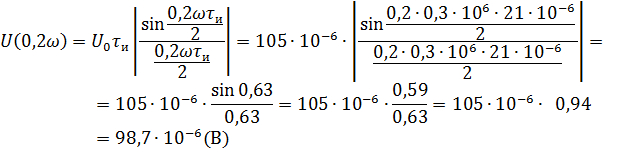
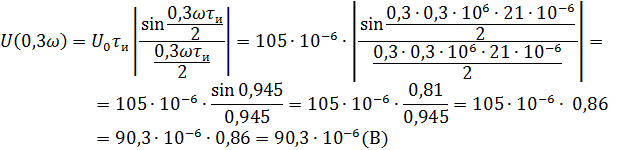
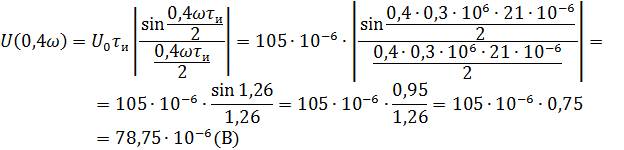
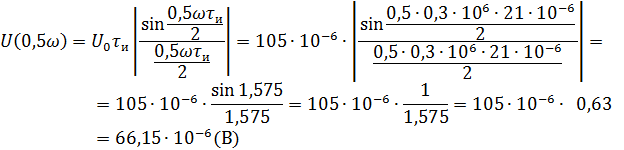
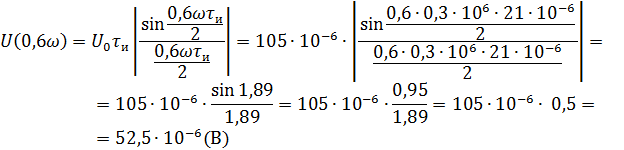
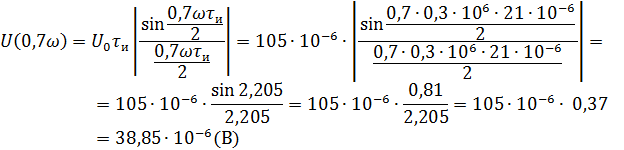
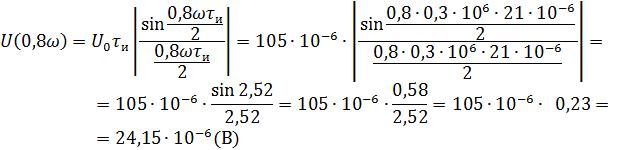
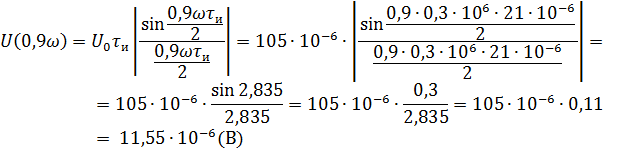
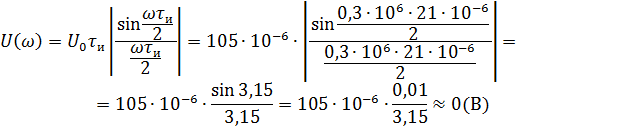
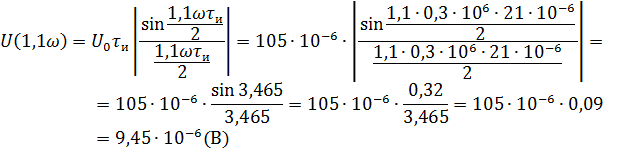
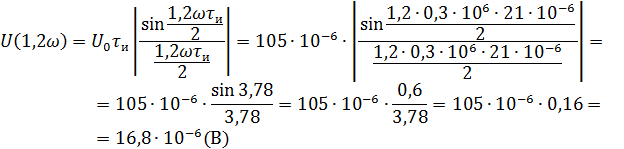
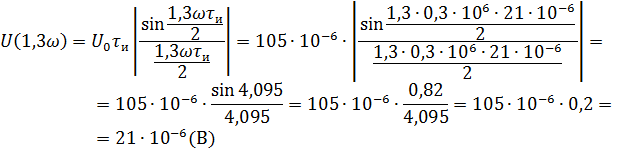
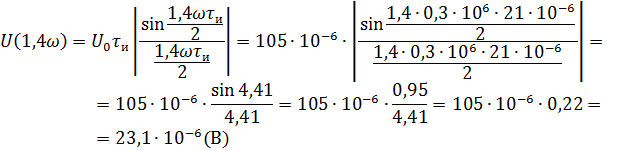
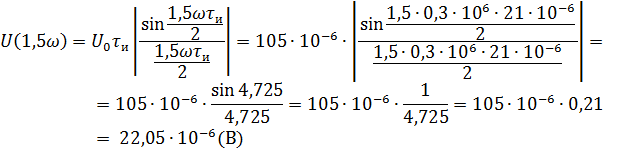
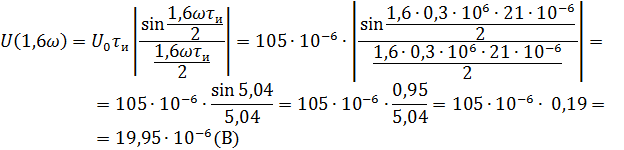
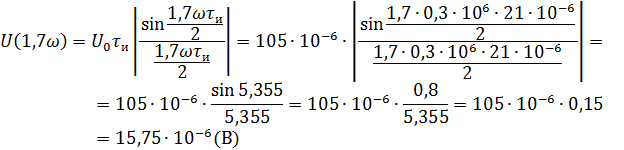
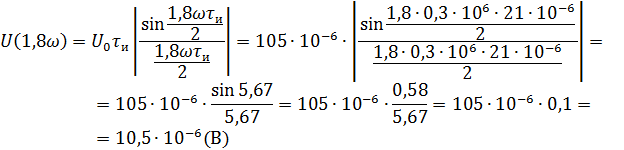
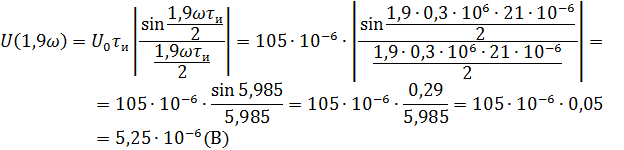
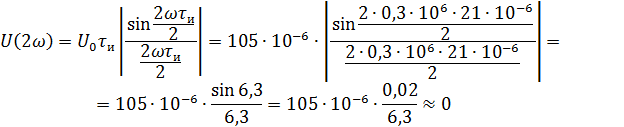
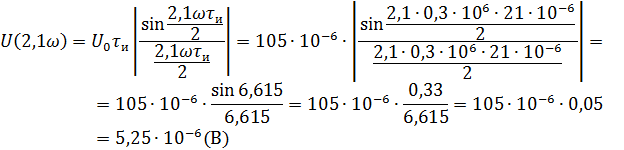
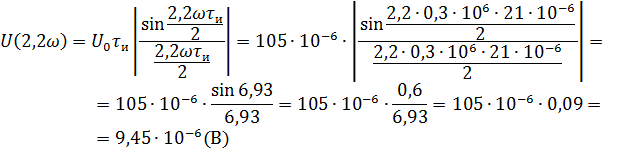
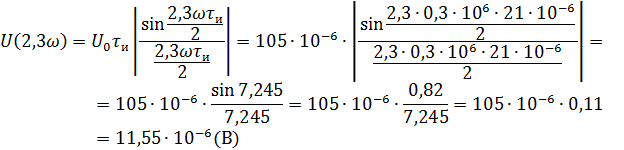
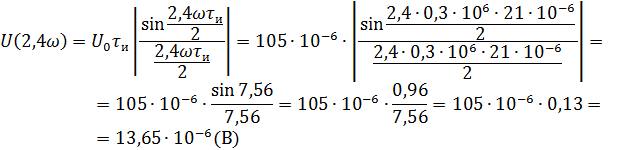
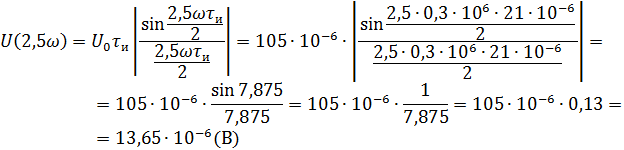
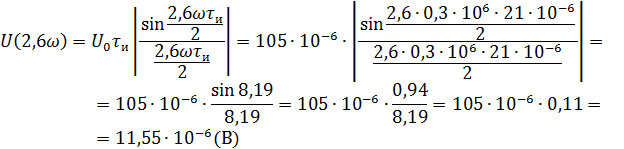
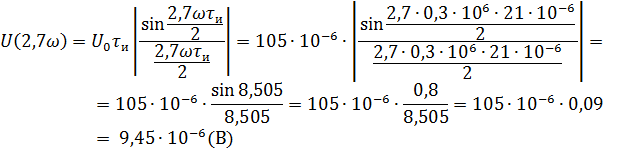
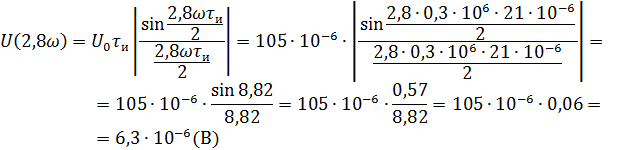
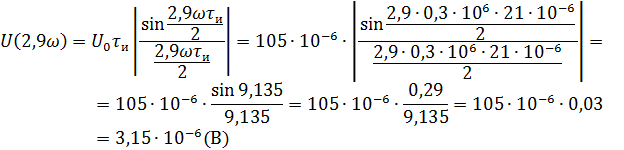
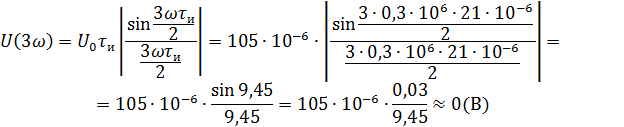
Фазовый спектр
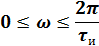
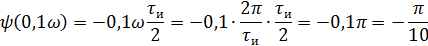
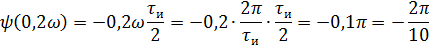
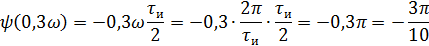
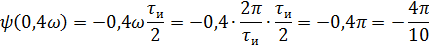
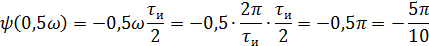
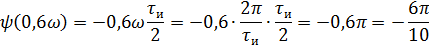
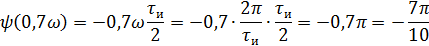
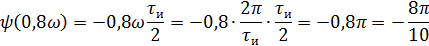
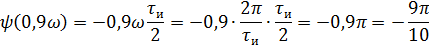
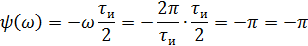
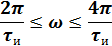
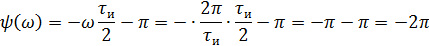
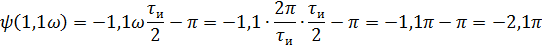
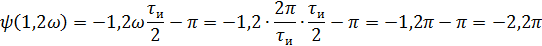
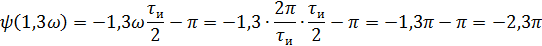
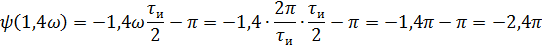
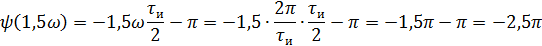
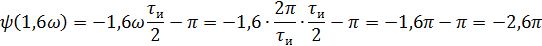
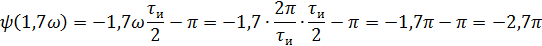
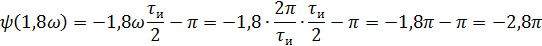
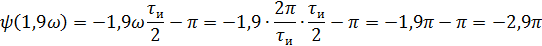
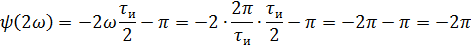
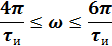
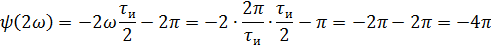
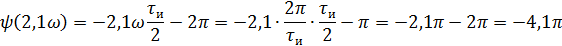
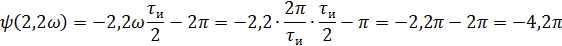
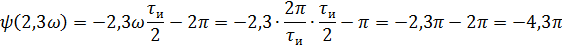
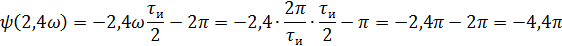
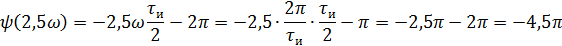
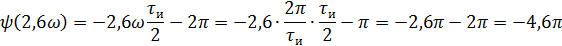
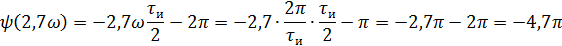
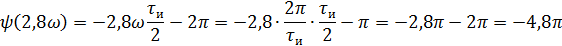
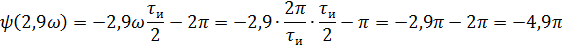
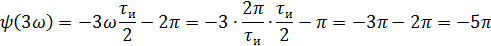
5).Объяснить причину различий в форме входного и выходного импульса.
Форма сигнала различна на входе и на выходе, так как при прохождении сигнала через линейную цепь он исказился. т.е. при прохождении через линейную систему он претерпевает фазовые и частотные искажения. Частотные искажения – АЧХ не равномерна, т.е частотные составляющие спектра входного сигнала не усиливаются/ослабляются в одно и тоже число раз. Фазовые искажения – ФЧХ не линейна, т.е. фазовый сдвиг каждой гармоники сигнала не пропорционален частоте этой гармоники.
Задача № 6. (См.учебник ОТЦ гл.8) Задан четырехполюсник – схема из задачи № 2.Требуется:1. Записать в общем виде уравнения четырехполюсника в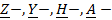 параметрах (не используя числовые данные).2. Рассчитать одну из систем параметров методом холостого хода и короткого замыкания.3. Система параметров и рабочая частота заданы в таблице 1-2.
параметрах (не используя числовые данные).2. Рассчитать одну из систем параметров методом холостого хода и короткого замыкания.3. Система параметров и рабочая частота заданы в таблице 1-2. 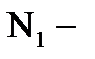 последняя цифра номера студенческого билета Таблица 1-2.
последняя цифра номера студенческого билета Таблица 1-2. 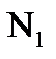 |  (МГц) (МГц) | Система параметров |
| 0 | 0,5 | 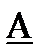 |
| 1 | 1,2 | 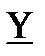 |
| 2 | 0,8 | 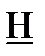 |
| 3 | 1,5 | 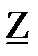 |
| 4 | 0,7 | 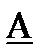 |
| 5 | 1,4 | 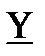 |
| 6 | 0,8 | 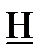 |
| 7 | 1,2 | 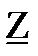 |
| 8 | 0,6 | 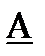 |
| 9 | 0,9 | 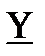 |
1. Записать в общем виде уравнение четырехполюсника в параметрах 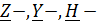 ,
, 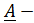 (не используя числовые данные).
(не используя числовые данные).
Схема Г-образная с Т-входом.
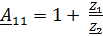
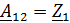
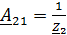
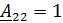
Для параметров
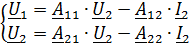
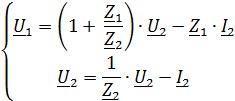
Для параметров
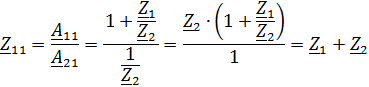
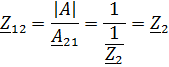
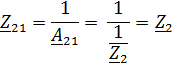
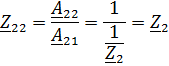
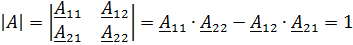
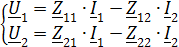
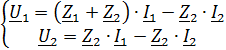
Для параметров
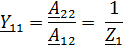
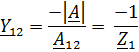
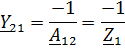
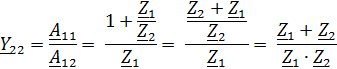
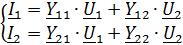
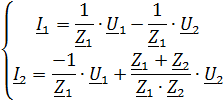
Для параметров
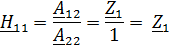
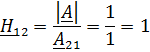
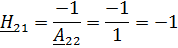
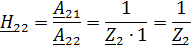
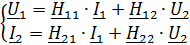
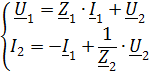
2. Рассчитать одну из систем параметров методом холостого хода и короткого замыкания.
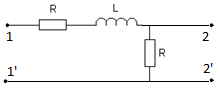 Дано:
Дано:
Y – система параметров
f=1,2МГц = 1,2 · 106 Гц
L=50мкГн=50·10-6Гн
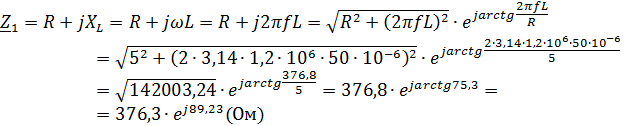
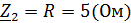
Режим короткого замыкания (при U2=0) со стороны зажимов 22’ :
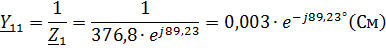
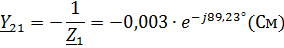
Режим короткого замыкания (при U1=0) со стороны зажимов 11’:
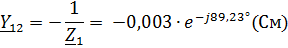
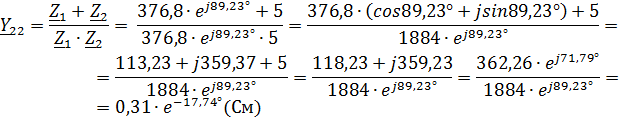
Длинная линия без потерь обладает первичными параметрами, заданными в Таблице 1.
1. Рассчитать в соответствии с данными Таблицы 1, какой минимальной длины надо взять отрезок линии, чтобы на частоте 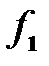 входное сопротивление линии представляло собой индуктивность L; на частоте
входное сопротивление линии представляло собой индуктивность L; на частоте 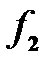 – емкость C; на частоте
– емкость C; на частоте 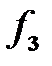 – последовательный колебательный контур в режиме резонанса напряжений; на частоте
– последовательный колебательный контур в режиме резонанса напряжений; на частоте 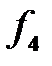 – параллельный колебательный контур в режиме резонанса токов.
– параллельный колебательный контур в режиме резонанса токов.
2. Определить, на какое сопротивление должна быть нагружена линия, чтобы в ней существовала только бегущая волна.
Таблица 1.
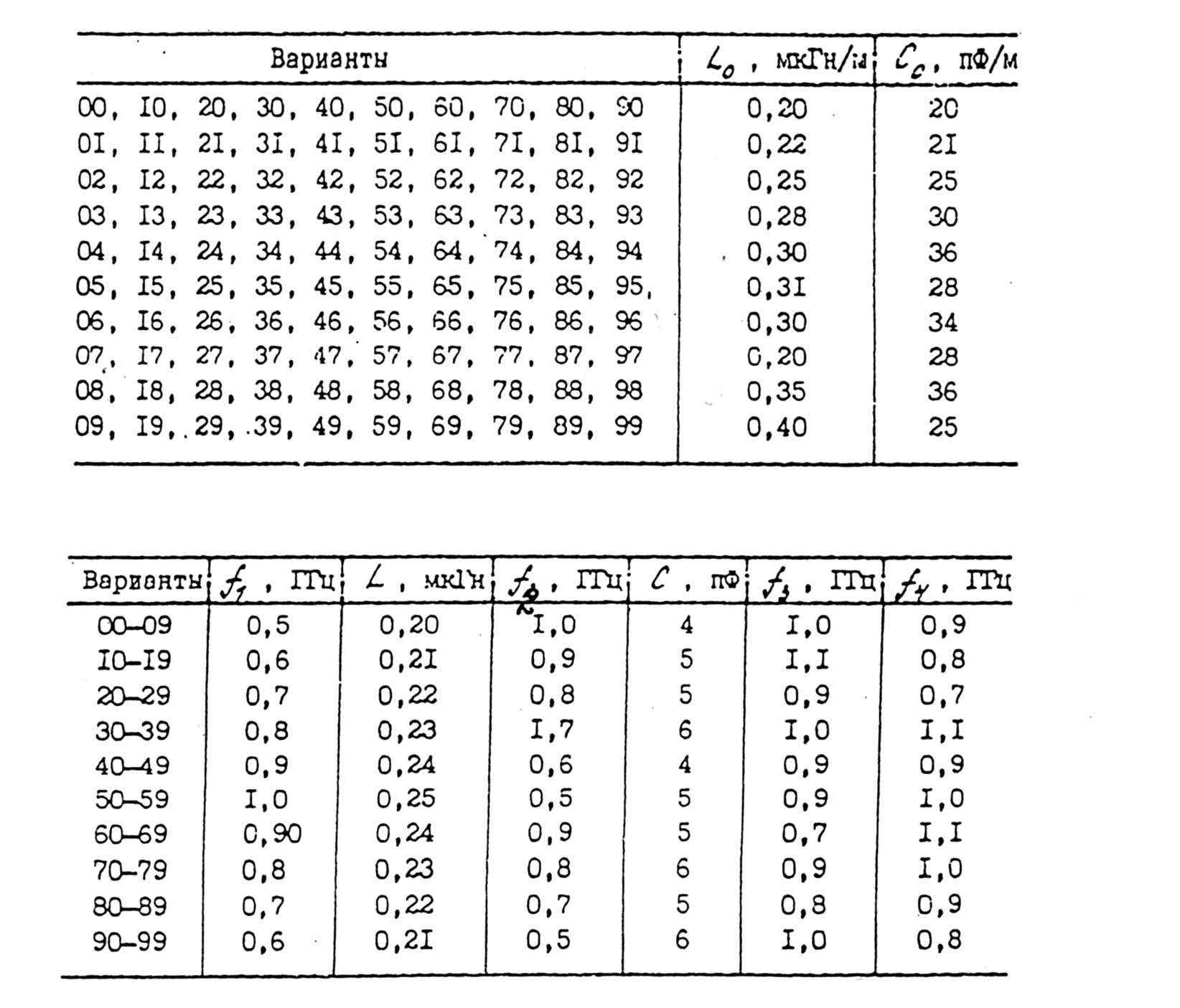
Решение задачи №7
Условия линии без потерь:
ɑ=0; R0=0; G0=0; ɣ=0; 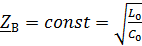
Находим волновое сопротивление линии:
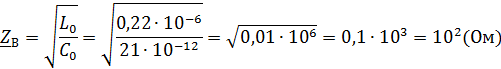
1. Какой минимальной длины надо взять отрезок линии:
1.1. чтобы на частоте 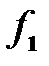 входное сопротивление линии представляло собой индуктивность L;
входное сопротивление линии представляло собой индуктивность L;
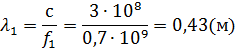
Линия короткозамкнутая
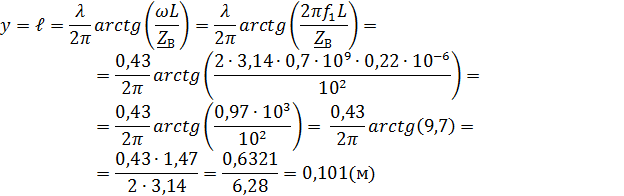
1.2. на частоте 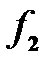 – емкость C;
– емкость C;
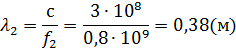
В режиме холостого хода:
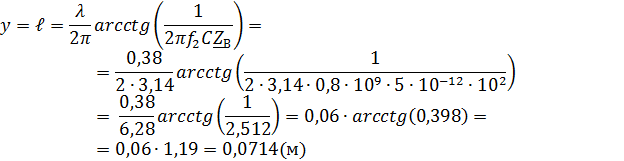
1.3. на частоте 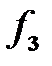 – последовательный колебательный контур в режиме резонанса напряжений;
– последовательный колебательный контур в режиме резонанса напряжений;
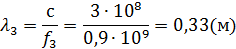
В режиме холостого хода:
1.4. на частоте 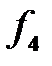 – параллельный колебательный контур в режиме резонанса токов.
– параллельный колебательный контур в режиме резонанса токов.
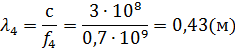
Линия короткозамкнутая
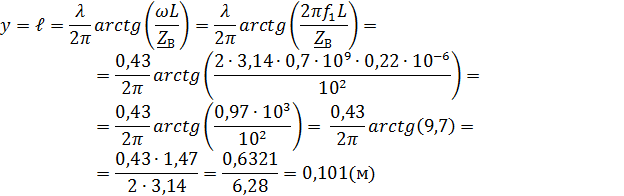
2. Определить, на какое сопротивление должна быть нагружена линия, чтобы в ней существовала только бегущая волна.
