Дифракция Фраунгофера на дифракционной решетке.

Одномерная дифракционная решетка – это система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непроз­рачными промежутками.

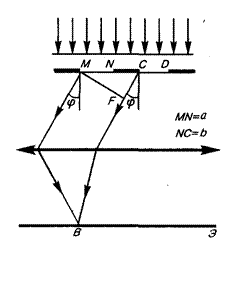Дифракционная картина на решетке определяется, как результат взаимной интерференции волн, идущих от всех щелей. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки (рис. 6). Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей D, идущих от двух соседних щелей, будут для данного направления j (j – угол дифракции) одинаковы в пределах всей дифракционной решетки:

.

Рис. 8

Кроме минимумов интенсивности, наблюдаемых от одной (каждой) щели (главные миниму­мы) и определяемых условием, рассмотренным выше:

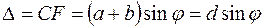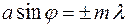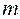( = 1, 2, 3, …),

для дифракции на решетке, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, возникнут в некоторых направлениях дополнительные минимумы. Эти дополнительные минимумы будут на­блюдаться в тех направлениях, которым соответствует разность хода лучей, исходящих, например, от крайних точек М и С соседних щелей, равная l/2, 3l/2, ..., что является условием наблюдениядополнительных минимумов:

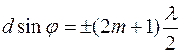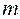( = 0, 1, 2, …) .

С другой стороны, действие одной щели будет усиливать действие другой, если

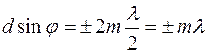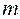( = 0, 1, 2, …),

что является условием наблюденияглавных максимумов,которое носит названиеформулы дифракционной решетки.

Тема 4. Дифракция рентгеновских лучей на кристаллах

Для наблюдения дифракционной картины необходимо, чтобы постоянная d дифракционной решетки была того же порядка, что и длина волны l падающего излучения. Для кристал­лов, являющихся естественными трехмерными пространственными дифракционными решетками, постоян­ная d порядка 10^–10 м и, следовательно, кристал­лы непригодны для наблюдения дифракции в видимом свете (l » 5×10^–7 м). Однако, дифракцию на кристаллических дифракционных решетках можно наблюдать, если в качестве падающего излучения использовать рентгеновское излучение (l » 10^–12¸10^–8 м).

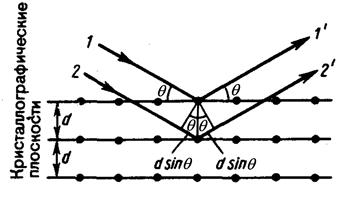Так как кристаллы это совокупность кристаллографических плоскостей (рис. 7), отстоящих друг от друга на расстоянии d, торассматривают дифракцию монохроматических рентгеновских лучей (1, 2), падающих на крис-таллы подуглом скольжения q (q – уголмежду направлением падающихлучей и кристалло-графической плоскостью).

Рис. 7Рентгеновскоеизлучениевозбуж­-

даетатомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1' и 2', интерферирующих между собой, подобно вторичным волнам, идущим от щелей дифракционной решетки. Максимумы интенсивности (дифракционные мак­симумы) наблюдаются в тех направлениях, которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлет­воряют следующему условию:

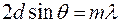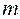( = 1, 2, 3, …),

которое носит названиеформулы Вульфа–Брэгга( 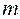– порядок спектра).

Формула Вульфа–Брэгга используется при решении двух важных задач.

1. Наблюдая дифракцию рентгеновских лучей известной длины волны l на кристал­лической структуре неизвестного строения, поворачивают кристалл и находят угол q, соответствующий дифракционным максимумам. Затем, используя формулу Вульфа–Брэгга,рассчитывают межплоскост­ное расстояния d, то есть определяют кристал­лическую структуру. Этот метод лежит в основе рентгеноструктурного анализа.

2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны l на кри­сталлической структуре с известными значениями d , измеряют угол q, соответствующий дифракционному максимуму и используют формулу Вульфа–Брэггадля расчета длины волны l падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спек­троскопии.

Глава 5. Дисперсия и поляризация света

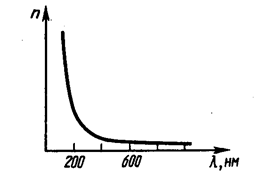Дисперсией света называется зависимость показателя преломления n вещества от частоты n (n = f (n)) или от длины волны l (n = f (l)) света (рис. 8).

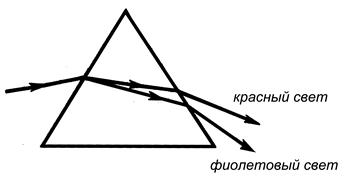
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму (рис. 9). Так как с увеличением длины волны значение показателя преломления уменьшается (рис. 8), то красные лучи отклоняются призмой слабее, чем фиолетовые (рис. 9).

Поляризация света. Согласно теории Максвелла световые волны являются поперечными: векторы напряженностей электрического 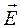и магнитного 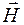полей в световой волне взаимно перпендикулярны и колеблются перпендикулярно вектору скорости 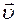распространения волны. Поэтому для описания закономерностей поляризации света рассматривают поведение лишь одного из векторов – вектора напряженности 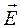электрического поля.

Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равнове­роятными ориентациями вектора 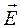. Такой свет называется естественным.Свет, в котором направление колебаний вектора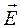каким-то образом упорядочено, называется поляризованным.Свет, в котором вектор 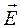колеблется только в одном направлении (перпендикулярном направлению распространения луча) называется плоскополяризованным. Плоскость, проходящая через направление колебаний вектора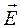плоскополяризованной волны и направление распространения этой волны, называется плоско­стью поляризации.

Естественный свет можно преобразовать в плоскополяризованный с помощью так называемых поляризаторов. В качестве поляризаторов могут быть использованы природные кристаллы, например, турмалин.

Если на пути луча поставить не одну, а две пластинки турмалина T₁ и T₂ (рис. 10) и вращать одну относительно другой вокруг направления луча, то интенсивность света, прошедшего через обе пластинки, изменяется в зависимости от угла a между оптическими осями ОО', определяющими положение плоскостей поляризации двух кристаллов-поляризаторов,по закону Малюса:

,

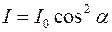где I₀ и I – соответственно интенсивности света, падающего на второй кристалл и вышедшего из него.

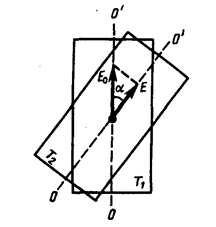
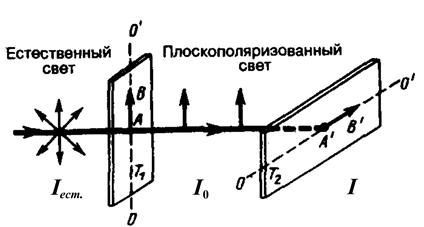Рис. 10

Пластинка Т₁ , преобразующая естественный свет в плоскополяризованный, являет­сяполяризатором. Пластинка Т₂ , служащая для анализа степени поляризации света, прошедшего поляризатор,называется анализатором.

Так как интенсив­ность естественного света, прошедшего первый поляризатор уменьшается вдвое по отношению к падающему свету на первый поляризатор, то интенсивность света, прошедшего через два поляризатора:

,

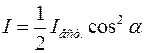откуда 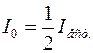для параллельных поляризаторов,

I_min = 0 для скрещенных поляризаторов ( 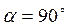).