Решение. Частота среза фильтра рад/с. После деформации частота среза будет равна

Необходимо с помощью билинейного z-преобразования определить передаточную функцию цифрового эквивалентного фильтра верхних частот. Частота дискретизации равна 150Гц, а частота среза 30Гц.

Решение. Частота среза фильтра рад/с. После деформации частота среза будет равна

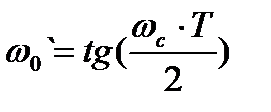
При Т=1/150Гц, 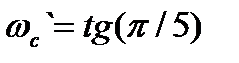=0,7265

Используя преобразование «ФНЧ» 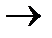«ФВЧ», получим следующую ненормированную аналоговую передаточную функцию:

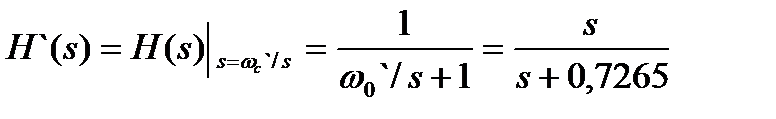
Для получения передаточной функции цифрового фильтра применим билинейное z-преобразование

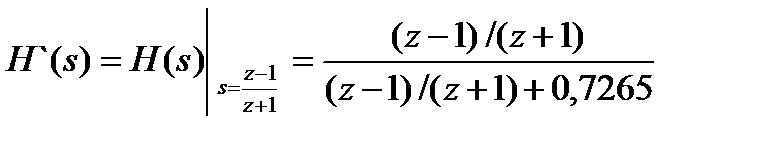
Упрощая, получим

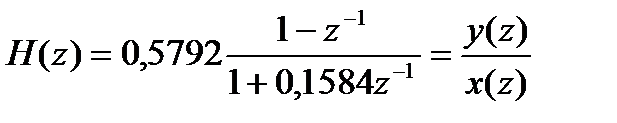
Отсюда соответствующее разностное уравнение

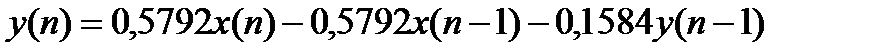
и коэффициенты фильтра:

; ;

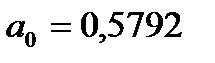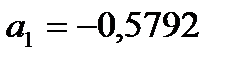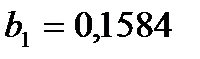
Пример. Полосовой фильтр. Необходимо получить передаточную функцию полосового фильтра Баттерворта, удовлетворяющего следующим требованиям:

Полоса пропускания – 200-300 Гц

Частота дискретизации – 2 кГц

Порядок фильтра N - 2

Решение. В качестве фильтра-прототипа возьмем аналоговый ФНЧ первого порядка (преобразование полосы частот для полосовых фильтров 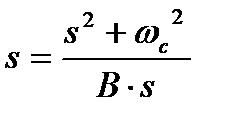удвоит порядок фильтра) со следующей(уже известной) передаточной функцией.

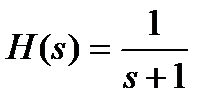
Деформированные граничные частоты полосового фильтра будут равны:

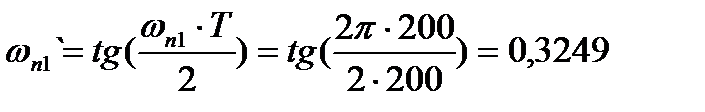
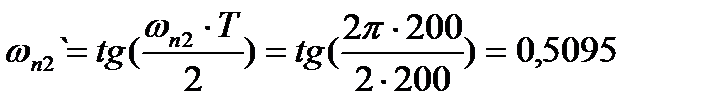
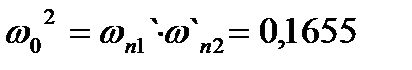
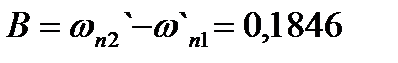
Используя преобразование «ФНЧ» «полосовой фильтр», получим

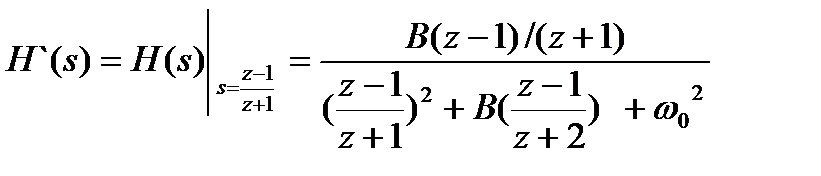
Подставляя значения 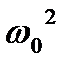и 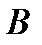, после упрощений получим

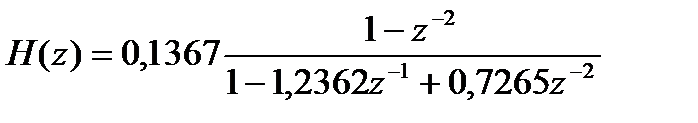
На практике БИХ- фильтры высоких порядков (например N>3), как уже отмечалось, реализуются последовательным(накладным) или параллельным соединением фильтрующих звеньев второго и/или первого порядка, что позволяет снизить влияние конечной разрядности на быстродействие фильтра. С этой целью после преобразования аналогового фильтра в дискретную форму полученную передаточную функцию H(z), если она имеет большой порядок, нужно выразить в фиксированном виде (для каскадной реализации) или как сумму членов второго и/или первого порядка (для параллельной реализации).

Следует отметить, что деформирование частотной шкалы и билинейное z-преобразование для повышения вычислительной эффективности можно объединить в одно преобразование:

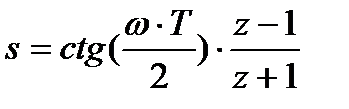
Далее, для ФНЧ и ФВЧ порядок H(z) равен порядку передаточной функции H(s) аналогового фильтра. Например, если функция H(z) получена из функции H(s) аналогового фильтра второго порядка, то и H(z) также будет описывать систему второго порядка. Для полосовых и режекторных(заградительных) фильтров порядок H(z) будет вдвое больше порядка H(s).

Кроме того, на практике иногда бывает так, что передаточную функцию H(s) существующего аналогового фильтра нужно преобразовать в функцию эквивалентного фильтра дискретного времени. В подобных ситуациях аналоговая передаточная функция реального фильтра уже дана, так что билинейное z-преобразование можно применять сразу после предварительной деформации и прямого масштабирования характеристики аналогового фильтра в характеристику цифрового фильтра.

Пример 2.10. С помощью метода взвешивания найдем коэффициенты КИХ-фильтра нижних частот, который удовлетворяет следующим требованиям:

граничная частота полосы пропускания – 1,5 кГц,

ширина переходной полосы – 0,5 кГц,

затухание в полосе подавления – > 50 дБ,

частота дискретизации – 8 кГц.

Решение. Идеальная импульсная характеристика 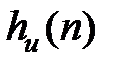для ФНЧ:

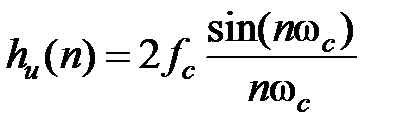, n ¹ 0,

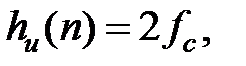n = 0,

Из таблиц, где представлены основные характеристики оконных функций, следует, что требованиям к затуханию в полосе подавления удовлетворяют функции Хемминга, Блэкмана или Кайзера. Для простоты выберем функцию Хемминга. Тогда нормированная ширина полосы перехода 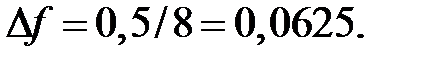Поскольку для окна Хемминга 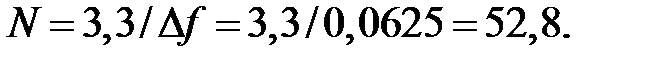Положим 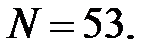Тогда коэффициенты импульсной характеристики будет равны

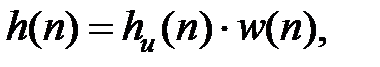
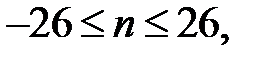
где

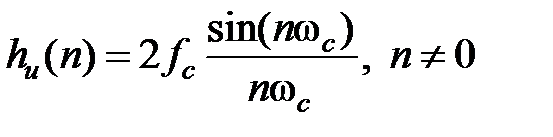
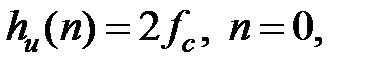
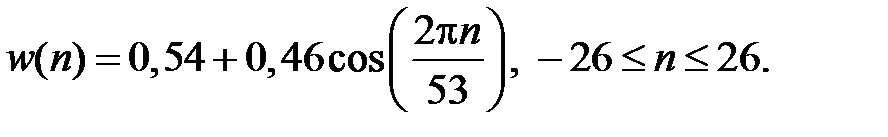
Вследствие эффекта сглаживания характеристики фильтра, вносимого весовой функцией, частота среза получающегося фильтра будет отличаться от заданной. Чтобы учесть этот эффект, используем 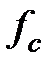– центр полосы перехода.

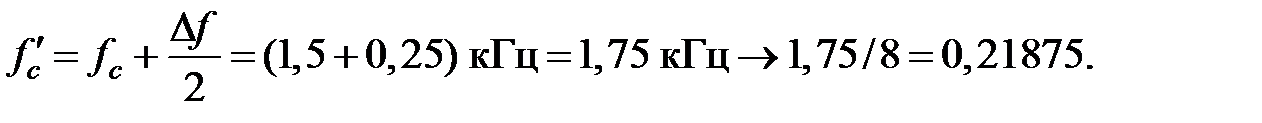
Поскольку 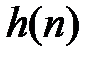– симметричная функция, можно вычислить только значение h(0), h(1), ..., h(26), а остальные можно получить из условия симметрии.

... ... ...

... ... ...
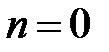
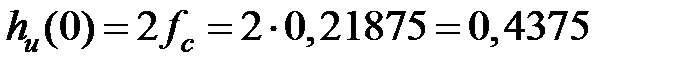
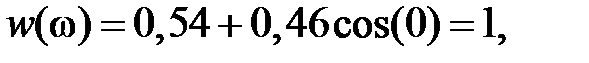
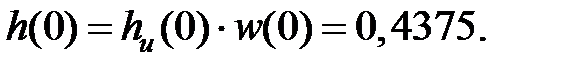
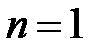
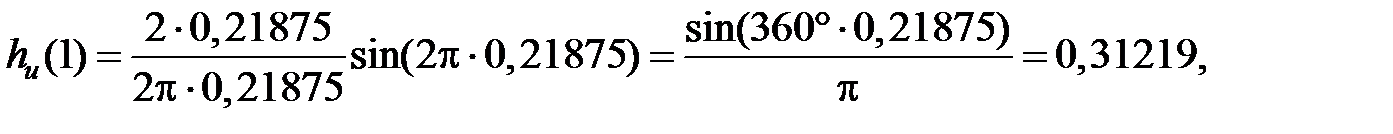
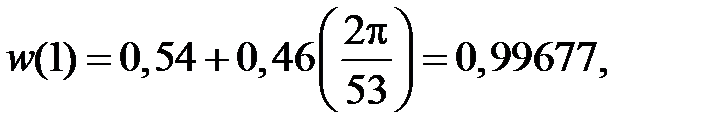
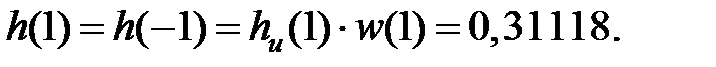
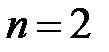
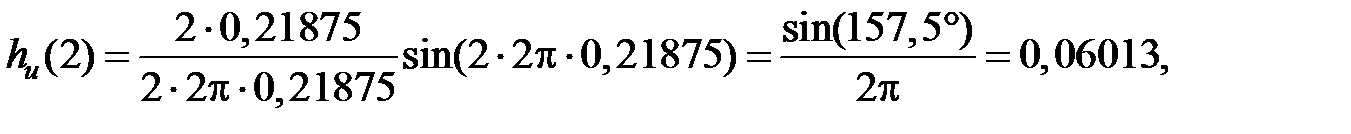
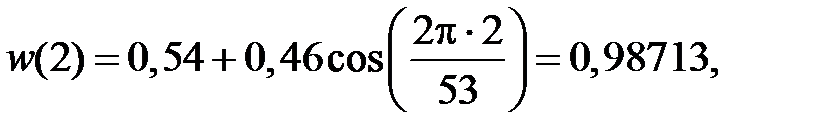
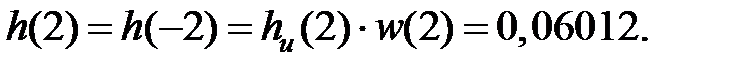