Описание структуры разбиения пространства коэффициентов на области качественно отличного динамического поведения системы

КУРСОВАЯ РАБОТА

По дисциплине: «Теория автоматического управления »

Тема: «Исследование автоматической системы»

Выполнил:

Проверил:

Согонов. С. А.

СОДЕРЖАНИЕ

1. Исходные данные
2. Описание выбранного метода исследования (достоинства, недостатки, область применения)
3. Описание структуры разбиения пространства коэффициентов на области качественно отличного динамического поведения системы.
4. Пояснение и описание всех характеристик, графиков, расчётных значений, коэффициентов, полученных в процессе выполнения задания.
5. Статическая характеристика, качество переходного процесса. Рабочая точка. Запасы устойчивости по коэффициентам системы.
6. Модель программы переходного процесса в системе.

Вывод

Исходные данные.

1.1 Структурная схема автоматической системы.

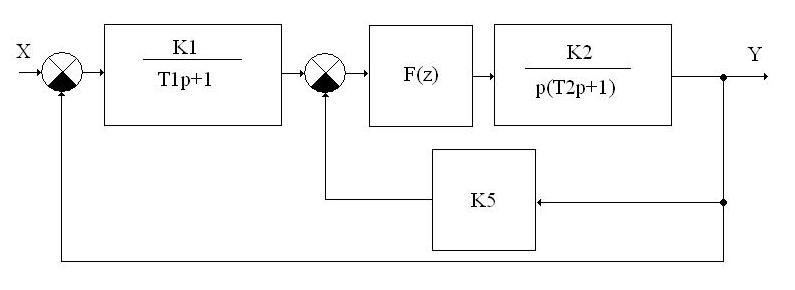
1.2 Заданная нелинейность.

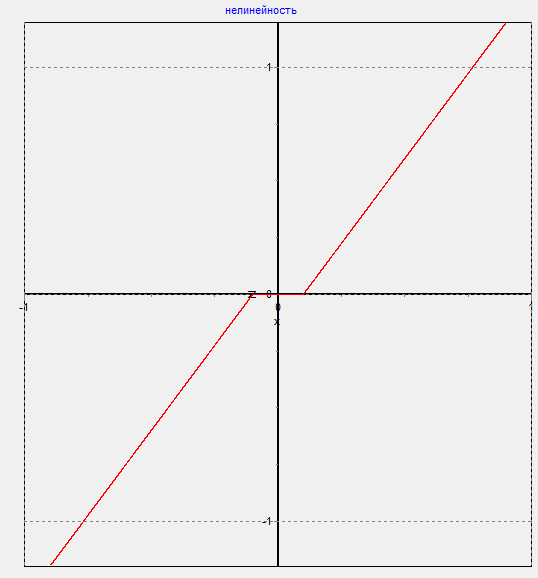
1.3 Заданные значения коэффициентов.

,

,

,

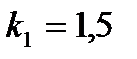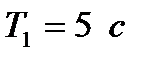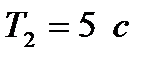a=0,1 b=0,4 с=0,45

1.4 Заданный диапазон изменения коэффициентов настройки.

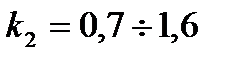, 1/c

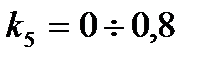
Описание метода исследования (достоинства, недостатки, область применения)

Для исследования системы применен метод гармонической баланса

(МГБ).В основе МГБлежат следующие положения: имеется нелинейное звено 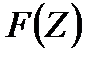, на вход которого подан гармонический сигнал 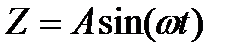.Тогда на выходе нелинейного звена будет получен периодический сигнал 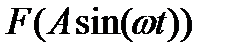. Гармоническая линеаризация получается как результат разложения выходного сигнала в ряд Фурье. Инерционность линейной части называется свойством фильтра. Чем больше инерционность тем больше свойство фильтра, тем меньше пропускаются высшие гармоники. Следовательно достаточно рассмотреть первую гармонику чтобы приблизительно оценить основные динамические свойства системы. Коэффициент гармонической линеаризации прямо пропорционален амплитуде первой гармоники и обратно пропорционален амплитуде входного сигнала.

Данный метод используется для систем выше 2-го порядка. Основным недостатком метода является то, что МГБявляется приближенным и мы не можем оценить его погрешность. В схеме нелинейное звено 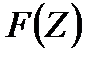заменяется на

Коэффициенты гармонической линеаризации

0, x<b

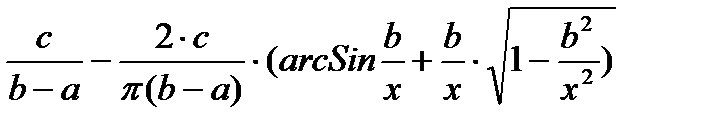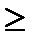q(x)= , x b

Описание структуры разбиения пространства коэффициентов на области качественно отличного динамического поведения системы.

Передаточная функция системы:

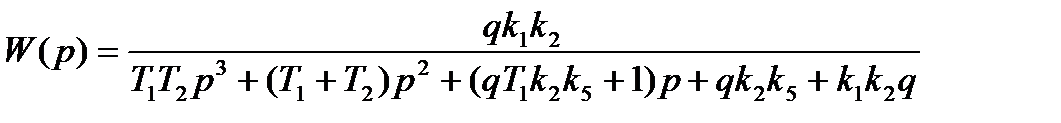
Рассмотрим характеристический полином нашей системы:

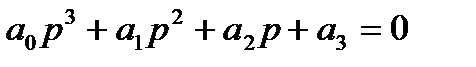
где

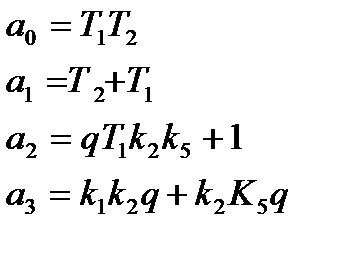
Согласно критерию Раусса-Гурвица система устойчива если

• Выполняется необходимое условие устойчивости, т. е.
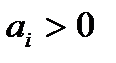
• Все диагональные миноры больше нуля

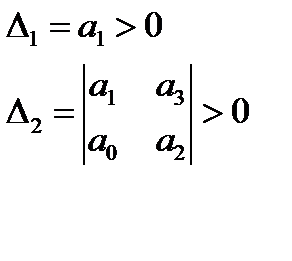
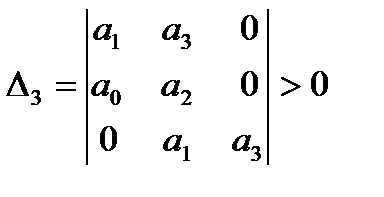
• Определитель Раусса-Гурвица больше нуля

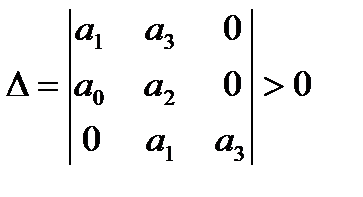
выразив g, получим

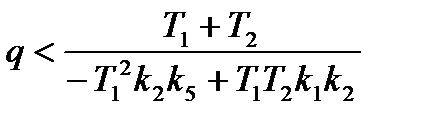
Это условие выполнено, если числитель меньше нуля

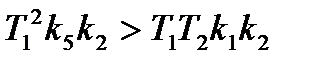
так как Т₁=Т_{2 ,} то получаем

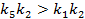
отсюда следует, что числитель будет точно меньше нуля при

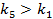
Если

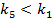
то числитель будет положительным, но неравенство будет выполняться при малых значениях k₂, значит границе устойчивости соответствует уравнение:

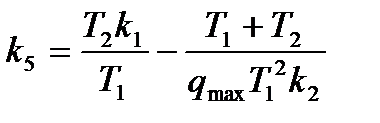
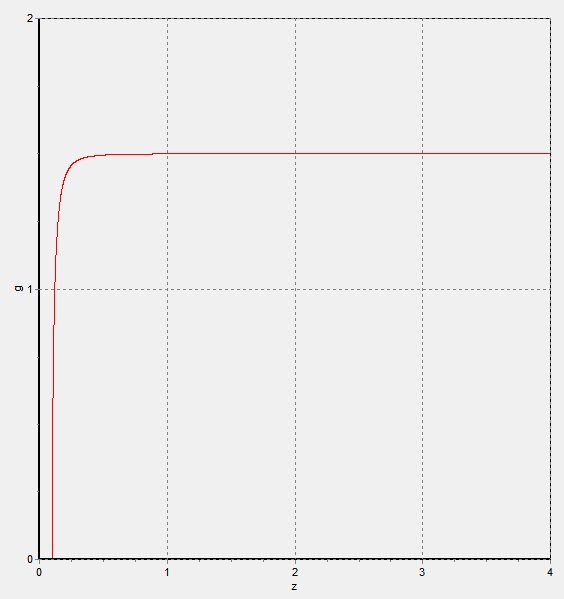
Построив графики зависимости 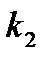от 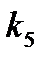, получим разбиение пространства коэффициентов 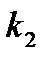и 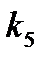на области качественно отличного динамического поведения системы. На рисунке обозначено ПЦ- область существования предельного цикла, У- область устойчивости. Область неустойчивости находиться в отрицательной области и не рассматривается.

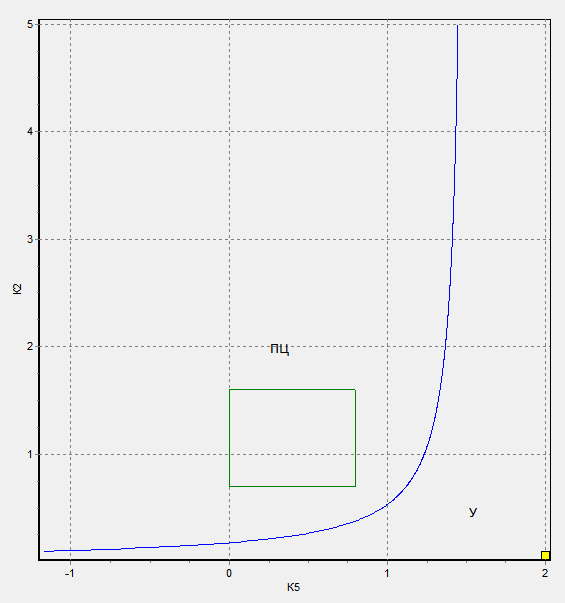
4. Пояснение и описание всех характеристик, графиков, расчётных значений, коэффициентов, полученных в процессе выполнения задания

Покажем переходную характеристику и фазовый портрет для точек, находящихся в устойчивой и области автоколебаний.

Покажем область устойчивости при данных коэффициентах:

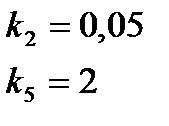
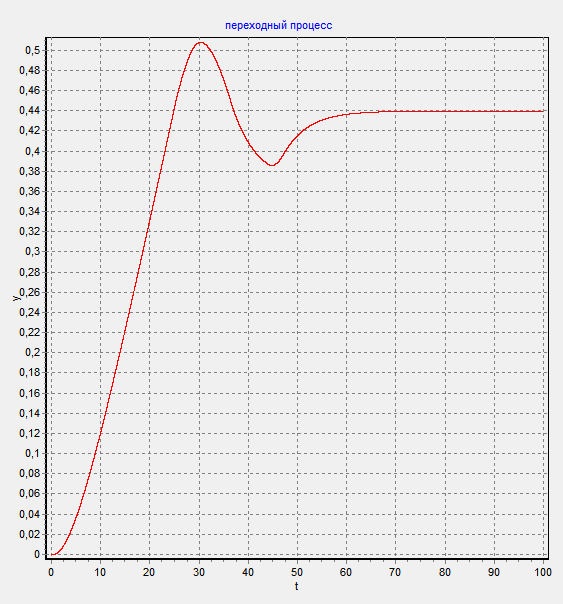
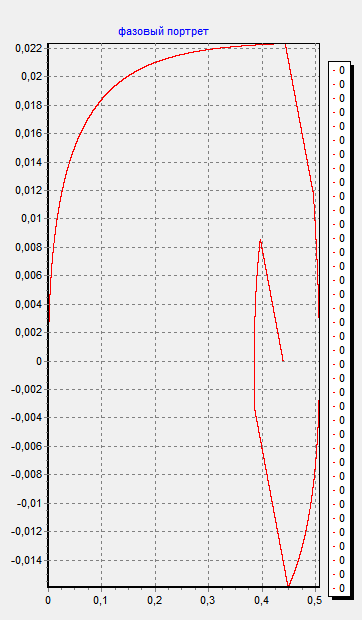
Покажем область придельного цикла при коэффициентах 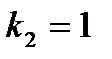, , 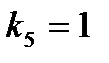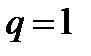при разных входных воздействиях. Аналитическое доказательство наличия придельного цикла.

Как видно из графика, при данной нелинейности существует только один придельный цикл.

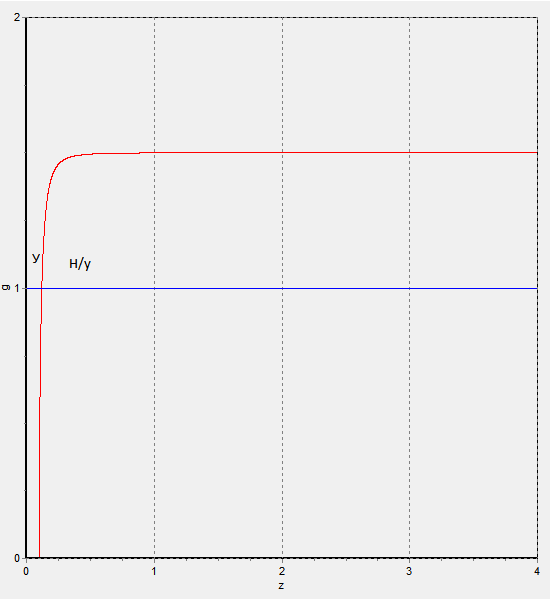
1) при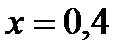

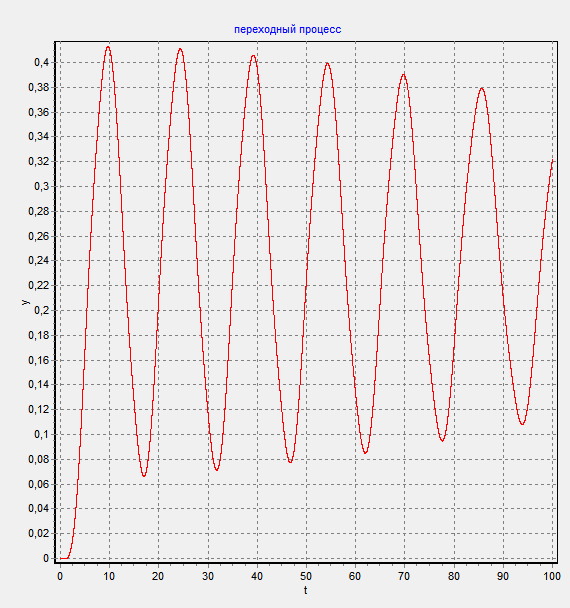
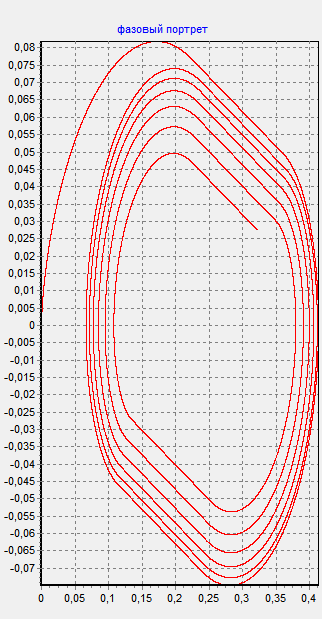
2) при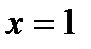

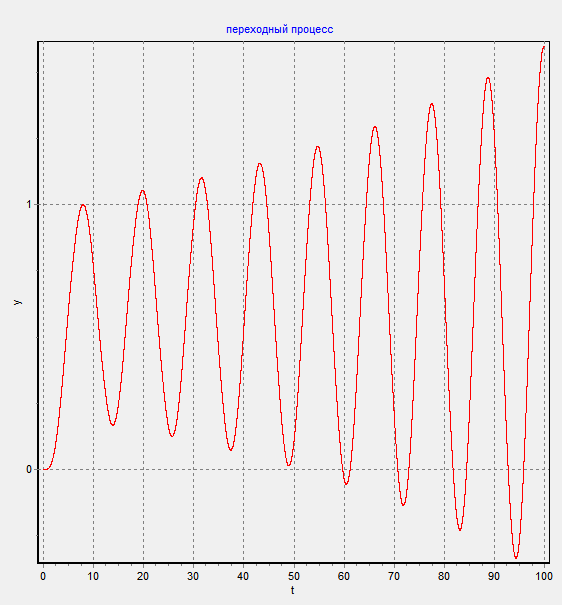
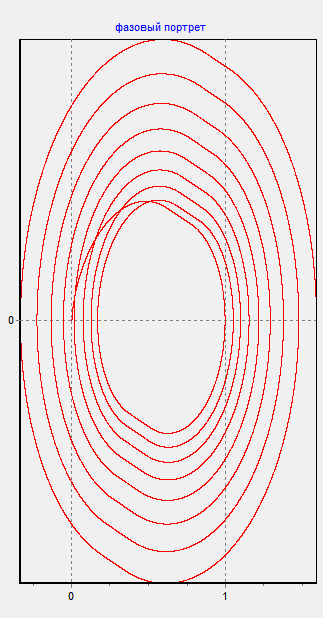
Вывод: Предельный цикл устойчив в малом и неустойчив в большом.