Переходные процессы в цепях с сосредоточенными параметрами

Выполнил: ст.гр

Проверил: проф.каф.ЭТЭ

САРАТОВ 2008

Вар.10. Сх.10. Емк.5.

Исходные данные

R₁=0 Ом, R₂=25 Ом, R₃=25 Ом, C=170 мкФ, E=100 В, L=0.125 Гн, Dt=0.01 сек.

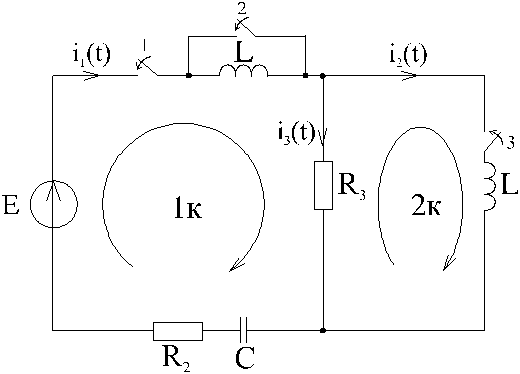
Рис.1

I. Для указанной схемы классическим методом найти i₁(t) после включения рубильников.

а). Первая коммутация (замыкание первого рубильника)

1). Определим независимые начальные условия для первой коммутации. До коммутации рубильники были выключены, поэтому i₁⁽¹⁾(-0)=i₁⁽¹⁾(+0)=0; u_C⁽¹⁾(-0)=u_C⁽¹⁾(+0)=0.

2). Запишем выражение для i₁⁽¹⁾(t) для первой коммутации в виде суммы свободной и принужденной составляющей i₁⁽¹⁾(t)=i_1св⁽¹⁾(t)+i_1пр⁽¹⁾.

Определим i_1пр⁽¹⁾ из послекоммутационной схемы в установившемся режиме. Постоянный ток не течет через конденсатор, следовательно i_1пр⁽¹⁾=0.

3). Составим характеристическое уравнение методом входного сопротивления

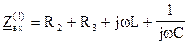
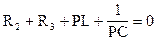
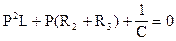
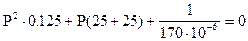
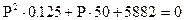
Найдем корни этого уравнения

D=b²-4ac=50²-4×0.125×5882=-441

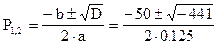=-200±j84=-d±jw_св

Корни характеристического уравнения получились комплексно-сопряженные, следовательно переходный процесс имеет колебательный характер и выражение для свободной составляющей i_1св⁽¹⁾(t) имеет вид:

i_1св⁽¹⁾(t)=Ae^-dtsin(w_свt+j).

Выражение для i₁⁽¹⁾(t) будет иметь следующий вид:

i₁⁽¹⁾(t)=i_1св⁽¹⁾(t)+i_1пр⁽¹⁾=Ae^-dtsin(w_свt+j),

так как i_1пр⁽¹⁾=0.

4). Определим А и j из начальных условий для первой коммутации:

i₁⁽¹⁾(0)=А×sinj=0; А¹0, следовательно sinj=0, следовательно j=0.

Возмем производную i₁⁽¹⁾(t)

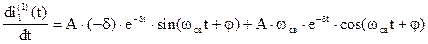
Определим величину производной 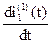в нулевой момент времени (t=0). Для этого запишем уравнения по второму закону Кирхгофа

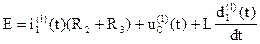(Ú)

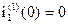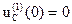; (см. начальные условия)

Тогда при t=0 уравнение (Ú) будет выглядеть следующим образом:

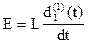
следовательно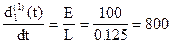

Тогда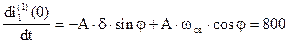

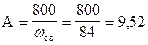
Таким образом получим выражение для тока 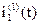при первой коммутации

i₁⁽¹⁾(t)=9,52×e^-200×t×sin(84×t+0)

б). Вторая коммутация (замыкание второго рубильника)

1). Определим независимые начальные условия для второй коммутации: u_C⁽²⁾(-0)=u_C⁽²⁾(+0)=u_C⁽¹⁾(Dt).

Для этого воспользуемся вторым законом Кирхгофа

=

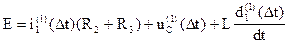
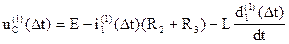
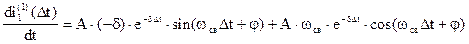=9,52×(-200)×e^-200×0,01×sin(84×0.01)+9,52×84×e^-200×0,01×cos(84×0.01)=-119,6

i₁⁽¹⁾(Dt)=9,52×e^-200×Dt×sin(84×Dt)=9,52×e^-200×0.01×sin(84×0.01)=0,96

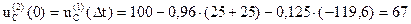
2). Запишем выражение для i₁⁽²⁾(t) для второй коммутации в виде суммы свободной и принужденной составляющей i₁⁽²⁾(t)=i_1св⁽²⁾(t)+i_1пр⁽²⁾.

Определим i_1пр⁽²⁾ из послекоммутационной схемы в установившемся режиме. После замыкания второго ключа постоянный ток не течет через конденсатор, следовательно i_1пр⁽²⁾=0.

3). Составим характеристическое уравнение для второй коммутации методом входного сопротивления

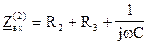
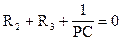
Найдем корень этого уравнения

;

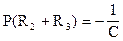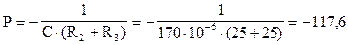
Корень характеристического уравнения получился один и действительный, следовательно переходный процесс имеет апериодический характер и выражение для свободной составляющей i_1св⁽²⁾(t) имеет вид:

i_1св⁽²⁾(t)=Ве^Pt=Be^-117,6×t

Выражение для i₁⁽¹⁾(t) будет иметь следующий вид:

i₁⁽²⁾(t)=Ве^Pt=Be^-117,6×t, так как i_1пр⁽¹⁾=0.

4). Определим B из начальных условий для второй коммутации. Для этого найдем i₁⁽²⁾(0), зная, что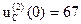

Запишем уравнение по второму закону Кирхгофа

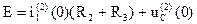
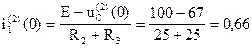
i₁⁽²⁾(0)=В=0,66

Таким образом получим выражение для тока 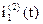при второй коммутации

i₁⁽²⁾(t)=0,66×e^-117,6×t

в). Третья коммутация (замыкание третьего рубильника)

1). Определим независимые начальные условия для третьей коммутации.

;

.

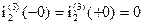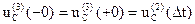u_C⁽²⁾(Dt) найдем из второго закона Кирхгофа для контура второй коммутации.

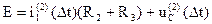, следовательно

,

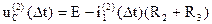где i₁⁽²⁾(Dt)=0,66×e^-117,6×Dt=0,66×e^-117×0,01=0,2

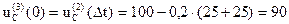
2). Запишем выражение для i₁⁽³⁾(t) для третьей коммутации в виде суммы свободной и принужденной составляющей i₁⁽³⁾(t)=i_1св⁽³⁾(t)+i_1пр⁽³⁾.

Определим i_1пр⁽³⁾ из послекоммутационной схемы в установившемся режиме. Постоянный ток не течет через конденсатор, следовательно i_1пр⁽³⁾=0.

3). Составим характеристическое уравнение методом входного сопротивления

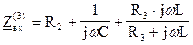
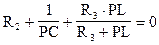
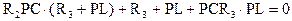
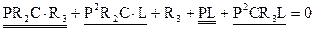
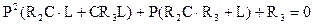
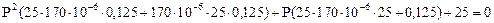
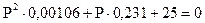
Найдем корни этого уравнения

D=b²-4ac=0,231²-4×0,00106×25=-0,0526

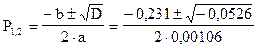=-109±j108=-d±jw_св

Корни характеристического уравнения получились комплексно-сопряженные, следовательно переходный процесс при третьей коммутации имеет колебательный характер и выражение для свободной составляющей i_1св⁽³⁾(t) имеет вид:

i_1св⁽³⁾(t)=De^-dtsin(w_свt+j).

Выражение для i₁⁽³⁾(t) будет иметь следующий вид:

i₁⁽³⁾(t)=i_1св⁽³⁾(t)+i_1пр⁽³⁾=De^-dtsin(w_свt+j),

так как i_1пр⁽³⁾=0.

4). Определим D и j из начальных условий для третьей коммутации. Для этого найдем i₁⁽³⁾(0) и 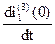зная, что 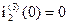и

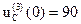
Запишем уравнения по законам Кирхгофа для узла а и первого контура

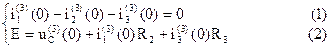
Из первого уравнения следует, что при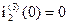

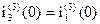(3)

Подставив (3) в (2) получим

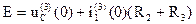
Отсюда определим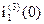

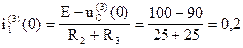
Дифференцируем уравнения (1) и (2) зная, что производная от напряжения на емкости равна току протекающему через эту емкость деленному на величину самой емкости, то есть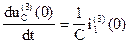

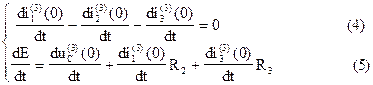
Выразим из уравнения (4)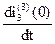

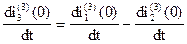(6)

Подставим (6) в (5)

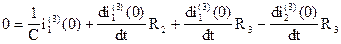(7)

Чтобы из уравнения (7) найти 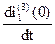необходимо знать 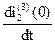, для определения которой запишем уравнение по второму закону Кирхгофа для второго контура

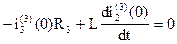, получим

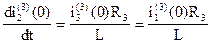(8)

Подставим (8) в (7)

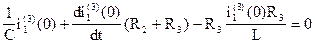, следовательно

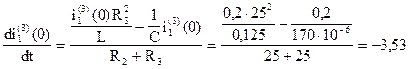
Возьмем производную от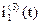

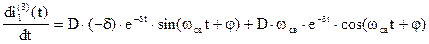
Используем начальные значения 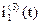и 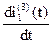для определения D и j.

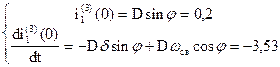
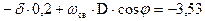
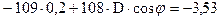
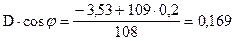
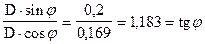, следовательно

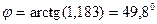
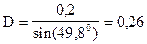
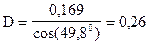
Таким образом получим выражение для тока 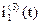при третьей коммутации

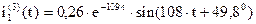
II. Найти 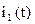операторным методом.

а). Первая коммутация.

1). Берем независимые начальные условия из классического метода

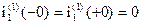
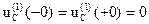
2). Составим операторную схему для первой коммутации (Рис.2). Внутренние ЭДС конденсатора и катушки индуктивности равны нулю, так 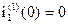и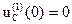

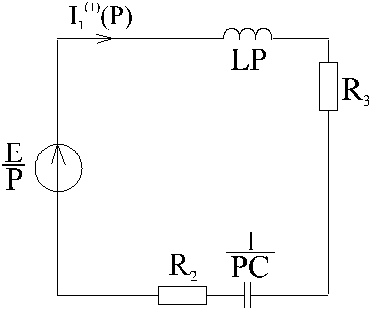
Рис.2

3). Ток 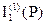определим по закону Ома

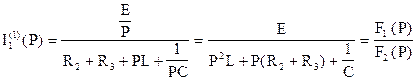
Полином знаменателя F₂(P) совпадает с характеристическим уравнением для первой коммутации и имеет те же корни P_1,2=-200±j84

4). По теореме разложения найдем оригинал тока

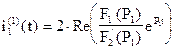, где

F₁(P)=E

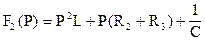
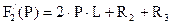
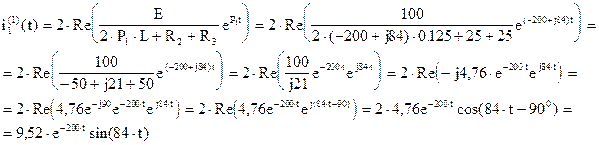Таким образом получим:

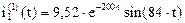
Выражение для тока 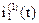при первой коммутации, полученное операторным методом, совпадает с решением, полученным классическим методом.

б). Вторая коммутация.

1). Берем независимые начальные условия из классического метода

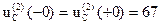
2). Составим операторную схему для второй коммутации (Рис.3).

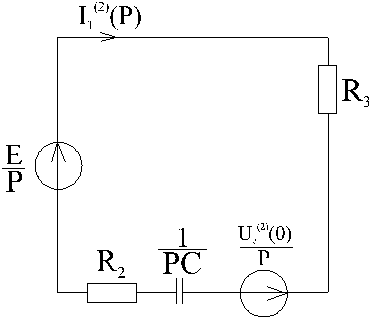
Рис.3

3). Ток 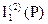определим по закону Ома

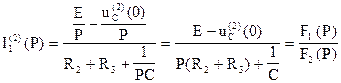
Полином знаменателя F₂(P) совпадает с характеристическим уравнением для второй коммутации и имеет тот же корень P=-117,6

4). По теореме разложения найдем оригинал тока

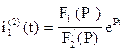, где

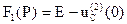
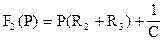
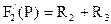
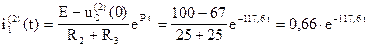
Таким образом получим:

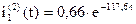
Выражение для тока 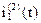при второй коммутации, полученное операторным методом, совпадает с решением, полученным классическим методом.

в). Третья коммутация.

1). Берем независимые начальные условия из классического метода

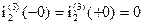
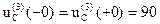
2). Составим операторную схему для третьей коммутации (Рис.4). Внутренняя ЭДС катушки индуктивности L₂ равна нулю, так .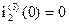

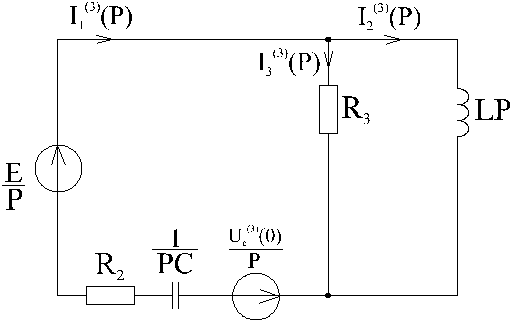
Рис.4

3). Ток 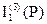определим по обобщенному закону Ома для полной цепи

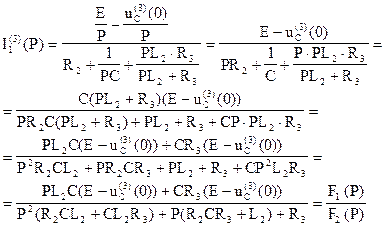
Полином знаменателя F₂(P) совпадает с характеристическим уравнением для третьей коммутации и имеет те же корни P_1,2=-109±j108

4). По теореме разложения найдем оригинал тока

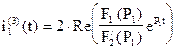, где

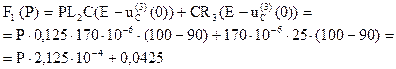
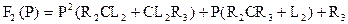
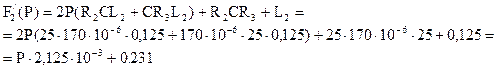
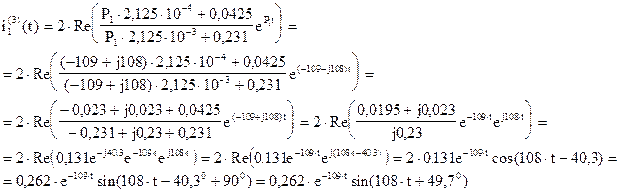Таким образом получим:

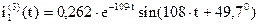
Выражение для тока 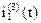при третьей коммутации, полученное операторным методом, совпадает с решением, полученным классическим методом.

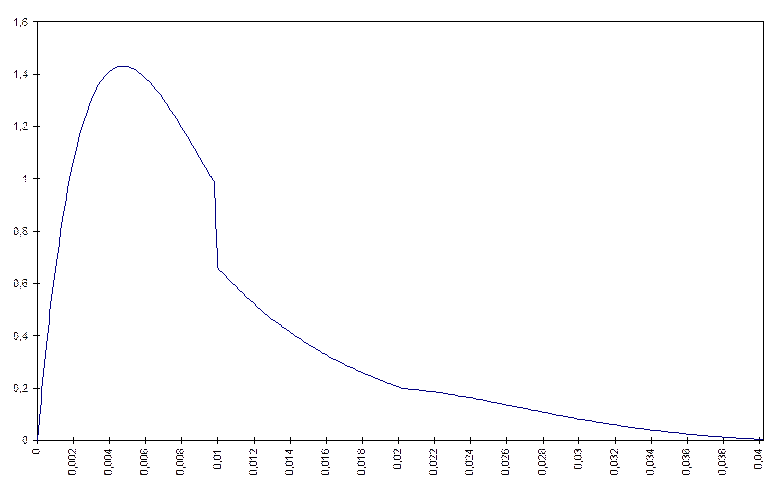
III. Построение графика.