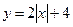Локальная и интегральные теоремы Лапласа.
0) Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) 75 раз; б) от 75 до 84 раз; в) менее 75 раз; г) не менее 70 раз.
1) Монету бросают 6 раз. найти вероятность того, что: а) герб выпадает три раза; б) герб выпадает один раз; в) герб выпадет не менее двух раз.
2) Стрелок четыре раза стреляет по мишени. Считая, что вероятность попадания при одном выстреле не зависит от результатов предшествующих выстрелов равна 0,8, найти вероятность того, что стрелок попал в мишень: а) два раза; б) не более трёх раз; в) хотя бы один раз; г) один раз.
3) в среднем 10% автомобилей, производимых заводом, имеют брак. Для контроля из партии автомобилей взяли 5 машин. Найти вероятность того, что среди них будет: а) 3 машины без брака; б) не более 3 машин без брака.
4) Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. В отдел магазина поступило 20 телевизоров. Что вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
5) Устройство состоит из 7 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,1. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента из семи.
6) Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течении одного часа он позвонит на станции, равна 0,02. Найти вероятность того, что в течении часа позвонят: а) 5 абонентов; б) не менее трех абонентов.
7) Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка разобьется, равна 0,03. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) более двух.
8) Среди семян пшеницы 0,6 % семян сорняков. Какова вероятность при случайном отборе 1000 семян обнаружить: а) ровно шесть семян сорняков; б) более трёх семян сорняков?
9) Игральную кость подбрасывают 180 раз. Найти вероятность того, что единица выпадет: а) 33 раза; б) от 20 до 29 раз; в) менее 35 раз; г) не менее 25 раз.
Тема 6. Дискретная случайная величина (ДСВ). Функция и характеристики распределения ДСВ
Задан закон распределения ДСВ X (см. ниже варианты заданий).
Найти:
а) неизвестную вероятность р;
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение s случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = f(x).
Варианты заданий по теме 6:
0)
| xi | -2 | -1 | |||||
| pi | 0,01 | p | 0,23 | 0,28 | 0,19 | 0,11 | 0,06 |

1)
| xi | -2 | -1 | |||||
| pi | 0,2 | 0,31 | 0,24 | p | 0,07 | 0,04 | 0,01 |
y = 2x + 3
2)
| xi | -2 | -1 | |||||
| pi | 0,04 | 0,08 | 0,3 | 0,3 | 0,1 | 0,08 | p |
y = x2– 1
3)
| xi | -2 | -1 | |||||
| pi | 0,42 | 0,23 | р | 0,10 | 0,06 | 0,03 | 0,01 |
y = –2x + 1
4)
| xi | -2 | -1 | |||||
| pi | р | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
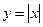
5)
| xi | -2 | -1 | |||||
| pi | 0,05 | 0,12 | 0,18 | 0,30 | р | 0,12 | 0,05 |
y = 5x – 2
6)
| xi | -2 | -1 | |||||
| pi | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | р | 0,03 |
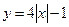
7)
| xi | -2 | -1 | |||||
| pi | 0,06 | р | 0,12 | 0,2 | 0,3 | 0,1 | 0,03 |
y = x2+ 2
8)
| xi | -2 | -1 | |||||
| pi | 0,02 | 0,38 | 0,30 | р | 0,08 | 0,04 | 0,02 |
y = x2+ 3
9)
| xi | -2 | -1 | |||||
| pi | 0,08 | 0,1 | 0,14 | 0,1 | 0,1 | 0,1 | р |