Метод измерения и описание аппаратуры. Цель работы. Ознакомление с методом измерения момен­тов инерции тел, обладающих осевой симметрией

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА МЕТОДОМ КОЛЕБАНИИ

Цель работы. Ознакомление с методом измерения момен­тов инерции тел, обладающих осевой симметрией.

Приборы и принадлежности: маховое колесо, добавочный груз в виде диска, штангенциркуль, секундомер.

Введение

Момент инерции тела I относительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:

I = mr²,

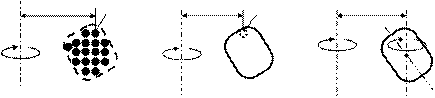
а для тела, которое можно представить в виде системы большого количества материальных точек (рис. 6.1.а), момент инерции относительно некоторой оси вращения равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:

I = .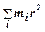

r_im_irdm О a

О¢

M

О I I₀

а) б) в) О¢

Рис. 6.1

Для вычисления момента инерции сплошного тела его мысленно разбивают на бесконечное малые области с массами dm,каждая из которых находится на своём расстоянии r от оси вращения (рис. 6.1.б); I находят интегрированием по всем этим областям:

I = .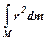

Понятно, что момент инерции зависит не только от общей массы тела, но и от формы тела, а также – от распределения массы по его объёму (так, например, какие-то части тела могут быть изготовлены из более тяжёлого материала, а какие-то – из более лёгкого).

Ось вращения может проходить через центр масс тела, а может и находиться вне его (рис. 6.1.в). Во втором случае для вычисления момента инерции пользуются вспомогательной формулой, которая выводится при доказательстве теоремы Штейнера (см. книги [1, 2]).

Момент инерции тела I относительно произвольной оси равен сумме момента инерции I₀ относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния а между осями:

I = I₀ + ma². (1)

При конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т.д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

В предлагаемой лабораторной работе изучается один из самых простых, но достаточно надёжных, методов измерения моментов инерции тел, обладающих осевой симметрией.

Метод измерения и описание аппаратуры

В работе определяется момент инерции махового колеса К, ось симметрии которого параллельна поверхности земли. Колесо находится в состоянии безразличного равновесия, но после крепления к нему добавочного груза Г (рис. 6.2), колесо может колебаться относительно горизонтальной оси.

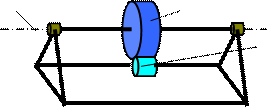Ось Маховое колесо К

Добавочный

груз Г

Рис. 6.2

Если пренебречь силами трения в подшипниках системы, то при малой амплитуде j₀ колебаний (j₀ < 5 ¸ 8°, при этом sinj₀ » tgj₀ » j₀) они окажутся гармоническими, то есть угол j отклонения системы от положения равновесия будет со временем t меняться по следующему закону:

j = j₀cos 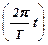. (2)

Здесь T- период колебаний системы, величина которого, как будет показано ниже, зависит от её момента инерции.

Маховое колесо начинает совершать колебания за счет сообщенной ему извне энергии. Добавочный груз Г, поднятый на высоту h относительно положения равновесия, обладает потенциальной энергией mgh(см. рис. 6.3).

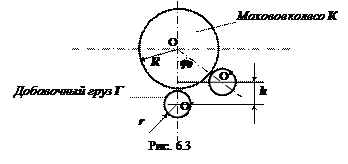При прохождении системой (Ки Г) положения равновесия потенциальная энергия груза Г преобразуется в кинетическую энергию вращательного движения махового колеса К и добавочного груза Г.Таким образом,

mgh = 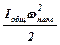, (3)

где I_общ - сумма моментов инерции махового колеса Iи добавочного груза I_Г относительно горизонтальной оси О, проходящий через центр махового колеса вдоль стержня:

I_общ = I+ I_Г; (4)

т - масса добавочного груза;

g - ускорение силы тяжести;

h - высота, на которую поднимается груз;

w_макс - угловая скорость махового колеса с грузом при прохождении системой положения равновесия.

Как следует из формул (3) и (4), для нахождения момента инерции махового колеса I нужно знать w_макс, т, h и I_Г.Угловая скорость w_макс определяется из уравнения (2) после установления характера зависимости w от времени t:

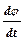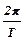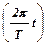w = = - j₀ sin . (5)

Из уравнения следует, что максимальное значение угловой скорости (по модулю) в момент прохождения системой положения равновесия равно:

w_макс = j₀ 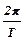. (6)

Высоту h поднятия центра инерции добавочного груза (см. рис. 6.3) можно выразить так:

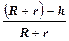= cosj₀,

где R и r - радиусы махового колеса и добавочного груза соответственно.

Следовательно,

h =(R + r)(1 - cosj₀). (7)

Подставляя в уравнение (3) найденные выражения для hи w_макс, получаем:

mg(R + r)(1 - cosj₀)= 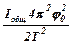. (8)

Величина j₀ неудобна для непосредственного измерения, поэтому исключим ее из уравнения (8). При малых углах, выраженных в радианной мере,

cosj₀ = 1 - 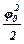. (9)

Подставив это значение косинуса в левую часть уравнения (8), получим формулу для расчета I_общ относительно оси О:

I_общ = 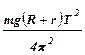. (10)

Момент инерции добавочного груза I_Г находим по теореме Штейнера. В лабораторной установке добавочный груз выполнен в виде диска из однородного материала и укреплен так, что его геометрическая ось параллельна оси симметрии махового колеса. Момент инерции добавочного груза Г относительно оси О (см. рис. 6.3) равен

I_Г = 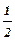mr² +m(R+r)². (11)

Первый член правой части равенства - момент инерции груза относительно оси О', проходящей через его центр масс параллельно оси О. Второе слагаемое – это произведение массы диска на квадрат расстояния между осями О и О'.

Из выражений (10) и (11) получаем, что момент инерции махового колеса

I = I_общ - I_Г = 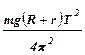- 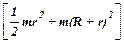. (12)

Таким образом, определение момента инерции махового колеса в данной работе удалось свести к измерению массы добавочного груза т, радиусов махового колеса R и добавочного груза r, а также – периода колебаний махового колеса Т.

Для того, чтобы подтвердить утверждение о высокой точности данного метода измерения момента инерции, предлагается сравнить полученное значение I с теоретическим (I_Т), которое для махового колеса – однородного диска можно вычислить по формуле:

I_Т= 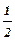m₀ R², (13)

где m₀ - масса махового колеса.

Учитывая, что маховое колесо и добавочный груз - диски одинаковой толщины, изготовленные из одного и того же материала (заметим, что для самого метода измерения момента инерции эти факторы несущественны), можно получить равенствоm₀ /m =R²/r².

Таким образом, массы дисков относятся, как их объемы или (при одинаковой толщине) – как квадраты их радиусов. Выразив из последнего уравнения массу m₀ и подставив её в формулу (13), получим

I_Т= 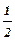mR⁴/r². (14)

В настоящей работе непосредственно измеряются диаметры махового колеса D и добавочного груза d, а также - время tдесяти полных колебаний. Масса груза m и ускорение свободного падения считаются заданными с известной степенью точности. Используя эти обозначения, окончательно запишем:

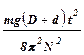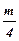
I = - 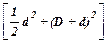, (15)

I_Т= 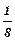mD⁴ / d². (16)

Порядок выполнения работы

Часть 1. Проведение измерений

1. Ознакомьтесь с измерительными приборами, используемыми в данной работе: штангенциркулем и секундомером. Определите значения приборной погрешности штангенциркуля (Dx) и секундомера (Dt); результаты запишите в таблицу 1.

2. Ознакомьтесь с установкой, на которой будете выполнять лабораторную работу. Значение массы добавочного груза m запишите в таблицу 1.

Таблица 1

Приборные погрешности	Масса добавочного груза m, кг
штангенциркуля Dx, м	секундомера Dt, с

Измерьте штангенциркулем диаметры махового колеса и добавочного груза с точностью, которую обеспечивает штангенциркуль. Результаты измерений занесите в таблицу 2.

Таблица 2

Номер измерения						Средние значения
Диаметр махового колеса D, м						Dср =
Диаметр добавочного груза d, м						dср =
Время десяти полных колебаний t, с						tср =
Период колебаний T, с						Tср =
Момент инерции махового колеса I, кг×м2						Iср = IТ =

4. Отклонив колесо с добавочным грузом на малый угол, удовлетворяющий соотношению (9), отсчитайте время tдесяти полных колебаний. Результаты измерений занесите в таблицу 2.

5. Повторите измерения по пп. 3 - 4 пять раз. Результаты измерений занесите в таблицу 2.

Часть 2. Обработка результатов измерений

Внимание! При проведении вычислений по пунктам 6 - 8 сохраняйте несколько значащих цифр после запятой. Округление итогового выражения для момента инерции махового колеса проводится только после вычисления ошибки измерений (см. пункт 9).

6. Вычислите значения периода колебаний махового колеса для всех пяти случаев.

7. Вычислите средние значения диаметров и махового колеса D_cp и d_срдобавочного груза, периода колебаний Т_ср, а затем, используя эти данные и формулу (15), рассчитайте, чему равно среднее значение момента инерции махового колеса I_ср. В вычислениях принять g= 9,81 м/с².

8. Используя полученные значения D_cp и d_ср, а такжезначение массы добавочного груза m, по формуле (16)рассчитайте теоретическое значение момента инерции махового колеса I_Т.

Результаты расчетов по пп. 6 - 8 занесите в таблицу 2.

9. Поскольку в эксперименте непосредственно измеряются лишь D, d и t, а величина момента инерции определяется косвенным образом из расчетов по формуле (15), для вычисления ошибки измерения I необходимо пользоваться формулами для расчета ошибок косвенных измерений. Окончательный результат должен быть записан в виде

I =I_cp ± DI, (17)

где DI - абсолютная ошибка измерения момента инерции махового колеса.

В данной работе основную роль в возникновении ошибки определения момента инерции играет случайная ошибка измерения периода колебаний; случайными же погрешностями измерения диаметров махового колеса и добавочного груза, а также - приборными ошибками штангенциркуля и секундомера можно пренебречь. В этом случае ошибка измерения момента инерции махового колеса вычисляется, как среднеквадратичная ошибка:

(DI)² = 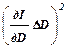+ + 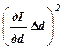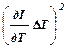» 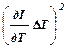. (18)

(Подробнее о методах расчета ошибок измерения физических величин см. методические указания [3] из списка рекомендуемой литературы).

Используя формулу (15), получим, что

DI » 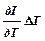= 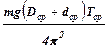DT . (19)

Таким образом, вычисление DI в данной работе сводится к определению случайной ошибки измерения периода колебаний DT:

DT = a 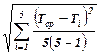, (20)

где a -коэффициент Стьюдента, значения которого можно найти в таблице, имеющейся в лаборатории (таблица приведена также в методических указаниях [3]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите равной 0,95.

10. Результат вычислений DI округлите до первой значащей цифры, после чего округлите полученные ранее (см. таблицу 2) значения I_ср и I_Т до того же разряда, что и DI.

Запишите окончательный численный результат в виде

I =I_cp ± DI, (21)

I_Т = ……

Обратите внимание на правильность записи единиц измерения, в которых выражены полученные значения момента инерции махового колеса.

Контрольные вопросы

1. Какое свойство тела выражает момент инерции и как он вычисляется для материальной точки и системы материальных точек? В каких единицах он измеряется в СИ?

2. Сформулируйте теорему Штейнера. Как она используется в данной работе?

3. Объясните, из каких соображений в данной работе выбирается число значащих цифр после запятой при округлении результатов вычислений.

5. В чём заключается физический принцип определения момента инерции методом колебаний?

4. Выведите формулы (12) и (14); укажите возможные причины некоторого несовпадения величин моментов инерции, определенных по этим формулам.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Савельев И.В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 1989.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов и др.; Под общ. ред. Ф.П.Денисова. - М.: МИИТ, 1995. – 38 с.