Каноническое распределение
Объект – равновесный идеальный газ из N частиц, находящихся в объеме V в термостате с температурой Т. Выполняется
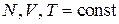 .
.
Газ обменивается энергией с термостатом через стенки сосуда. Энергия флуктуирует, микросостояния имеют разброс по энергии и по фазовому пространству. Получим вероятность обнаружения микросостояний в элементе объема фазового пространства и вероятность определенной энергии у микросостояния.
Распределение микросостояний по фазовому пространству.
Подсистемы идеального газа независимы друг от друга, потенциальная энергия их взаимодействия равна нулю. Гамильтонианы системы и подсистем 1 и 2 связаны соотношением
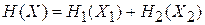 .
.
Распределения микросостояний по фазовому пространству выражаются через гамильтонианы согласно теореме Лиувилля
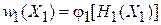 ,
,
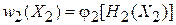 ,
,
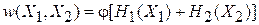 .
.
Для нахождения функций 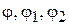 используем теорему умножения вероятностей независимых событий
используем теорему умножения вероятностей независимых событий
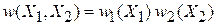 ,
,
получаем
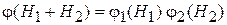 .
.
Логарифмируем
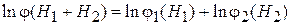 ,
,
берем дифференциал
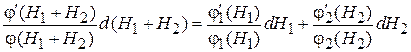 ,
,
где 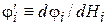 . Поскольку
. Поскольку 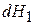 и
и 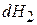 – независимые величины, то
– независимые величины, то
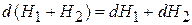 .
.
Равенство между функциями разных аргументов выполняется, если каждая из них равна одной и той же постоянной
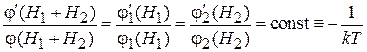 .
.
Далее показано, что k – постоянная Больцмана, T – температура. Следовательно, 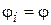 – универсальная функция гамильтониана, удовлетворяющая уравнению:
– универсальная функция гамильтониана, удовлетворяющая уравнению:
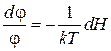 .
.
Интегрируем
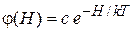 .
.
Нормировочную постоянную полагаем 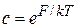 . Далее показано, что
. Далее показано, что 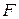 – свободная энергия системы. Получаем вероятность обнаружения микросостояния системы в единице объема фазового пространства около точки X, или плотность вероятностиканонического распределения
– свободная энергия системы. Получаем вероятность обнаружения микросостояния системы в единице объема фазового пространства около точки X, или плотность вероятностиканонического распределения
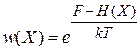 . (2.75)
. (2.75)
Вероятности обнаружения микросостояния в объеме dX фазового пространства около точки X
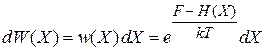 . (2.76)
. (2.76)
Статистический интеграл системы. Полагаем нормировочную постоянную 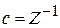 , тогда
, тогда
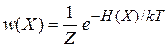 ,
,
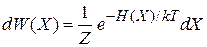 . (2.77)
. (2.77)
Нормировка вероятности
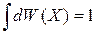
дает статистический интеграл системы
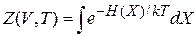 . (2.78)
. (2.78)
Сравниваем (2.75) и (2.77), находим
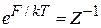 .
.
Логарифмируем и получаем соотношение между свободной энергией и статистическим интегралом
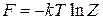 . (2.79)
. (2.79)
Статистический интеграл является макрохарактеристикой состояния системы, через Z выражаются термодинамические величины.
Статистический интеграл частицы. В идеальном газе частицы независимы друг от друга. Для N тождественных частиц
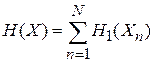 ,
, 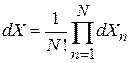 ,
,
где 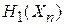 и
и 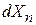 – гамильтониан и число микросостояний частицы n. С учетом свойства экспоненты
– гамильтониан и число микросостояний частицы n. С учетом свойства экспоненты 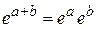 интеграл (2.78)
интеграл (2.78)
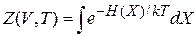
распадается на произведение N одинаковых интегралов. Получаем соотношение между статистическими интегралами системы и частицы
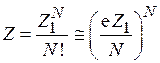 , (2.80)
, (2.80)
где при 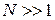 использована формула Стирлинга
использована формула Стирлинга
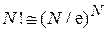 .
.
В результате выделена одна частица, остальные рассматриваются как термостат. Статистический интеграл частицы
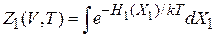 , (2.81)
, (2.81)
где
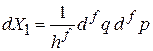 .
.
Для независимых видов движения частицы – поступательного, вращательного, колебательного и внутреннего, гамильтониан
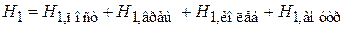 ,
,
тогда из (2.81) находим
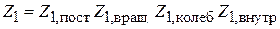 . (2.82)
. (2.82)
Для N частиц
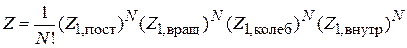 .
.
Для поступательного движения получено (П.3.2)
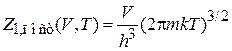 . (2.83)
. (2.83)
Для вращения и колебания двухатомной молекулы с моментом инерции J и частотой собственного колебания w найдено (П.3.8) – (П.3.10)
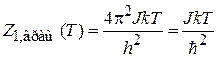 , (2.84)
, (2.84)
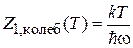 . (2.85)
. (2.85)
Распределение микросостояний частицы по фазовому пространству. Выделяем одну частицу газа, рассматривая остальные как термостат. Из (2.77)
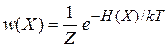 ,
,
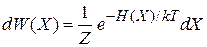
получаем плотность вероятности и вероятность обнаружения микросостояния частицы в фазовом пространстве
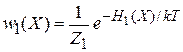 ,
,
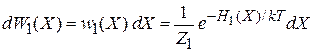 . (2.86)
. (2.86)
Физический смыслT. Докажем, что параметр Т в каноническом распределении является температурой. Используем общее начало термодинамики– если температура систем одинаковая, то приведение систем в тепловой контакт не изменяет их макросостояний. До контакта систем 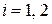 их функции распределения (2.75)
их функции распределения (2.75)
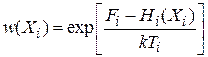 .
.
В момент контакта в силу независимости систем общее распределение по теореме умножения вероятностей равно
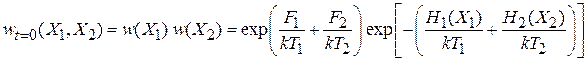 .
.
С течением времени, гораздо меньшем времени теплообмена с окружением, системы перемешиваются за счет броуновского движения. Гамильтонианы изменяются, их сумма сохраняется. Если температуры систем были одинаковыми, то распределение не должно меняться согласно общему началу термодинамики. Для рассматриваемой функции это выполняется при 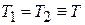 . Следовательно, Т – температура.
. Следовательно, Т – температура.
