Взаимное расположение прямых и плоскостей в пространстве
17.1. Найти точку пересечения прямой и плоскости
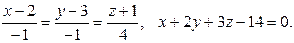
17.2. Найти проекцию точки М(1,0,-1) на прямую 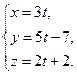
17.3. Найти проекцию точки М(-1,-2,3) на прямую 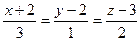 .
.
17.4. Найти проекцию точки М(1,1,1) на прямую, проходящую через точки А(2,5,-3) и В(3,-2,2).
17.5. Найти проекцию точки М(5,2,-1) на плоскость 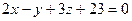 .
.
17.6. Найти точку А, симметричную точке В(2,-5,7) относительно прямой, проходящей через точки 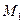 (5, 4, 6) и
(5, 4, 6) и 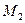 (-2, -17, -8).
(-2, -17, -8).
17.7. Найти точку А, симметричную точке B(1,2,3) относительно прямой:
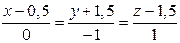
17.8. Составить уравнение плоскости, проходящей через точку А(1, 1, 1) параллельно прямым 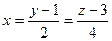 и
и 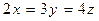 .
.
17.9. Составить уравнение плоскости, проходящей через прямую 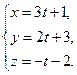 параллельно прямой
параллельно прямой 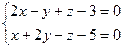 .
.
17.10. Составить уравнение плоскости, проходящей через прямую 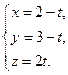 и точку Р(0, 0, 0).
и точку Р(0, 0, 0).
17.11. Доказать, что прямые 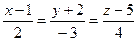 и
и 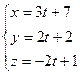 лежат в одной плоскости и составить ее уравнение.
лежат в одной плоскости и составить ее уравнение.
17.12. Найти уравнения прямой, проходящей через точку М(3,-2,4) параллельно плоскости 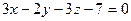 и пересекающей прямую
и пересекающей прямую 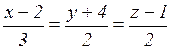 .
.
17.13. Написать канонические уравнения прямой, образованной пересечением плоскости 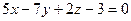 с плоскостью Oyz.
с плоскостью Oyz.
17.14. Найти расстояние между прямыми 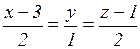 и
и 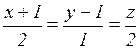 . Составить уравнение плоскости, проходящей через эти прямые.
. Составить уравнение плоскости, проходящей через эти прямые.
Занятие № 18.
Поверхности в пространстве.
18.1. Определить тип поверхности второго порядка при различных значениях параметра k:
а) 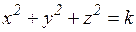 ; б)
; б) 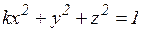 ; в)
; в) 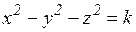 ;
;
г) 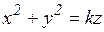 ; д)
; д) 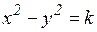 .
.
18.2. Составить уравнение сферы с центром в точке А(1,1,1) и радиусом 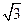 .
.
18.3. Найти координаты центра А и радиус сферы R:
а) 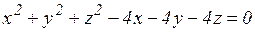 ;
;
б) 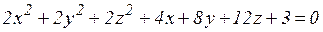 .
.
18.4. Найти координаты центра поверхности и вершин, ее полуоси и уравнения плоскостей симметрии, оси симметрии, изобразить поверхность в исходной системе координат:
а) 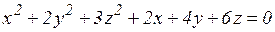 ;
;
б) 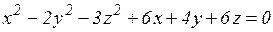 .
.
18.5. Определить тип поверхности:
а) 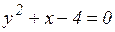 ;
;
б) 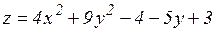 ;
;
в) 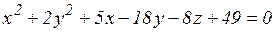 ;
;
г) 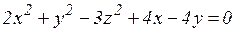 ;
;
д) 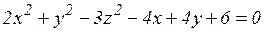 ;
;
е) 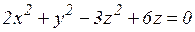 ;
;
ж) 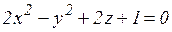 ;
;
з) 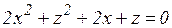 .
.
18.6. Определить тип поверхности:
а) 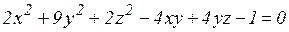 ;
;
б) 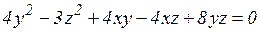 ;
;
в) 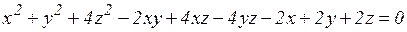 ;
;
г) 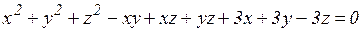 ;
;
д) 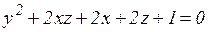 .
.
Введение в математический анализ.
Занятие № 19.
Числовые функции и их свойства.
19.1. Найти область определения функции:
а) 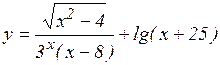 ; б)
; б) 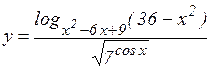 ;
;
в) 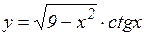 ; г)
; г) 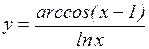 ; д)
; д) 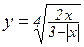 ;
;
е) 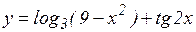 ; ж)
; ж) 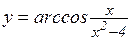 ;
;
Найти множество значений функции
а) 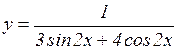 ; б)
; б) 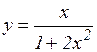 ; в)
; в) 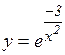 ; г)
; г) 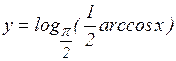 ;
;
д) 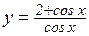 ; е)
; е) 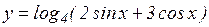 ;
;
19.3. Исследовать на четность или нечетность следующие функции:
а) 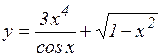 ; б)
; б) 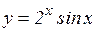 ; в)
; в) 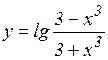 ; г)
; г) 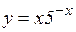 ;
;
д) 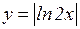 ; е)
; е) 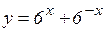 ; ж)
; ж) 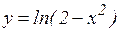 ; з)
; з) 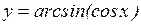 .
.
19.4. Найти основной (наименьший) период функции или доказать ее непериодичность:
а) 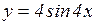 ; б)
; б) 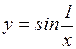 ; в)
; в) 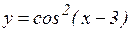 ; г)
; г) 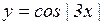 ;
;
д) 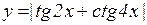 ; е)
; е) 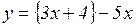 ;
;
ж) 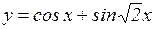 ; з)
; з) 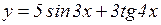 .
.
19.5. Дана функция 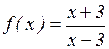 . Найти
. Найти 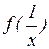 .
.
19.6. Исследовать функции на ограниченность:
а) 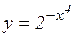 ; б)
; б) 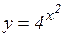 ; в)
; в) 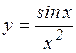 ; г)
; г) 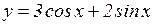 ; д)
; д) 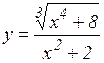 ;
;
е) 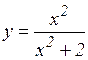 ; ж)
; ж) 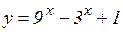 ; з)
; з) 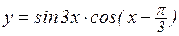 .
.
19.7. Какие из следующих функций являются монотонными на множестве всех действительных чисел?
а) 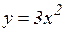 ; б)
; б) 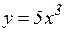 ; в)
; в) 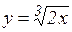 ; г)
; г) 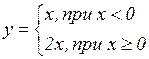 ;
;
д) 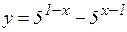 ; е)
; е) 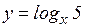 ; ж)
; ж) 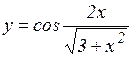 ; з)
; з) 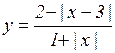 .
.
19.8. Какие из следующих функций являются обратимыми?
а) 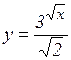 ; б)
; б) 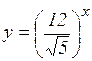 ; в)
; в) 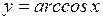 ; г)
; г) 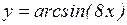 ;
;
д) 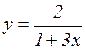 ; е)
; е) 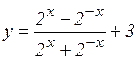 ; ж)
; ж) 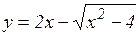 ; з)
; з) 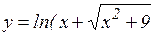 .
.
19.9. Построить график уравнения:
а) 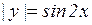 ; б)
; б) 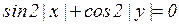 ; в)
; в) 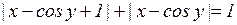 .
.
19.10. Доказать, что функция, обратная к возрастающей (убывающей), является возрастающей (убывающей).
Занятие № 20.
Элементарные преобразования графиков функций.
20.1. Используя элементарные преобразования, построить графики следующих функций:
а) 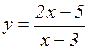 ; б)
; б) 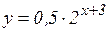 ; в)
; в) 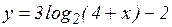 ;
;
г) 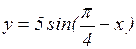 ; д)
; д) 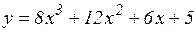 ; е)
; е) 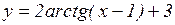 .
.
20.2. Построить графики следующих функций, заданных параметрически:
а) 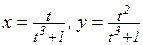 ; б)
; б) 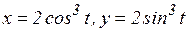 ;
;
в) 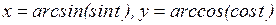 ; г)
; г) 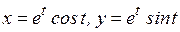 ;
;
д) 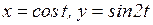 ; е)
; е) 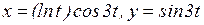 .
.
20.3. Построить графики следующих кривых, заданных в полярной системе координат уравнениями:
а) 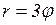 ; б)
; б) 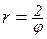 ; в)
; в) 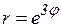 ; г)
; г) 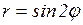 ; д)
; д) 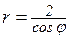 ; е)
; е) 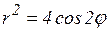 .
.
Занятие № 21.
Предел числовой последовательности.
