Математико-статистические таблицы

Приложение 1

Методические указания к использованию таблиц

1. В ТАБЛИЦЕ 1 протабулирована функция (интеграл вероятностей) Лапласа:

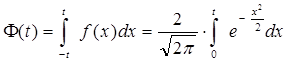
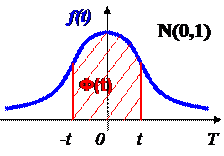
где f(t) - плотность нормированной (стандартной) нормально распределенной случайной величины T 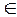N(0,1)

Ф(t) обладает следующими свойствами:

1. Ф(t) – нечётная функция: Ф(-t) = - Ф(t);

2. Ф(t) – монотонно возрастающая функция: при t®+¥ Ф(t) ®1; Ф(+ 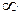) = 1.

Вероятность попадания случайной величины Т в интервал от t₁ до t₂ вычисляется по формуле:

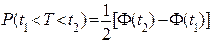
Пример 1.T 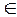N(0,1) P(-1,36<T<2,15)=?

На пересечении строки, соответствующей t=1,3 и столбца, соответствующего 6 сотым долям t, находим в середине таблицы значение функции Лапласа. Это Ф(t)= 0,8262. Таким образом, с учётом нечётности функции Лапласа, t₁=-1,36 соответствует Ф(t₁)=Ф(-1,36)=-Ф(1,36)=-0,8262.

Аналогично t₂=2,15 соответствует Ф(t₂)=Ф(2,15)=0,9684

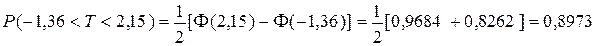
Пример 2. Ф(t)=0,98; t=?

В середине таблицы находятся значения функции Лапласа Ф(t). Находим ближайшее к 0,98 значение, это Ф(t)=0,9802. Значит, соответствующее значение t будет равно 2,33. t=2,33.

2.В ТАБЛИЦЕ 2 протабулирована вероятность выхода за пределы интервала от -t до +t случайной величины, имеющей распределение Стьюдента (t - распределение) с числом степеней свободы :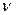

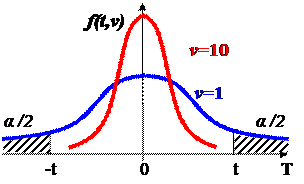
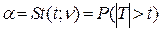
f(t;ν) - плотность распределения Стьюдента с числом степеней свободы ν.

Функция St(t) обладает следующими свойствами:

1. St(-t) = 2 - St(t);

2. St ( 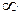) = 0; St (- 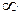) = 2; St (0) = 1.

Вероятность попадания случайной величины T в интервал от t₁ до t₂ вычисляется по формуле:

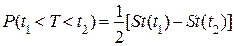
Пример 1. Для заданной вероятности α=0,05 и числа степеней свободы ν=12 найти соответствующее значение t.

На пересечении строки таблицы, соответствующей ν=12, и столбца, в котором α=0,05 , находим значение t=2,179.

Пример 2.Определить, какой вероятности α соответствует найденное значение t=1,19 при числе степеней свободы ν=8.

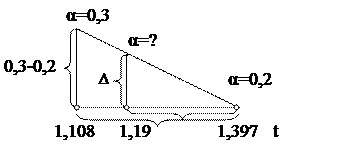В строке, соответствующей заданному числу степеней свободы ν=8, находим ближайшее значение к t=1,19 - это t=1,108, что соответствует вероятности α=0,3.

Более точно значение вероятности α можно найти методом линейной интерполяции.

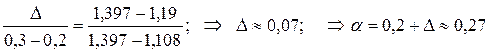
Пример 3. при 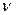= 10 определить P(-1,36<T<2,15)=?

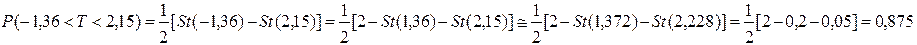Чтобы не прибегать к интерполяции, в строке, соответствующей 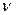=10, находим ближайшие к заданным значения.

3.В ТАБЛИЦЕ 3 протабулирована вероятность того, что наблюдаемое значение случайной величины χ², имеющей распределение Пирсона (хи-квадрат распределение) с числом степеней свободы n, превысит табличное значение χ²_T

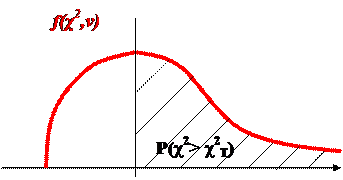На рисунке представлен график функции f(χ²,ν) - плотности c² - распределения с числом степеней свободы n.

Вероятность попадания случайной величины c² в интервал от c₁² до c₂² вычисляется по формуле

.

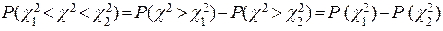Функция P(c²) обладает следующими свойствами:

0 χ2T χ2

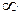P (0) = P(c²>0) = 1; P (+ ) = P(c²>+ 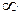) = 0.

Пример 1.При числе степеней свободы 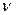=8 и вероятностям, равным P(c₁²)=0,975 и P(c₂²)=0,025, найти соответствующие значения c₁² и c₂².

На пересечении строки таблицы, соответствующей ν=8, и столбца, в котором P(c_T²)=0,975, находим значение c₁²=2,180. Аналогично на пересечении строки с ν=8, и столбца, в котором P(c_T²)=0,025, находим значение c₂²=17,535.

Пример 2.При числе степеней свободы 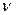=12 и значениям c₁²=3,156 и c₂²=20,48 найти соответствующие им

вероятности P(c₁²) и P(c₂²).

В строке, соответствующей заданному числу степеней свободы ν=12, находим ближайшее значение к c₁²=3,156 - это c₁²=3,074, что соответствует вероятности P(c₁²)=0,995. Аналогично в строке с ν=12, находим ближайшее значение к c₂²=20,48 - это c₂²=21,026, что соответствует вероятности P(c₂²)=0,05.

Более точно значение вероятностей P(c²) можно найти методом линейной интерполяции, приведённым в описании таблицы 2.

Пример 3.При числе степеней свободы 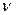=10 определить

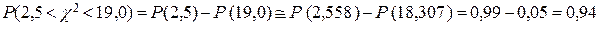
Чтобы не прибегать к интерполяции, в строке таблицы, соответствующей 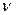=10, берём значения, ближайшие к заданным.

f(F)

4. В ТАБЛИЦЕ 4 для случайной величины F, имеющей закон распределения Фишера-Снедекора (F-распределение) с числами степеней свободы числителя ν₁ и знаменателя ν₂, протабулированы три значения, соответствующие трем вероятностям (уровням значимости): α=P(F>F_T)=0,05 (верхнее значение); α= 0,01 (среднее значение) и α=0,001(нижнее значение).

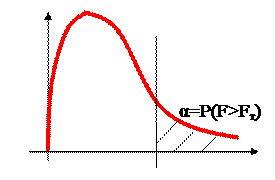
Статистика F строится таким образом, чтобы наблюдаемое значение было не меньше единицы (числитель должен быть больше знаменателя).

0 FT F

Пример.Найти значение F-распределения, соответствующее уровню значимости α = 0,01 и числам степеней свободы числителя ν₁=5 и знаменателя ν₂=7.

На пересечении столбца таблицы, соответствующего числу степеней свободы числителя ν₁=5, и строки, соответствующей числу степеней свободы знаменателя ν₂=7, находим три значения F-распределения и выбираем среднее из них, соответствующее α = 0,01. Таким образом, F_T=7,46.

5.В ТАБЛИЦЕ 5 Фишера - Иейтсаприведены критические значения коэффициента корреляции r_кр(α;ν) для проверки значимости генеральных парных и частных коэффициентов корреляции по выборочным.

В таблице приведены значения для четырёх уровней значимости: α=0,05; α=0,02; α=0,01 и α=0,001.

Число степеней свободы ν зависит от объёма выборки n и вида коэффициента корреляции. n = n - 2 в случае парной корреляции и n = n - l - 2, где l - число исключенных величин, в случае частной корреляции.

Пример.Найти критические значения коэффициента корреляции r_кр(α;ν) для проверки значимости

r_кр(α=0,02; ν=21) находится на пересечении строки таблицы, соответствующей ν=21 и столбца со значением α=0,02 в верхней части таблицы (для двусторонних границ). ν=21 отсутствует, поэтому методом линейной парных и частных коэффициентов корреляции в случае трёхмерной модели (X,Y,Z) на уровне значимости α=0,02, если число наблюдений, по которым рассчитаны выборочные коэффициенты корреляции, равно n=23.

При проверке значимости парных коэффициентов корреляции ρ_xy, ρ_yz, ρ_xz число степеней свободы n =n-2=21. интерполяции находим недостающее значение r_кр для ν=21 между r_кр=0,492 (для ν=20) и r_кр=0,445 (для ν=25). Повышение степени свободы на 1 соответствует понижению r_кр на (0,492-0,445)/5=0,0094; следовательно, r_кр(ν=21)=0,492-0,0094=0,4826. Таким образом, для парных коэффициентов корреляции r_кр=0,4826.

При проверке значимости частных коэффициентов корреляции ρ_xy/z, ρ_yz/x, ρ_xz/y число степеней свободы n=n-l-2=23-1-2=20 (l=1 в случае трёхмерной модели, фиксируется одна переменная). r_кр(α=0,02; ν=20) находится на пересечении строки таблицы, в которой ν=20 и столбца со значением α=0,02 в верхней части таблицы (для двусторонних границ). Таким образом, для частных коэффициентов корреляции r_кр=0,492.

6.В ТАБЛИЦЕ 6приведены значения прямого и обратного Z-преобразования Фишера, соответствующие гиперболическим арктангенсам и гиперболическим тангенсам заданных чисел.

;

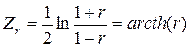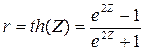
Используются в математической статистике при расчёте интервальных оценок генеральных коэффициентов корреляции. Для значимых выборочных парных и частных коэффициентов корреляции можно построить с заданной надёжностью γ доверительный интервал ρ_min ≤ ρ ≤ ρ_max с помощью Z-преобразования Фишера:

;

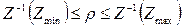
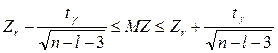Пример. Для выборки из 15 наблюдений двумерной нормальной совокупности (X,Y) получено, что выборочный коэффициент корреляции равен r=-0,85. С надёжностью γ=0,95 построить доверительный интервал для генерального коэффициента корреляции ρ_min ≤ ρ ≤ ρ_max.

1). По найденному выборочному коэффициенту корреляции r=0,85 с помощью таблицы 6 находим соответствующее значение Z_r на пересечении строки, в которой r=0,8 и столбца, соответствующего 5 сотым долям r. Таким образом, получаем Z_r=-1,2562. (Z(-r)=-Z(r) , т.к. Z(r) - функция нечётная)

2). Вычисляем 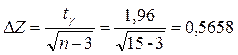(t_γ=1,96 , соответствующее заданной надёжности γ=0,95 , находим по таблице 1 функции Лапласа для Ф(t_γ)=γ=0,95).

Затем рассчитываем Z_min = Z_r – ΔZ=-1,2562-0,5658=-1,822; Z_max= Z_r + ΔZ=-1,2562+0,5658=-0,6904.

3). Соответствующие значения ρ_min и ρ_max находятся с помощью обратного преобразования Фишера следующим образом. В середине таблицы 6 находим ближайшие к рассчитанным Z_min и Z_max значения и определяем, каким коэффициентам корреляции они соответствуют.

Z_min=-1,822; в середине таблицы 6 находим ближайшее значение, это Z=1,8318. Это соответствует коэффициенту корреляции, равному 0,95 (смотрим, на пересечении каких строки и столбца находится найденное значение Z). Следовательно, нижняя граница генерального коэффициента корреляции ρ_min=-0,95.

Аналогично для Z_max=-0,6904 в середине таблицы 6 находим ближайшее значение, это Z=0,6932. Это соответствует коэффициенту корреляции, равному 0,60. Следовательно, верхняя граница генерального коэффициента корреляции ρ_max=-0,60. (Более точно значения ρ_min и ρ_max можно получить, рассчитав по формуле гиперболического тангенса, приведённой выше). Таким образом, Р(-0,95≤ ρ ≤ -0,60)= γ=0,95.

7. В ТАБЛИЦЕ 7 протабулирована функция плотности вероятностей (функция Гаусса) f(t) нормирован-ной (стандартной) нормально распределенной случайной величины T 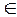N(0,1)

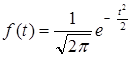
f(t) обладает следующими свойствами:

1. f(t) – чётная функция: f(-t) = f(t). Функция f(t) симметрична относительно оси ординат

2. f(t) – монотонно убывающая функция: при t®±¥ f(t) ®0; f(+ 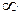) = 0.

Пример 1.T 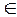N(0,1); t=1,53; f(t)=?

На пересечении строки, соответствующей t=1,5 и столбца, соответствующего 3 сотым долям t, находим в середине таблицы значение функции Гаусса f(t)=0,1238.

Пример 2.T 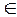N(0,1); f(t)=0,31; t=?

В середине таблицы находим значение функции Гаусса, ближайшее к заданному 0,31. Это f(t)=0,3101. Теперь смотрим, какому t это соответствует, т.е на пересечении каких строки и столбца находится найденное значение f(t). Таким образом, получаем t=0,71.

8.В ТАБЛИЦЕ 8 протабулированы значения функции Пуассона вероятности того, что в n повторных независимых испытаниях событие А наступит ровно m раз. Формула Пуассона используется при вероятности наступления события p, близкой к нулю, и параметруλ=np,находящемуся в пределах0,1 ≤ λ ≤ 10.

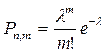
Пример.Событие А происходит в каждом из испытаний с вероятностью p=0,005. Найти вероятность, что при проведении 1000 испытаний событие А наступит 3 раза.

n=1000; m=3; p=0,005. P₁₀₀₀(X=3)=?

λ=np=1000·0,005=5. Искомую вероятность находим в таблице 8 на пересечении строки, соответствующей m=3 и столбца, в котором λ=5. Таким образом, P₁₀₀₀(X=3)= 0,1404.

9.В ТАБЛИЦЕ 9приведены значения G – распределения.Используется в математической статистике при проверке гипотезы об однородности ряда дисперсий k генеральных совокупностей с помощью критерия Кохрана. Значения G – распределения приводятся в таблице для двух уровней значимости. Первое значение соответствует уровню значимости a = 0,05, а второе - a = 0,01.

Кроме того, значение G зависит от числа степеней свободыν= n-1(где n – объём независимых выборок из каждой совокупности)и количества рассматриваемых совокупностейk, для которых проверяется равенство генеральных дисперсий.

Пример.Для проверки гипотезы о равенстве генеральных дисперсий 4 совокупностей осуществили независимые выборки по 10 наблюдений в каждой. Критерий Кохрана проверяется на уровне значимости a=0,05. Найти соответствующее значение G-распределения G_кр .

На пересечении строки таблицы 9, соответствующей k=4, и столбца, в котором число степеней свободы ν=n-1=10-1=9 находятся два значения G-распределения. Берём верхнее из них, соответствующее заданному уровню значимости a=0,05. Таким образом, G_кр=0,502.

Таблица 1

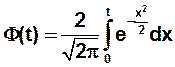Нормальный закон распределения

З н а ч е н и я ф у н к ц и и Л а п л а с а Ф(t) = P (|T| £ t_табл) Ф(-t) = - Ф(t)

Целые и десятые доли t	С о т ы е д о л и t
0,0	0,0000	0,0080	0,0160	0,0239	0,0319	0,0399	0,0478	0,0558	0,0638	0,0717
0,1	0,0797	0,0876	0,0955	0,1034	0,1113	0,1192	0,1271	0,1350	0,1428	0,1507
0,2	0,1585	0,1663	0,1741	0,1819	0,1897	0,1974	0,2051	0,2128	0,2205	0,2282
0,3	0,2358	0,2434	0,2510	0,2586	0,2661	0,2737	0,2812	0,2886	0,2960	0,3035
0,4	0,3108	0,3182	0,3255	0,3328	0,3401	0,3473	0,3545	0,3616	0,3688	0,3759
0,5	0,3829	0,3899	0,3969	0,4039	0,4108	0,4177	0,4245	0,4313	0,4381	0,4448
0,6	0,4515	0,4581	0,4647	0,4713	0,4778	0,4843	0,4907	0,4971	0,5035	0,5098
0,7	0,5161	0,5223	0,5285	0,5346	0,5407	0,5467	0,5527	0,5587	0,5646	0,5705
0,8	0,5763	0,5821	0,5878	0,5935	0,5991	0,6047	0,6102	0,6157	0,6211	0,6265
0,9	0,6319	0,6372	0,6424	0,6476	0,6528	0,6579	0,6629	0,6679	0,6729	0,6778
1,0	0,6827	0,6875	0,6923	0,6970	0,7017	0,7063	0,7109	0,7154	0,7199	0,7243
1,1	0,7287	0,7330	0,7373	0,7415	0,7457	0,7499	0,7540	0,7580	0,7620	0,7660
1,2	0,7699	0,7737	0,7775	0,7813	0,7850	0,7887	0,7923	0,7959	0,7994	0,8029
1,3	0,8064	0,8098	0,8132	0,8165	0,8198	0,8230	0,8262	0,8293	0,8324	0,8355
1,4	0,8385	0,8415	0,8444	0,8473	0,8501	0,8529	0,8557	0,8584	0,8611	0,8638
1,5	0,8664	0,8690	0,8715	0,8740	0,8764	0,8789	0,8812	0,8836	0,8859	0,8882
1,6	0,8904	0,8926	0,8948	0,8969	0,8990	0,9011	0,9031	0,9051	0,9070	0,9090
1,7	0,9109	0,9127	0,9146	0,9164	0,9181	0,9199	0,9216	0,9233	0,9249	0,9265
1,8	0,9281	0,9297	0,9312	0,9327	0,9342	0,9357	0,9371	0,9385	0,9399	0,9412
1,9	0,9426	0,9439	0,9451	0,9464	0,9476	0,9488	0,9500	0,9512	0,9523	0,9534

Окончание табл. 1

Целые и десятые доли t	С о т ы е д о л и t
2,0	0,9545	0,9556	0,9566	0,9576	0,9586	0,9596	0,9606	0,9616	0,9625	0,9634
2,1	0,9643	0,9651	0,9660	0,9668	0,9676	0,9684	0,9692	0,9700	0,9707	0,9715
2,2	0,9722	0,9729	0,9736	0,9743	0,9749	0,9756	0,9762	0,9768	0,9774	0,9780
2,3	0,9786	0,9791	0,9797	0,9802	0,9807	0,9812	0,9817	0,9822	0,9827	0,9832
2,4	0,9836	0,9841	0,9845	0,9849	0,9853	0,9857	0,9861	0,9865	0,9869	0,9872
2,5	0,9876	0,9879	0,9883	0,9886	0,9889	0,9892	0,9895	0,9898	0,9901	0,9904
2,6	0,9907	0,9910	0,9912	0,9915	0,9917	0,9920	0,9922	0,9924	0,9926	0,9928
2,7	0,9931	0,9933	0,9935	0,9937	0,9939	0,9940	0,9942	0,9944	0,9946	0,9947
2,8	0,9949	0,9951	0,9952	0,9953	0,9955	0,9956	0,9958	0,9959	0,9960	0,9961
2,9	0,9963	0,9964	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972
3,0	0,9973	0,9974	0,9975	0,9976	0,9976	0,9977	0,9978	0,9979	0,9979	0,9980
3,1	0,9981	0,9981	0,9982	0,9983	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986
3,2	0,9986	0,9987	0,9987	0,9988	0,9988	0,9988	0,9989	0,9989	0,9990	0,9990
3,3	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,4	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995	0,9995
3,5	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997	0,9997
3,6	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998	0,9998	0,9998
3,7	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,9	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
4,0	0,999937	0,999939	0,999942	0,999944	0,999947	0,999949	0,999951	0,999953	0,999955	0,999957
4,5	0,999993	0,999994	0,999994	0,999994	0,999994	0,999995	0,999995	0,999995	0,999995	0,999996
5,0	0,9999994	-	-	-	-	-	-	-	-	-

Таблица 2

Р а с п р е д е л е н и е С т ь ю д е н т а (t-распределение)

n	В е р о я т н о с т ь a = St (t) = P (|T| > tтабл)
0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0,05	0,02	0,01	0,001
	0,158	0,325	0,510	0,727	1,000	1,376	1,963	3,078	6,314	12,706	31,821	63,657	636,619
	0,142	0,289	0,445	0,617	0,816	1,061	1,386	1,886	2,920	4,303	6,965	9,925	31,598
	0,137	0,277	0,424	0,584	0,765	0,978	1,250	1,638	2,353	3,182	4,541	5,841	12,941
	0,134	0,271	0,414	0,569	0,741	0,941	1,190	1,533	2,132	2,776	3,747	4,604	8,610
	0,132	0,267	0,408	0,559	0,727	0,920	1,156	1,476	2,015	2,571	3,365	4,043	6,859
	0,131	0,265	0,404	0,553	0,718	0,906	1,134	1,440	1,943	2,447	3,143	3,707	5,959
	0,130	0,263	0,402	0,549	0,711	0,896	1,119	1,415	1,895	2,365	2,998	3,499	5,405
	0,130	0,262	0,399	0,546	0,706	0,889	1,108	1,397	1,860	2,306	2,896	3,355	5,041
	0,129	0,261	0,398	0,543	0,703	0,883	1,100	1,383	1,833	2,262	2,821	3,250	4,781
	0,129	0,260	0,327	0,542	0,700	0,879	1,093	1,372	1,812	2,228	2,764	3,169	4,583
	0,129	0,260	0,396	0,540	0,697	0,876	1,088	1,363	1,796	2,201	2,718	3,106	4,437
	0,128	0,259	0,395	0,539	0,695	0,873	1,083	1,356	1,782	2,179	2,681	3,055	4,318
	0,128	0,259	0,394	0,538	0,694	0,870	1,079	1,350	1,771	2,160	2,650	3,012	4,221
	0,128	0,258	0,393	0,537	0,692	0,868	1,076	1,345	1,761	2,145	2,624	2,977	4,140
	0,128	0,258	0,393	0,536	0,691	0,866	1,074	1,341	1,753	2,131	2,602	2,947	4,073
	0,128	0,258	0,392	0,535	0,690	0,865	1,071	1,337	1,746	2,120	2,583	2,921	4,015
	0,128	0,257	0,392	0,534	0,689	0,863	1,069	1,333	1,740	2,110	2,567	2,898	3,965
	0,127	0,257	0,392	0,534	0,688	0,862	1,067	1,330	1,734	2,101	2,552	2,878	3,922
	0,127	0,257	0,391	0,533	0,688	0,861	1,066	1,328	1,729	2,093	2,539	2,861	3,833
	0,127	0,257	0,391	0,533	0,687	0,860	1,064	1,325	1,725	2,086	2,528	2,845	3,850

Окончание табл. 2

n	В е р о я т н о с т ь a = St (t) = P (|T| > tтабл)
0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1	0,05	0,02	0,01	0,001
	0,127	0,257	0,391	0,532	0,686	0,859	1,063	1,323	1,721	2,080	2,518	2,831	3,819
	0,127	0,256	0,390	0,532	0,686	0,858	1,061	1,321	1,717	2,074	2,508	2,819	3,792
	0,127	0,256	0,390	0,532	0,685	0,868	1,060	1,319	1,714	2,069	2,500	2,807	3,767
	0,127	0,256	0,390	0,531	0,685	0,857	1,059	1,318	1,711	2,064	2,402	2,797	3,745
	0,127	0,256	0,390	0,531	0,684	0,856	1,058	1,316	1,708	2,060	2,485	2,787	3,725
	0,127	0,256	0,390	0,531	0,684	0,856	1,058	1,315	1,706	2,056	2,479	2,779	3,707
	0,127	0,256	0,389	0,531	0,684	0,855	1,057	1,314	1,703	2,052	2,473	2,771	3,690
	0,127	0,256	0,389	0,530	0,683	0,855	1,056	1,313	1,701	2,048	2,467	2,763	3,674
	0,127	0,256	0,389	0,530	0,683	0,854	1,055	1,311	1,699	2,045	2,462	2,756	3,659
	0,127	0,256	0,389	0,530	0,683	0,854	1,055	1,310	1,697	2,042	2,457	2,750	3,646
	0,126	0,255	0,388	0,529	0,681	0,851	1,050	1,303	1,684	2,021	2,423	2,704	3,551
	0,126	0,254	0,387	0,527	0,679	0,848	1,046	1,296	1,671	2,000	2,390	2,660	3,460
	0,126	0,254	0,386	0,526	0,677	0,845	1,041	1,289	1,658	1,980	2,358	2,617	3,373
¥	0,126	0,253	0,385	0,524	0,674	0,842	1,036	1,282	1,645	1,960	2,326	2,576	3,291

Таблица 3

Р а с п р е д е л е н и е П и р с о н а (c²-распределение)

Значения c²_таблдля вероятностей Р (c² > c²_табл)

n	В е р о я т н о с т ь P (c2)
0,999	0,995	0,99	0,98	0,975	0,95	0,90	0,80	0,75	0,70	0,50
	0,00000157	0,0000393	0,000157	0,000628	0,000982	0,00393	0,0158	0,0642	0,102	0,148	0,455
	0,00200	0,0100	0,0201	0,0404	0,0506	0,103	0,211	0,446	0,575	0,713	1,386
	0,0243	0,0717	0,115	0,185	0,216	0,352	0,584	1,005	1,213	1,424	2,366
	0,0908	0,207	0,297	0,429	0,484	0,711	1,064	1,649	1,923	2,195	3,357
	0,210	0,412	0,554	0,752	0,831	1,145	1,610	2,343	2,675	3,000	4,351
	0,381	0,676	0,872	1,134	1,237	1,635	2,204	3,070	3,455	3,828	5,348
	0,598	0,989	1,239	1,564	1,690	2,167	2,833	3,822	4,255	4,671	6,346
	0,857	1,344	1,646	2,032	2,180	2,733	3,490	4,594	5,071	5,527	7,344
	1,152	1,735	2,088	2,532	2,700	3,325	4,168	5,380	5,899	6,393	8,343
	1,479	2,156	2,558	3,059	3,247	3,240	4,865	6,179	6,737	7,267	9,342
	1,834	2,603	3,053	3,609	3,816	4,575	5,578	6,989	7,584	8,148	10,341
	2,214	3,074	3,571	4,178	4,404	5,226	6,304	7,807	8,438	9,034	11,340
	2,617	3,565	4,107	4,765	5,009	5,892	7,042	8,634	9,299	9,926	12,340
	3,041	4,075	4,660	5,368	5,629	6,571	7,790	9,467	10,165	10,821	13,339
	3,483	4,601	5,229	5,985	6,262	7,261	8,547	10,307	11,036	11,721	14,339
	3,942	5,142	5,812	6,614	6,908	7,962	9,312	11,152	11,912	12,624	15,338
	4,416	5,697	6,408	7,255	7,564	8,672	10,085	12,002	12,892	13,531	16,338
	4,905	6,265	7,015	7,906	8,231	9,390	10,865	12,857	13,675	14,440	17,338
	5,407	6,844	7,633	8,567	8,907	10,117	11,651	13,716	14,562	15,352	18,338
	5,921	7,434	8,260	9,237	9,591	10,871	12,443	14,578	15,452	16,266	19,337
	6,447	8,034	8,897	9,915	10,283	11,591	13,240	15,445	16,344	17,182	20,337
	6,983	8,643	9,542	10,600	10,982	12,338	14,041	16,314	17,240	18,101	21,337
	7,529	9,260	10,196	11,293	11,688	13,091	14,848	17,187	18,137	19,021	22,337
	8,035	9,886	10,856	11,992	12,401	13,848	15,659	18,062	19,037	19,943	23,337
	8,649	10,520	11,524	12,697	13,120	14,611	16,173	18,940	19,939	20,887	24,337
	9,222	11,160	12,198	13,409	13,844	15,379	17,292	19,820	20,843	21,792	25,336
	9,803	11,808	12,879	14,125	14,573	16,151	18,114	20,703	21,749	22,719	26,136
	10,391	12,461	13,565	14,847	15,308	16,928	18,937	21,588	22,657	23,617	27,336
	10,986	13,121	14,256	15,574	16,047	17,708	19,768	22,475	23,567	24,577	28,336
	11,588	13,787	14,953	16,306	16,791	18,493	20,599	23,364	24,478	25,508	29,336

Окончание табл. 3

n	Вероятность P (c2)
0,30	0,25	0,20	0,10	0,05	0,025	0,02	0,01	0,005	0,001
	1,074	1,323	1,642	2,706	3,841	5,024	5,412	6,635	7,879	10,827
	2,408	2,773	3,219	4,605	5,991	7,378	7,824	9,210	10,597	13,815
	3,665	4,108	4,642	6,251	7,815	9,348	9,837	11,345	12,838	16,268
	4,878	5,385	5,989	7,779	9,488	11,143	11,668	13,277	14,860	18,465
	6,064	6,626	7,289	9,236	11,070	12,839	13,388	15,086	16,750	20,517
	7,231	7,841	8,558	10,645	12,592	14,449	15,033	16,812	18,548	22,457
	8,383	9,037	9,803	12,017	14,067	16,013	16,622	18,475	20,278	24,322
	9,524	10,219	11,030	13,362	15,507	17,535	18,168	20,090	21,955	26,125
	10,656	11,389	12,242	14,684	16,919	19,023	19,679	21,666	23,589	27,877
	11,781	12,549	13,412	15,987	18,307	20,483	21,161	23,209	25,188	29,588
	12,899	13,701	14,631	17,275	19,675	21,920	22,618	24,725	26,757	31,264
	14,011	14,845	15,812	18,549	21,026	23,337	24,054	26,217	28,300	32,909
	15,119	15,984	16,985	19,812	22,362	24,736	25,472	27,688	29,819	34,528
	16,222	17,117	18,151	21,064	23,685	26,119	26,873	29,141	31,319	36,123
	17,322	18,245	19,311	22,307	24,996	27,488	28,259	30,578	32,801	37,697
	18,418	19,369	20,465	23,542	26,296	28,845	29,633	32,000	34,267	39,252
	19,511	20,489	21,615	24,769	27,587	30,191	30,995	33,409	35,718	40,790
	20,601	21,605	22,760	25,989	28,869	31,526	32,346	34,805	37,156	42,312
	21,689	22,718	23,900	27,204	30,144	32,852	33,687	36,191	38,582	43,820
	22,775	23,828	25,038	28,412	31,410	34,170	35,020	37,566	39,997	45,315
	23,858	24,935	26,171	29,615	32,671	35,479	36,343	38,932	41,401	46,797
	24,939	26,039	27,301	30,813	33,924	36,781	37,659	40,289	42,796	48,268
	26,018	27,141	28,429	32,007	35,172	38,076	38,968	41,638	44,181	49,728
	27,096	28,241	29,553	33,196	36,415	39,364	40,270	42,980	45,558	51,170
	28,172	29,339	30,675	34,382	37,652	40,046	41,566	44,314	46,928	52,620
	29,246	30,434	31,795	35,563	38,885	41,923	42,856	45,642	48,290	54,052
	30,319	31,528	32,912	36,741	40,113	43,194	44,140	46,963	49,645	55,476
	31,391	32,620	34,027	37,916	41,337	44,461	45,419	48,278	50,993	56,893
	32,461	33,711	35,139	39,087	42,557	45,722	46,693	49,588	52,336	58,302
	33,530	34,800	36,250	40,256	43,773	46,979	47,962	50,892	53,672	59,703

Таблица 4

Р а с п р е д е л е н и е Ф и ш е р а - С н е д е к о р а (F-распределение)