Кинетическая энергия тела, вращающего вокруг неподвижной оси, равна , где - угловая скорость, а - момент инерции относительно оси вращения. Зная это, решить задачи 23-30.
КОНТРОЛЬНАЯ РАБОТА № 5
Рассмотрим варианты решения заданий контрольной работы № 5.
Образцы выполнения заданий № 171-200.
1. Вычислить определенный интеграл 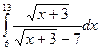 .
.
Решение.
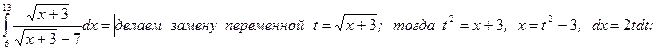
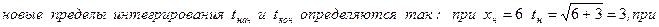
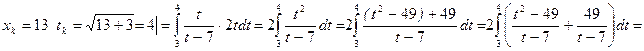
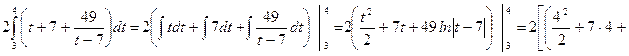
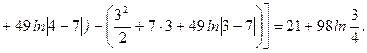
2. Вычислить несобственный интеграл  или доказать его расходимость.
или доказать его расходимость.
Решение.
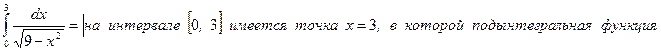
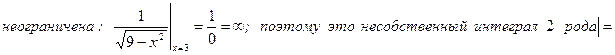
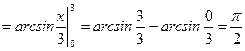 .
.
3. Вычислить площадь, заключенную между линиями 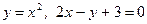 . Найдем абсциссы точек пересечения этих линий, решив систему
. Найдем абсциссы точек пересечения этих линий, решив систему 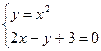 .
.
Получим 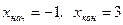 (рис. 1).
(рис. 1).
 Искомая площадь равна
Искомая площадь равна 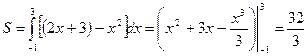 .
.
 |
4. Вычислить площадь фигуры, ограниченной линией 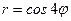 в полярных координатах.
в полярных координатах.
Решение.
Графиком функции 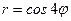 является четырехлепестковая роза. Искомая площадь
является четырехлепестковая роза. Искомая площадь 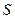 равна
равна 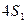 , где
, где 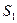 - площадь одного лепестка.
- площадь одного лепестка.
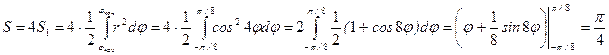 .
.
5. Найти длину линии 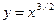 при
при 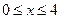 .
.
Решение.
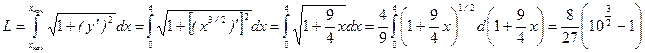 .
.
6. Найти длину одной арки циклоиды, заданной параметрически уравнениями 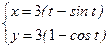 .
.
Когда параметр 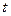 изменяется от
изменяется от 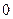 до
до 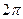 , получается одна из арок (рис.2).
, получается одна из арок (рис.2).
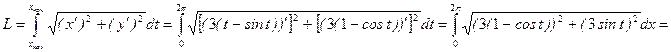
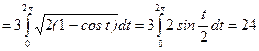 .
.
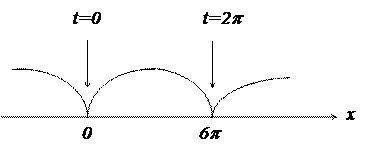 |
 |
7. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 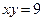 ,
, 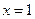 ,
, 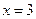 .
.
Решение.
 Когда фигура, изображенная на рисунке 3, вращается вокруг оси Ох, то получится тело, объем которого
Когда фигура, изображенная на рисунке 3, вращается вокруг оси Ох, то получится тело, объем которого 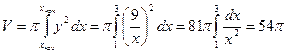 .
.
Рисунок 3
КОНТРОЛЬНАЯ РАБОТА № 6
Рассмотрим варианты решения заданий контрольной работы № 6.
Образец выполнения заданий № 201-210
Изменить порядок интегрирования в интеграле 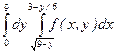 . Область интегрирования изобразить на чертеже.
. Область интегрирования изобразить на чертеже.
Решение.
Выпишем из условия задачи область изменения переменных
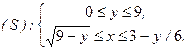
Изобразим эту область (на рисунке 4 она заштрихована).
При измерении порядка интегрирования область 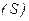 разобъется на две части
разобъется на две части
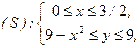
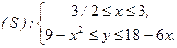
Отсюда 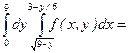
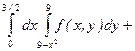
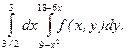
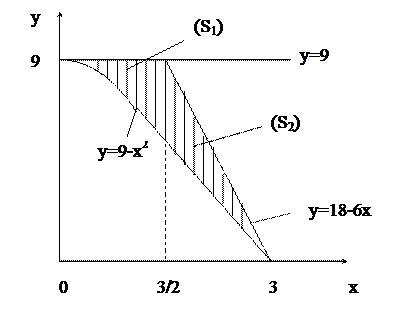 |
Рисунок 4
Образец выполнения заданий № 211-220.
Вычислить объем тела, ограниченного поверхностями 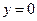 ,
, 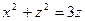 ,
, 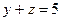 .
.
Решение.
Сделаем чертеж данного тела (рис. 5). Он показывает, что проекций этого тела на плоскость 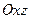 является круг
является круг 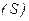 , поэтому объем можно вычислить по формуле
, поэтому объем можно вычислить по формуле
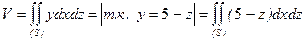 .
.
Рисунок 6 показывает, что область 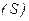 задается неравенствами
задается неравенствами
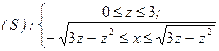 ,
,
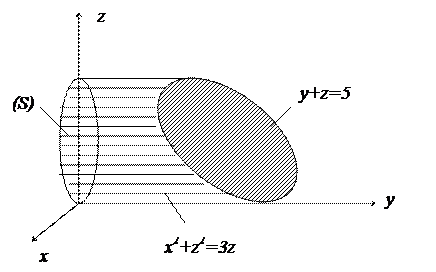 |
Рисунок 5
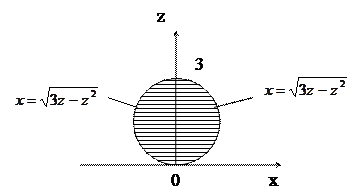 |
Рисунок 6
поэтому
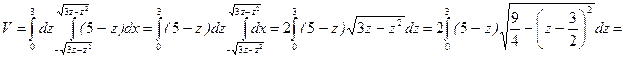
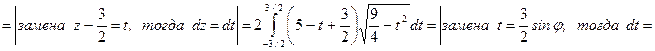
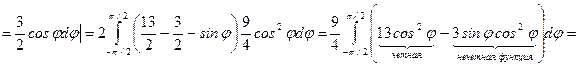
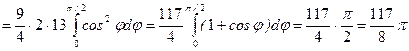 .
.
Образец выполнения задания № 22
а) Найти площадь фигуры, ограниченной замкнутой линией 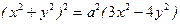 ,
, 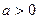 .
.
Решение.
Уравнение линии упростится, если перейти к полярным координатам 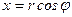 ,
, 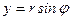 (
( 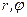 - полярные координаты,
- полярные координаты, 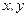 - декартовы координаты). Подставив в уравнение линии, получим
- декартовы координаты). Подставив в уравнение линии, получим 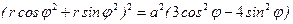 ,
, 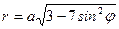 - уравнение линии в полярных координатах.
- уравнение линии в полярных координатах.
Найдем ОДЗ: 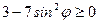 ,
, 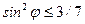 ,
, 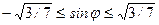 ,
,
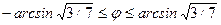 и
и 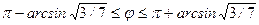 .
.
Вследствие симметрии фигуры можно найти площадь заштрихованной части и умножить на 4 (рис. 7).
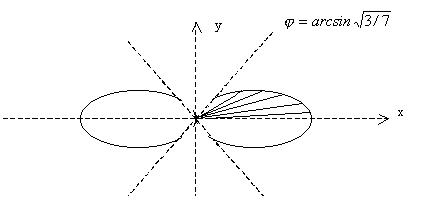 |
Рисунок 7
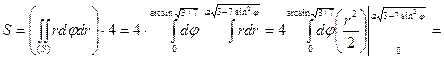
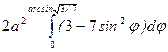
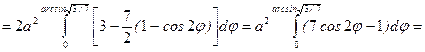
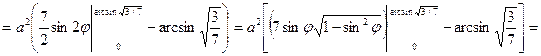
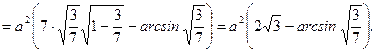
б) вычислить двойной интеграл, используя полярные координаты 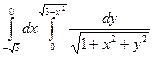 .
.
Решение
Область интегрирования задается интервалами:
- 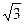 ≤x≤0, 0≤y≤
≤x≤0, 0≤y≤ 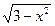
И представляет собой четверть окружности с центром в начале координат и радиуса 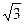 , расположенной во второй четверти.
, расположенной во второй четверти.
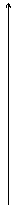 y=(3-x2)1/2
y=(3-x2)1/2


 y=(3-x2)1/2
y=(3-x2)1/2 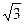
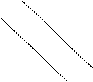
 D
D

 0
0
Переходим к полярным координатам по формулам
x=rcosφ, y=rsinφ (r,φ-полярные координаты; x,y- декартовые координаты).
Тогда область интегрирования представляется в виде:
0≤r≤ 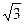 , π/2≤φ≤π
, π/2≤φ≤π
Заданный двойной интеграл в полярных координатах примет вид:
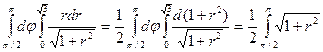
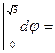
= 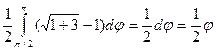
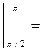
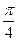 .
.
Ответ: 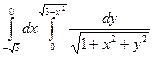 =
= 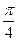 .
.
Образцы выполнения заданий № 231-240
1. Найти массу полушара 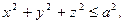
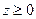 , если плотность в каждой точке
, если плотность в каждой точке 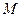 обратно пропорциональна расстоянию от
обратно пропорциональна расстоянию от 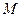 до начала координат.
до начала координат.
Решение.
Сделаем чертеж (рис. 8). Внутри тела возьмем произвольную точку 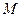 . Тогда
. Тогда
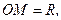
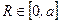 .
.
По условию плотность равна 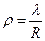 , где
, где 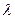 - коэффициент пропорциональности. Тогда масса бесконечно малого кусочка объема
- коэффициент пропорциональности. Тогда масса бесконечно малого кусочка объема 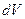 равна
равна 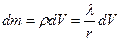 , а масса всего тела
, а масса всего тела 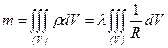 .
.
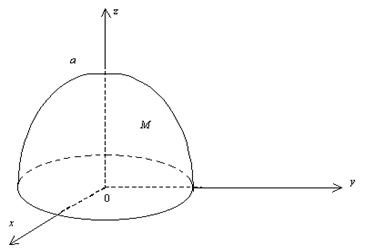 |
Рисунок 8
В сферических координатах 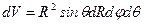 , а объем
, а объем 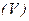 , показанный на рисунке, задается неравенствами
, показанный на рисунке, задается неравенствами 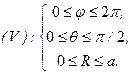
Поэтому 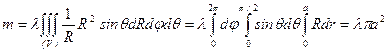 .
.
2. Найти координаты центра тяжести полушара, данного в предыдущей задаче.
Решение.
Координаты центра тяжести тела находятся по формулам
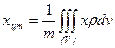 ,
,  ,
, 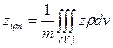 ,
,
в которых 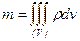 - масса тела.
- масса тела.
Ось Оz является осью симметрии полушара, поэтому центр тяжести лежит на оси Оz, т.е. 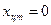 ,
, 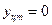 .
.
Масса полушара найдена в предыдущей задаче, 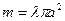 . Найдем оставшиеся тройные интеграл.
. Найдем оставшиеся тройные интеграл.
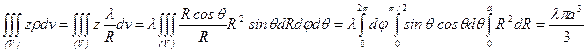 ,
,
поэтому 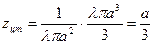 .
.
Ответ: 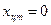 ,
, 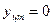 ,
, 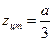 .
.
3. Найти момент инерции 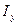 относительно оси
относительно оси 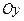 полушара, заданного в предыдущей задаче.
полушара, заданного в предыдущей задаче.
Решение.
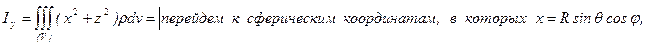
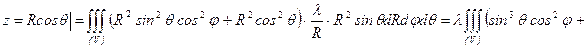
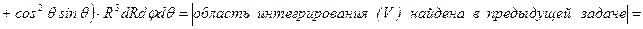
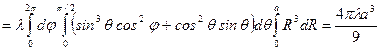 .
.
Образец выполнения задания № 241-250
Вычислить криволинейный интеграл 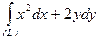 , где
, где 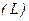 - четверть окружности
- четверть окружности 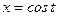 ,
, 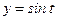 между начальной точкой
между начальной точкой 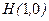 и конечной
и конечной 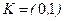 .
.
Решение.
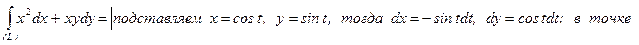
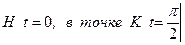
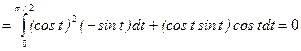 .
.
Образец выполнения задания № 251-260
Дана функция 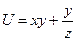 и вектор
и вектор 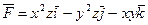 . Требуется найти: 1) направление наибольшего возрастания функции в точке
. Требуется найти: 1) направление наибольшего возрастания функции в точке 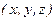 и скорость возрастания функции в этом направлении; 2)
и скорость возрастания функции в этом направлении; 2) 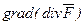 ; 3)
; 3) 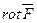 .
.
Решение. 1) Направление наибольшего возрастания функции задается вектором 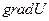 :
:
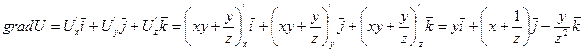 .
.
Скорость возрастания функции в этом направлении равна
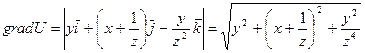 .
.
2) 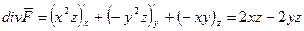 , отсюда
, отсюда
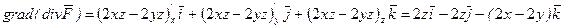 .
.
3) 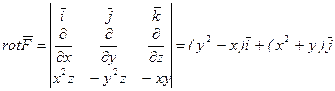 .
.
Образец выполнения задания № 261-270
Дан вектор 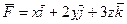 и плоскость (р):
и плоскость (р): 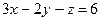 . Плоскость (р) вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется: 1) по формуле Остроградского найти поток
. Плоскость (р) вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется: 1) по формуле Остроградского найти поток 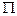 вектора
вектора 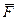 через поверхность пирамиды в направлении внешней нормали; 2) найти циркуляцию
через поверхность пирамиды в направлении внешней нормали; 2) найти циркуляцию 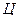 вектора
вектора 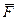 вдоль линии пересечения плоскости (р) с координатными плоскостями непосредственно и по формуле Стокса, принимая в формуле Стокса за поверхность по которой ведется интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом то направление обхода линии интегрирования следует считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть из начала координат.
вдоль линии пересечения плоскости (р) с координатными плоскостями непосредственно и по формуле Стокса, принимая в формуле Стокса за поверхность по которой ведется интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом то направление обхода линии интегрирования следует считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть из начала координат.
Решение.
Плоскость 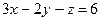 проходит через точки
проходит через точки 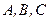 , показанные на рисунке.
, показанные на рисунке.
1) Поток через замкнутую поверхность 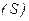 вычисляется по формуле Остроградского
вычисляется по формуле Остроградского
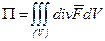 ,
,
в которой 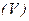 - область внутри
- область внутри 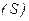 . В нашей задаче
. В нашей задаче 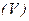 - пирамида
- пирамида 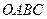 , которую можно задавать системой неравенств
, которую можно задавать системой неравенств 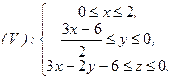
Вычислим дивергенцию вектора 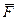 :
:
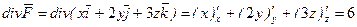 .
.
Теперь вычислим поток:
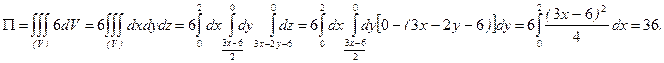 2) По условию задачи, требуется вычислить циркуляцию по контуру
2) По условию задачи, требуется вычислить циркуляцию по контуру 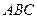 двумя способами.
двумя способами.
а) Непосредственно.
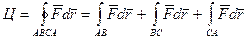 .
.
В нашей задаче 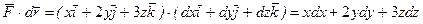 . Вычислим отдельно каждый интеграл.
. Вычислим отдельно каждый интеграл.
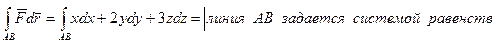
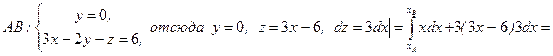
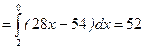 .
.
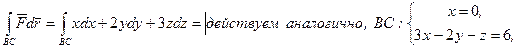
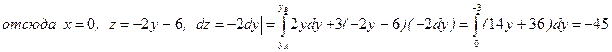 .
.
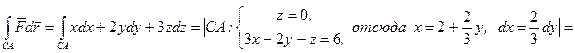
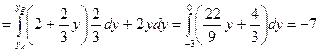 .
.
Следовательно 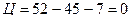 .
.
б) По формуле Стокса циркуляция вычисляется так 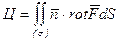 , где
, где 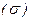 - грань
- грань 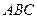 пирамиды,
пирамиды, 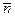 - единичный нормальный вектор к этой грани, согласованный с направлением обхода этой грани. Грань
- единичный нормальный вектор к этой грани, согласованный с направлением обхода этой грани. Грань 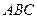 имеет уравнение
имеет уравнение 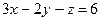 или
или 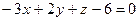 ; нормальный вектор имеет координаты
; нормальный вектор имеет координаты 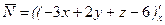 ,
, 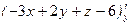 ,
, 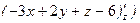
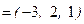 ; его длина
; его длина 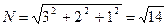 .
.
Отсюда получаем единичный вектор 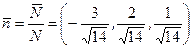 .
.
Вычислим ротор вектора 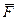
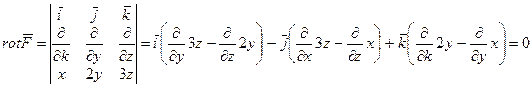 .
.
Отсюда 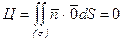 .
.
ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ
КОНТРОЛЬНАЯ РАБОТА № 4
НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
Задание 16. Найти указанные неопределенные интегралы. Результаты, полученные при решении задач 1-20, проверить дифференцированием.
1. а) 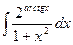 ; 2. а)
; 2. а) 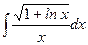 ;
;
б) 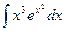 ; б)
; б) 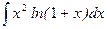 ;
;
в) 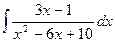 . в)
. в) 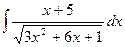 .
.
3. а) 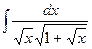 ; 4. а)
; 4. а) 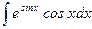 ;
;
б) 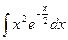 ; б)
; б) 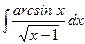 ;
;
в) 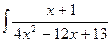 . в)
. в) 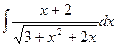 .
.
5. а) 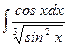 ; 6. а)
; 6. а) 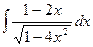 ;
;
б) 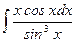 ; б)
; б) 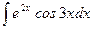 ;
;
в) 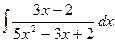 . в)
. в) 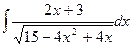 .
.
7. а) 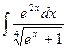 ; 8. а)
; 8. а) 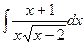 ;
;
б) 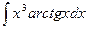 ; б)
; б) 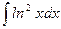 ;
;
в) 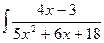 . в)
. в) 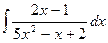 .
.
9. а) 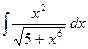 ; 10. а)
; 10. а) 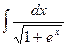 ;
;
б) 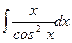 ; б)
; б) 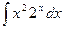 ;
;
в) 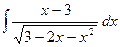 . в)
. в) 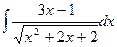 .
.
11. а) 
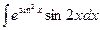 ; 12. а)
; 12. а) 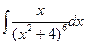 .
.
б) 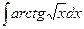 ; б)
; б) 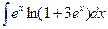 ;
;
в) 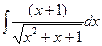 . в)
. в) 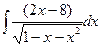 .
.
13. а) 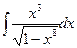 . 14. а)
. 14. а) 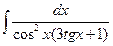
б) 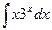 ; б)
; б) 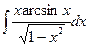
в) 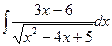 в)
в) 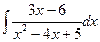
15. а) 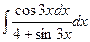 16. а)
16. а) 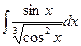
б) 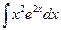 б)
б) 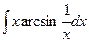
в) 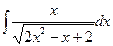 в)
в) 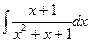
17. а) 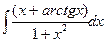 18. а)
18. а) 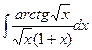
б) 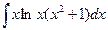 б)
б) 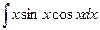
в) 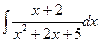 в)
в) 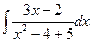
19. а) 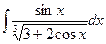 в)
в) 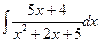
б) 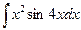
20. а) 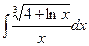 в)
в) 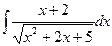
б) 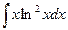
21. а) 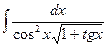 ; 22. а)
; 22. а) 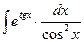
б) 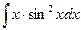 б)
б) 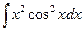
в) 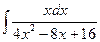 . в)
. в) 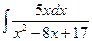 .
.
23. а) 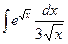 ; 24. а)
; 24. а) 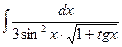 ;
;
б) 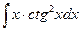 ; б)
; б) 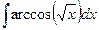 ;
;
в) 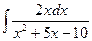 . в)
. в) 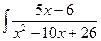 .
.
25. а) 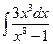 ; 26. а)
; 26. а) 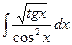 ;
;
б) 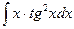 ; б)
; б) 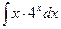 ;
;
в) 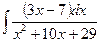 . в)
. в) 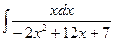 .
.
27. а) 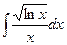 ; 28. а)
; 28. а) 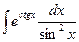 ;
;
б) 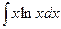 ; б)
; б) 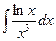 ;
;
в) 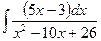 . в)
. в) 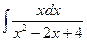 .
.
29. а) 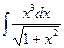 ; 30. а)
; 30. а) 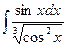 ;
;
б) 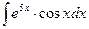 ; б)
; б) 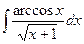 ;
;
в) 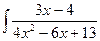 . в)
. в) 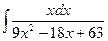 .
.
Задание 17. Вычислить неопределенные интегралы
1. а) 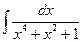 16. а)
16. а) 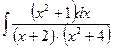
б) 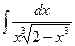 б)
б) 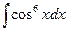
в) 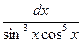 в)
в) 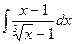
2. а) 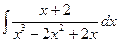 17. а)
17. а) 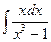
б) 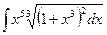 б)
б) 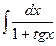
в) 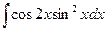 в)
в) 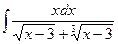
3. а) 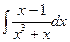 18. а)
18. а) 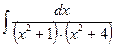
б) 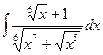 б)
б) 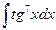
в) 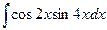 в)
в) 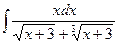
4. а) 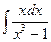 19. а)
19. а) 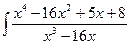
б) 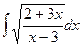 б)
б) 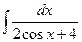
в) 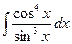 в)
в) 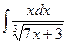
5. а) 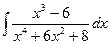 20. а)
20. а) 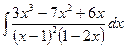
б) 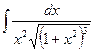 б)
б) 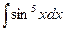
в) 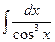 в)
в) 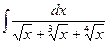
6. а) 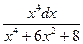 21. а)
21. а) 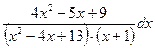
б) 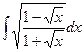 б)
б) 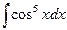
в) 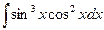 в)
в) 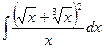
7. а) 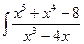 22. а)
22. а) 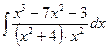
б) 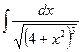 б)
б) 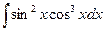
в) 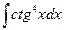 в)
в) 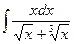
8. а) 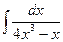 23. а)
23. а) 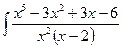
б) 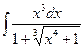 б)
б) 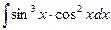
в) 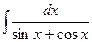 в)
в) 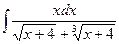
9. а) 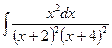 24. а)
24. а) 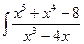
б) 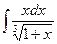 б)
б) 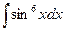
в) 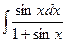 в)
в) 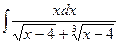
10. а) 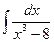 25. а)
25. а) 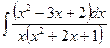
б) 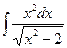 б)
б) 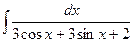
в) 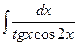 в)
в) 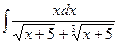
11. а) 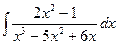 26. а)
26. а) 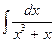
б) 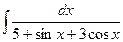 б)
б) 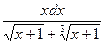
в) 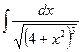 в)
в) 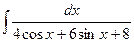
12. а) 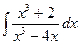 27. а)
27. а) 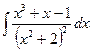
б) 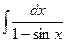 б)
б) 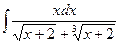
в) 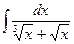 в)
в) 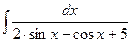
13. а) 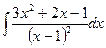 28. а)
28. а) 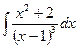
б) 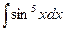 б)
б) 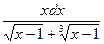
в) 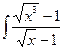 в)
в) 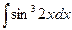
14. а) 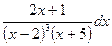 29. а)
29. а) 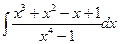
б) 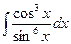 б)
б) 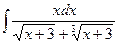
в) 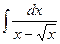 в)
в) 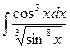
15. а) 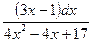 30. а)
30. а) 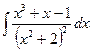
б) 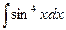 б)
б) 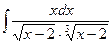
в) 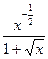 в)
в) 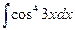
КОНТРОЛЬНАЯ РАБОТА № 5
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
Задание 18. В задачах 1-20 вычислить указанные определенные интегралы.
1. 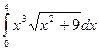 . 2.
. 2. 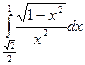 .
.
3. 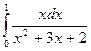 . 4.
. 4. 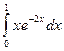 .
.
5. 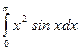 . 6.
. 6. 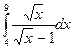 .
.
7. 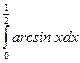 . 8.
. 8. 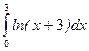 .
.
9. 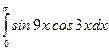 . 10.
. 10. 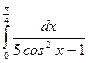 .
.
Вычислить несобственный интеграл или доказать его расходимость.
11. 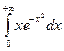 . 15.
. 15. 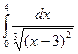 .
.
12. 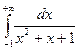 . 16.
. 16. 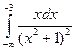 .
.
13. 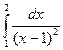 . 17.
. 17. 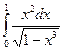 .
.
14. 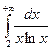 . 18.
. 18. 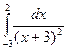
19. 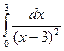 20.
20. 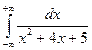
21. 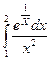 22.
22. 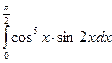
23. 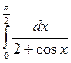 24.
24. 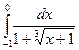
25. 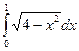 26.
26. 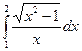
27. 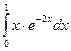 28.
28. 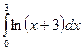
29. 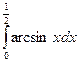 30.
30. 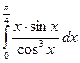
Задание 19. В задачах 1-20 найти площадь фигуры, ограниченной линиями, сделать чертеж.
1. x-2y+6=0, x=-2, x=4, y=0.
2. y=x2+2, x=-1, x=2, y=0
3. xy=6, y=7-x
4. y=-x2-1, x=1, x=4, y=0
5. y=x2-6x, y=0
6. y=x3, y=x, y=2x
7. y=-x2+4, y=x2-2x
8. y=x2+2x, y=0
9. y=-2x2-2, x=-1, x=2, y=0
10. y=-x2+5, y=x+3
11. y=x2, y=2x
12. y=x2, y=1-x2
13. y=x2-x-6, y=0
14. y=x2+2x+1, y=0, x=-3, x=2
15. 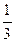 x2+3x+4, y=
x2+3x+4, y= 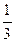 x+1, x=-1, x=2
x+1, x=-1, x=2
16. - 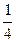 x2+2x, y=
x2+2x, y= 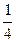 x+
x+ 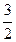
17. 2x+y-2=0, x=-2, x=0
18. 2x+y-2=0, x=-4, x=0
19. x2+y2=4, x=0, x=2
20. (x+1)2+y2=1, (y≥0), x=0, x=2
21. Вычислить площадь фигуры ограниченной гиперболой 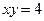 и прямой
и прямой 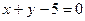 .
.
22. Вычислить объем тела, образованного вращением вокруг оси 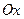 фигуры, ограниченной параболами
фигуры, ограниченной параболами 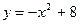 и
и 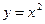 .
.
23. Вычислить объем тела, образованного вращением вокруг оси 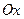 фигуры, ограниченной окружностью
фигуры, ограниченной окружностью 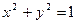 , параболой
, параболой 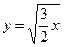 и осью
и осью 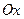 .
.
24. Вычислить площадь фигуры, ограниченной параболами 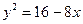 и
и 
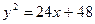 .
.
25. Фигуры ограничена линией, заданной уравнением 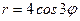 в полярных координатах. Вычислить площадь той ее части, которая расположена вне круга с центром в полюсе и радиусом
в полярных координатах. Вычислить площадь той ее части, которая расположена вне круга с центром в полюсе и радиусом 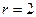 .
.
26. Вычислить площадь фигуры, ограниченной параболой 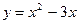 и прямой
и прямой 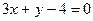 .
.
27. Вычислить площадь фигуры, ограниченной линией 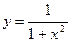 и параболой
и параболой 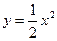 .
.
28. Вычислить длину дуги параболы 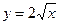
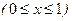 .
.
29. Вычислить длину дуги кривой, заданной параметрическими уравнениями 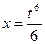 ,
, 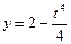 , между точками ее пересечения с осями координат.
, между точками ее пересечения с осями координат.
30. Вычислить длину полукубической параболы 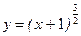 , если
, если 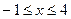 .
.
Задание 20. Решить физические задачи с помощью определенного интеграла.
1. Определить координаты центра тяжести однородной плоской фигуры, ограниченной параболами 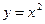 и
и 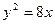 .
.
2. Определить координаты центра тяжести однородной плоской фигуры, ограниченной осями координат и параболой 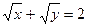 .
.
3. Найти координаты центра тяжести полукруга, ограниченного осью абсцисс и полуокружностью 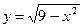 .
.
4. Вычислить работу, которую необходимо затратить, чтобы выкачать воду из канонического сосуда, обращенного вершиной вниз, радиус основания которого равен 2 м и высота 6 м.
5. Цилиндрический сосуд, площадь поперечного сечения которого 20 см2, а высота 60 см, наполнен газом под атмосферным давлением (1,033 кГ/см2). Пользуясь законом Бойля – Мариотта, определить работу, затрачиваемую на изотермическое сжатие газа, если поршень, закрывающий цилиндр, будет вдвинут на 40 см вовнутрь цилиндра.
6. Вертикальная плотина имеет форму трапеции. Вычислить силу давления воды на плотину, если известно, что верхнее основание плотины 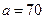 м, нижнее основание
м, нижнее основание 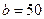 м, а высота
м, а высота 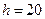 м.
м.
7. Сжатие пружины пропорционально приложенной силе. Вычислить работу силы при сжатии пружины на 8 см, если для сжатия ее на 1 см требуется сила в 0,05 н.
8. Деревянный поплавок цилиндрический формы, площадь основания которого 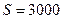 см2, а высота
см2, а высота 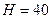 см, плавает на поверхности воды. Удельный вес дерева
см, плавает на поверхности воды. Удельный вес дерева 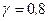 Г/см3. Вычислить, какую работу нужно затратить, чтобы вытащить поплавок из воды.
Г/см3. Вычислить, какую работу нужно затратить, чтобы вытащить поплавок из воды.
9. Тело движется прямолинейно по закону 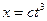 , где
, где 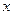 - длина пути, проходимого за время
- длина пути, проходимого за время 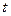 ,
, 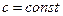 . Сопротивление среды пропорционально квадрату скорости, причем коэффициент пропорциональности равен
. Сопротивление среды пропорционально квадрату скорости, причем коэффициент пропорциональности равен 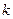 . Найти работу, производимую сопротивлением при передвижении тела от точки
. Найти работу, производимую сопротивлением при передвижении тела от точки 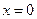 , до точки
, до точки 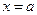 .
.
10. Найти проекции на оси координат силы, с которой материальная полуокружность массы 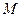 и радиуса
и радиуса 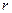 действует на материальную точку
действует на материальную точку 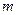 находящуюся в ее центре (две материальные точки притягиваются с силой, модуль которой
находящуюся в ее центре (две материальные точки притягиваются с силой, модуль которой 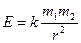 ). Начало координат следует взять в центре полуокружности, а оси координат направить соответственно по горизонтальному и вертикальному диаметрам.
). Начало координат следует взять в центре полуокружности, а оси координат направить соответственно по горизонтальному и вертикальному диаметрам.
Сила взаимодействия двух точечных масс определяется по формуле , где и - мысы точек, - расстояние между ними, а - коэффициент пропорциональности, равный (закон Ньютона). Учитывая это, решить задачи 11-22 (Предполагается, что плотность постоянна).
11. Стержень АВ, длина которого 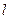 , масса
, масса 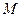 , притягивает точку С массы
, притягивает точку С массы 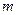 , которая лежит на его продолжении на расстоянии
, которая лежит на его продолжении на расстоянии 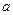 от ближайшего конца В стержня. Найти силу взаимодействия стержня и точки. Какую точечную массу нужно поместить в А, для того чтобы она действовала на С с той же силой, что и стержень АВ? Какую работу совершит сила притяжения, когда точка, отстоявшая от стержня на расстоянии
от ближайшего конца В стержня. Найти силу взаимодействия стержня и точки. Какую точечную массу нужно поместить в А, для того чтобы она действовала на С с той же силой, что и стержень АВ? Какую работу совершит сила притяжения, когда точка, отстоявшая от стержня на расстоянии 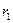 , приблизится к нему на расстоянии
, приблизится к нему на расстоянии 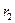 , двигаясь вдоль прямой, составляющей продолжение стержня?
, двигаясь вдоль прямой, составляющей продолжение стержня?
12. С какой силой полукольцо радиуса 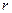 и массы
и массы 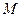 действует на материальную точку массы
действует на материальную точку массы 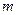 , находящуюся в его центре?
, находящуюся в его центре?
13. С какой силой проволочное кольцо массы 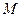 , радиуса
, радиуса 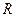 действует на материальную точку
действует на материальную точку 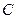 массы
массы 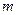 , лежащую на прямой, проходящей через центр кольца перпендикулярно к его плоскости. Расстояние от точки до центра кольца равно
, лежащую на прямой, проходящей через центр кольца перпендикулярно к его плоскости. Расстояние от точки до центра кольца равно 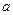 . Какую работу совершит сила притяжения при перемещении точки из бесконечности в центр кольца?
. Какую работу совершит сила притяжения при перемещении точки из бесконечности в центр кольца?
14. Используя результат предыдущей задачи, вычислить с какой силой плоский диск, радиус которого равен 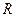 , масса -
, масса - 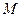 , действует на материальную точку массы
, действует на материальную точку массы 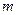 , которая лежит на его оси на расстоянии
, которая лежит на его оси на расстоянии 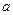 от центра.
от центра.
15. Радиусы оснований усеченного прямого круглого конуса равны 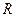 и
и 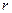 , высота
, высота 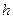 , плотность
, плотность 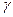 . С какой силой действует он на материальную точку массы
. С какой силой действует он на материальную точку массы 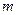 , помещенную в его вершин?
, помещенную в его вершин?
16. Два одинаковых стержня (длиной 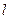 и массы
и массы 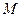 каждый) лежат на одной прямой на расстоянии
каждый) лежат на одной прямой на расстоянии 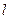 один от другого. Подсчитать силу взаимного притяжения.
один от другого. Подсчитать силу взаимного притяжения.
17. Капля с начальной массой 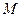 падает под действием силы тяжести и равномерно испаряется, теряя ежесекундно массу, равную
падает под действием силы тяжести и равномерно испаряется, теряя ежесекундно массу, равную 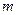 . Какова работа силы тяжести за время от начала движения до полного испарения капли? (Сопротивлением воздуха пренебрегаем.)
. Какова работа силы тяжести за время от начала движения до полного испарения капли? (Сопротивлением воздуха пренебрегаем.)
18. Какую работу нужно произвести, чтобы насыпать кучу песка в форме усеченного конуса высоты 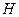 , имеющего радиусы оснований
, имеющего радиусы оснований 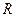 и
и 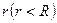 ? Удельный вес равен
? Удельный вес равен 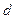 (песок поднимает с поверхности земли, на которой покоится большее основание конуса).
(песок поднимает с поверхности земли, на которой покоится большее основание конуса).
19. Вычислить работу, которую нужно затратить, чтобы выкачать жидкость удельного веса 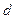 из резервуара, имеющего форму обращенного вершиной вниз конуса, высота которого равна
из резервуара, имеющего форму обращенного вершиной вниз конуса, высота которого равна 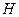 , а радиус основания
, а радиус основания 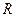 . Как изменится результат, если конус будет обращен вершиной кверху?
. Как изменится результат, если конус будет обращен вершиной кверху?
20. Вычислить работу, которую необходимо затратить, чтобы выкачать воду, наполняющую полусферический резервуар радиуса 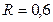 м.
м.
21. Котел имеет форму параболоида вращения (рис 1.). Радиус основания 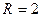 м., глубина котла
м., глубина котла 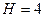 м. Он наполнен жидкостью, удельный вес которой
м. Он наполнен жидкостью, удельный вес которой 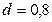 Г/см3. Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
Г/см3. Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла.
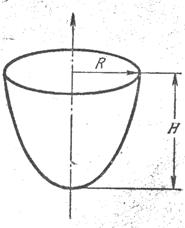 Рис. 1
Рис. 1
22. Найти работу, которую нужно затратить, чтобы выкачать воду из цистерны, которая имеет следующие размеры (рис. 2): 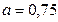 м.,
м., 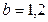 м.,
м., 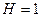 м. Боковая поверхность цистерны – параболический цилиндр.
м. Боковая поверхность цистерны – параболический цилиндр.
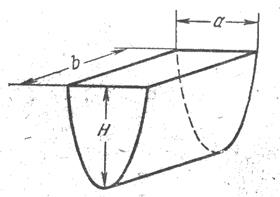 Рис. 2
Рис. 2
Кинетическая энергия тела, вращающего вокруг неподвижной оси, равна , где - угловая скорость, а - момент инерции относительно оси вращения. Зная это, решить задачи 23-30.
23. Стержень АВ (рис. 3) вращается в горизонтальной плоскости вокруг оси ОО’ c угловой скоростью 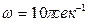 . Поперечное сечение стержня
. Поперечное сечение стержня 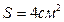 , длина его
, длина его 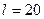 см, плотность материала, из которого он изготовлен,
см, плотность материала, из которого он изготовлен, 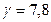 г/см3. Найти кинетическую энергию стержня.
г/см3. Найти кинетическую энергию стержня.
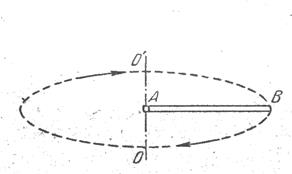 Рис. 3
Рис. 3
24. Прямоугольная пластинка, стороны которой 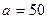 см и
см и 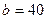 см, вращается постоянной угловой скоростью
см, вращается постоянной угловой скоростью 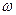 , равной
, равной 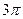 сек-1, вокруг стороны
сек-1, вокруг стороны 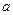 . Найти кинетическую энергию пластинки. Толщина пластинки
. Найти кинетическую энергию пластинки. Толщина пластинки 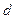 равна 0,3 см, плотность
равна 0,3 см, плотность 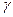 материала, из которого сделана пластинка, равна 8 г/см3.
материала, из которого сделана пластинка, равна 8 г/см3.
