Нүкте қозғалысының берілу тәсілдері

Нүкте және қатты дене кинематикасы

Кинематикаға кіріспе

Теориялық механиканың кинематика бөлімінде денеге әсер ететін күштер есепке алынбаған жағдайдағы механикалық қозғалыс қарастырылады. Кинематика “Кинема” (қозғалыс)” деген грек сөзінін алынған. Теориялық механиканың бұл бөлімінде денелер қозғалыстары, күштерге тәуелсіз, таза геометриялық тұрғыдан қарастырылады. Мұнда қаралатын негізгі мәселелер: а) дененің берілген қозғалысын математикалық формулаларды және графиктер мен кестелерді қолдана отырып сипаттау; б) осы қозғалысты сипаттайтын кинематикалық шамаларды табу. Кинематикаға арнайы енгізілген ұғымдар мен шамалар бар. Олар: нүкте, абсолют қатты дене, санақ жүйесі, траектория мен жол, орын ауыстыру, жылдамдық, үдеу, айналу бұрышы, бұрыштық жылдамдық, бұрыштық үдеу шамалары. Осы ұғымдарды және кинематикалық шамаларды пайдалана отырып, механикалық қозғалыстарын уақыт t-ға тәуелділіктерін өрнектейтін теңдеулерді құру – кинематиканың негізгі мақсатына жатады.

Тек ұзындық бірлігі L және уақыт бірлігі t мен өрнектелінетін шамаларды кинематикалық шамалар деп айтамыз.

Қозғалыстағы дене уақыт өтуіне байланысты басқа денелерге қарағандағы кеңістіктегі орнын өзгертіп отырады, сондықтан оның кеңістіктегі орнын немесе қозғалысын шартты түрде қозғалмайды деп алынған , кез келген бір екінші қатты денемен салыстырып қарау арқылы ғана анықтауға болады. Берілген дененің қозғалысын салыстыру үшін таңдап алынған екінші дене санақ денесі деп аталады. Оны таңдау қарастырылып отырған есептің шешімін табу ыңғайына сәйкес орындалады. Таңдап алынған санақ денесіне координаттар жүйесі бекітіліп алынады. Күн жүйесінің массалар центрінде жатып, өстері қозғалмайтын жұлдыздарға бағытталған координаттар жүйесі негізгі немесе инерциялық координаттар жүйесі деп аталады.

Нүкте кинематикасы

Нүкте қозғалысының берілу тәсілдері

Нүкте қозғалысының заңын анықтаудың немесе қозғалыс теңдеулерін құрудың үш тәсілі бар.

2.1-сурет

1. Табиғи тәсіл. Нүкте қозғалысының берілуінің үш тәсілінің бірі - табиғи тәсіл. Нүкте қозғалысының берілуінің табиғи тәсілінде нүктенің кез келген бір санақ жүйесіне қатысты траекториясы беріледі. Одан кейін, оның бойынан қандайда болсын бір нүкте -ді доға ұзындығын есептеудің бастапқы нүктесі етіп алып, қашықтықты санаудың оң бағыты үшін мүмкін екі бағыттың кез келген бірі алынады. Сонда М нүктесінің орны S=O₁M шамасымен анықталады.

А нүктенің траектория бойындағы орнын әрбір уақыт сәтінде де таба алуымыз үшін, доға ұзындығы S=O₁M және уақыт t-ның әрбір мәніне сәйкес келетін S-тің мәнін беретін бір сарынды, үздіксіз уақыт функциясы берілуі керек.

(2.1)

2.2-сурет

Доға ұзындығы S пен уақыт t-ның арасындағы функциялық тәуелділік (2.1) нүктенің траектория бойымен қозғалуының заңы деп аталады.

2. Координаталық тәсіл.Бізге абсолют қозғалмайтын өстер жүйесіне қатысты М нүктесінің қозғалысын қарастыру керек болсын. Егер осы нүктенің x,y,z уақыт t-ның үздіксіз бірмәнді функциялары болып келсе, яғни:

. (2.3)

онда нүктенің әрбір уақыт сәтіндегі орны толық анықталады.

Сонымен, нүктенің орнын анықтаудың координаттар тәсілінде қандайда бір координаттар жүйесінде оның координаттары уақытқа тәуелді функция ретінде беріледі. (2.3)-теңдеулер нүкте қозғалысының теңдеулері деп аталады. Сонымен қатар, бұл теңдеулерге нүкте траекториясының параметрлік теңдеулері деп қарауға болады. Траектория теңдеуін анықтау үшін (2.3)–теңдеулерден параметр рөлінде тұрған t-ны аластау керек. Сонда траекторияның теңдеуін мынадай екі теңдеу жүйесі түрінде аламыз:

. (2.4)

Мысал. Нүктенің қозғалысы мынадай теңдеулермен берілген:

(а)

Нүкте қозғалысының теңдеулері (а) арқылы, оның траекториясының теңдеуін және нүктенің траектория бойымен қозғалысының заңын анықтау керек. Траектория бойымен есептелетін қашықтық нүктенің бастапқы орнынан бастап саналады.

Шешуі. Нүкте траекториясын табу үшін нүкте қозғалысының заңын өрнектейтін (а) теңдеулерінен параметр ролін атқаратын уақыт ны аластау керек. Ол үшін (а) теңдеулерінің екі жағында квадраттап алып, біріне-бірін қосамыз:

2.3-сурет

немесе . (б)

(б) теңдеуі нүктенің, шеңбер бойымен қозғалатынын көрсетеді (2.3-сурет). Қозғалыс басталардағы уақытты десек, онда нүкте орнында болады. Қашықтықты деп белгілесек, ол мынадай формула арқылы есептеледі:

.

Траектория бойымен қозғалыс заңдылығын анықтаймыз. Уақыт t бойынша x және y-тен туынды аламыз:

.

Осы мәндерді мына теңдікке қоя отырып

,

алатынымыз или . (2)

(2)-теңдеу траектория бойымен нүктенің қозғалыс заңдылығын береді. (1)-теңдеуге сәйкес, =0 болғанда х=0, у=3 болады, яғни нүкте М₀ орнында болады (2.3-сурет), уақыт t өсе бастағанда х өседі, ал у кемиді. Сонымен, доғалық координата S-тің басы М₀ нүктесінде жатыр, ал қозғалыс шеңбер бойымен 2.3-суретте көрсетілген бағытта бағытталады.

2.4-сурет

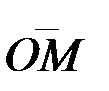3. Векторлық тәсіл.Бұл тәсілде Oxyz координаттар жүйесіне қатысты нүктенің орны = векторымен анықталады (2.4-сурет). Координаттар бас нүктесін және берілген М нүктесін қосатын вектор -ді нүктенің радиус –векторы деп атайды. Қозғалыс кезінде 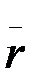-өзінің модулін де, бағытын да өзгертеді. Демек, ол t-ның бір мәнді, үздіксіз, дифференциалданатын функциясы болып келеді. (2.5) өрнегі нүкте қозғалысының векторлық теңдеуі:

. (2.5)